1.5.7. Сходимость в топологических пространствах
Определение. Последовательность точек {xn} топологического пространства Х называется сходящейся к точке x0∈ X, если любая окрестность x0 содержит все точки последовательности, за исключением, быть может, их конечного числа. При этом саму точку x0 называют пределом последовательности и обозначают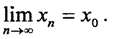 
(Комментарий. В обычной топологии, то есть в метрических пространствах, на прямой пределом последовательности {xn}→ a является точка a, для последовательности xn = a (a - фиксированное число) предел равен a, а последовательность xn = n, n∈N, где N - множество натуральных чисел, не имеет предела. В обычной топологии предел последовательности, если он существует, может быть только один, а в топологических пространствах - несколько. Для пространств, не удовлетворяющих каким-нибудь аксиомам отделимости, свойства пределов могут быть весьма необычными. Так, в тривиальных топологических пространствах любая последовательность точек сходится к каждой точке x∈ X, так как эта точка х имеет только одну окрестность - все множество Х и эта окрестность содержит все точки последовательности. Носитель может содержать конечное или бесконечное число точек x∈X, но топология их не различает.
Рассмотрим прямую с топологией Зарисского. В этой топологии любая точка x∈R является пределом натурального ряда. Действительно, зафиксируем произвольную окрестность U точки x. По определению топологии Зарисского, дополнение U до R состоит из конечного числа точек, то есть в U содержится бесконечное число точек. Поскольку в натуральном ряду бесконечное число точек, отсюда следует, что, начиная с некоторого номера N, все точки n>N лежат в U.
Обычная и дискретная топологии удовлетворяют аксиомам А1 и А2. Однако дискретная топология не очень похожа на обычную. В дискретной топологии открытым является любое множество, то есть любая точка x является сама своей окрестностью Vx. В этом случае в окрестности Vx точки x нет точек, отличных от x. Тогда любая фиксированная точка x может быть пределом только таких последовательностей, у которых, начиная с некоторого N, все члены xn>N равны x.
В произвольном метрическом пространстве точка x0 тогда и только тогда принадлежит замыканию некоторого множества, когда в этом множестве существует последовательность, сходящаяся к x0. В топологическом пространстве справедливо утверждение:
Если последовательность точек множества A топологического пространства (X,τ) сходится к некоторой точке x0∈X, то x0∈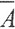
.
Обратное, вообще говоря, не верно.)
Пример. Пусть (X,τ0) - пространство слипшихся точек, где τ0 = {X, ∅}. Носитель может содержать конечное или бесконечное число точек x∈X, но топология их не различает. Множество является единственной окрестностью для всех своих точек, поэтому любая последовательность точек {xn}∈X сходится к любой точке множества согласно определению 1.
|
ПОИСК:
|
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'