1.5.6. Метризуемость

Определение 1. Топологическое пространство T метризуемо, если существует такая метрика ρ на множестве T, что порожденная этой метрикой топология совпадает с исходной топологией пространства T.

Определение 2. Две метрики ρ₁ и ρ₂ на множестве называются эквивалентными, если они порождают на нем одну и ту же топологию.

Пример 1. Показать, что метрики 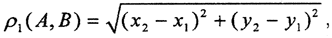, ρ₂(A,B) = max{|y₂-y₁|,|x₂-x₁|} и ρ₃(A,B) = |x₂-x₁|+|y₂-y₁| эквивалентны, то есть задают одну и ту же топологию.

То, что это метрики, было показано ранее. Пусть метрика ρ₁ порождает топологию τ1, ρ₂ - топологию τ₂ и ρ₃ - топологию τ₃. Достаточно показать два равенства. Покажем, что τ₁=τ₂. Рассмотрим множество M, открытое в τ₁ и покажем, что M открыто в τ₂. Возьмем некоторую точку и изобразим шар с центром в этой точке, который целиком лежит в M. Шар в τ₁ - квадрат, шар в τ₂ - круг. А квадрат всегда можно заключить в круг. Тогда M открыто и в τ₂. Аналогично доказывается, что τ₁ = τ₃. А тогда и τ₂ = τ₃.

Теорема 1. Метризуемое топологическое пространство хаусдорфово.

Пусть x,y ∈X, x≠y. Возьмем 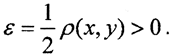Докажем, что U_ε(x)∩U_ε(y) = ∅.

Предположим, что U_ε(x)∩U_ε(y) ≠ ∅, тогда существует z∈U_ε(x)∩U_ε(y), т.е. z∈U_ε(x) и z∈U_ε(y). Тогда, ρ(x,y)≤ρ(x,z)+ρ(z,y)<ε+ε=2ε=ρ(x,y). Получили противоречие. Следовательно, U_ε(x)∩U_ε(y) = ∅.

Пример 2. Топологическое пространство R_→ не является хаусдорфовым, а значит неметризуемо.