1.5.4. Непрерывные отображения

Понятие топологии является минимально необходимым для того, чтобы говорить о непрерывных отображениях в ощем случае. Интуитивно непрерывность есть отсутствие разрывов, то есть близкие точки при непрерывном отображении должны переходить в близкие. Оказывается, для определения понятия близости точек можно обойтись без понятия расстояния. Именно это и есть топологическое определение непрерывного отображения.

Определение 1. Точкой топологического пространства T = (x,τ) называют любой его элемент.

Определение 2.Окрестностью точки в топологическом пространстве называется любое открытое множество, содержащее указанную точку.

Определение 3. Для любого топологического пространства множество A⊂T = (X,τ) называется открытым если каждая точка x∈A имеет окрестность U_x⊂A.

Пусть задано отображение F:X→Y и A⊂X.

Определение 4. Множество F(A):y:=F(x), x⊂A, y⊂Y где называется образом множества А при отображении F.

Определение 5. Для отображения F:X→Y, B⊂Y множество F^-1(B) = {x∈X, F(x)⊂B} называется прообразом множества В при отображении F. Отображение F сюръективно, если F(x) = Y, инъективно, если ∀x₁≠x₂, F(x₁)≠F(x₂) и биективно, если оно сюръективно и инъективно.

(Комментарий. Следует различать прообраз F^-1(B), определяемый для любого отображения F:X→Y, и обратное отображение F^-1:Y→X, существующее только для биективных отображений.

Пусть задано отображение F:X→Y, где X,Y - топологические пространства с топологиями соответственно τ₁ и τ₂. В соответствии с определением окрестности точки в топологическом пространстве, теперь можно дать определение непрерывности отображения F:X→Y в точке.)

Определение 6. Отображение F:X→Y называется непрерывным в точке x₀∈X, если ∀U_F(x0)⊂Y ∃V_x0⊂X точки x₀∈X, такая, что из того, что точка x∈V_x0⊂X, следует, что F(x)⊂U_F(x0) ⊂Y. То есть F(V₀)⊂U_F(x0).

Определение 7. Отображение, непрерывное в каждой точке x множества X, называется непрерывным на X. Если множество X фиксировано, отображения называют просто непрерывными, не указывая X.

Примеры.

1. Для произвольных метрических пространств Х и Y постоянное отображение является непрерывным.
2. Тождественное отображение топологического пространства самого на себя является непрерывным.
3. Непрерывную функцию можно рассматривать как непрерывное отображение из топологического пространства R¹ в топологическое пространство R¹.

Теорема 1 (Критерий непрерывности отображения). Отображение F:X→Y непрерывно если и только если для любого открытого множества U⊂τ₂ пространства Y его прообраз V = F^-1(U) принадлежит τ₁, то есть является открытым множеством топологического пространства X.

Необходимость. Пусть отображение F:X→Y непрерывно. Покажем, что для любого открытого множества U⊂τ₂ пространства Y его прообраз V = F^-1(U) принадлежит τ₁, то есть является открытым множеством топологического пространства X. Выберем открытое множество U⊂Y. U - окрестность каждой своей точки y = F (x), x∈V_x⊂V = F^-1(U). Тогда каждое x∈V_x⊂V⊂X имеет такую окрестность, что F(V_x)⊂U. Так как, по определению, V есть множество всех точек x∈X, таких, что F(x)⊂U, то V_x⊂V. Так как каждое x принадлежит своему V_x, то объединение всех V_x содержит все x. Это значит, что V⊂∪V_x. С другой стороны, все V_x содержатся в V, то есть и их объединение содержится в V, то есть ∪V_x⊂V. Из двух включений и следует равенство V = F^-1(U). Таким образом, V есть объединение открытых множеств V_x, то есть оно само открыто по аксиоме топологии.

Достаточность. Теперь пусть для любого открытого множества U топологического пространства Y (то есть U⊂τ₂) множество V = F^-1(U) открыто в X (то есть принадлежит τ₁). Покажем, что отображение F:X→Y непрерывно. Выберем произвольную окрестность U_F(x) точки F(x) в Y. Это открытое множество, и поэтому V_x = F^-1(U_F(x)) открыто в X по условию. При этом по построению F(V_x) = U_F(x). Итак, для любой окрестности U_F(x) точки F (x) существует окрестность V_x точки x, такая, что F(V_x) содержится в U_F(x), то есть выполнено определение непрерывности.

Определение 8. Отображение топологических пространств называется непрерывным, если прообраз всякого открытого множества открыт.

(Комментарий. Итак, при непрерывном отображении прообраз открытого отображения открыт, а замкнутого замкнут. Для образов при непрерывных отображениях такого рода утверждения, вообще говоря, не имеют место.)

Примеры.

• Непрерывное отображение f: R¹→ R¹, где f(x)=arctgx, отображает бесконечный интервал R = (-∞,∞) в интервал 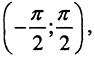т.е. открытое и замкнутое множество - в открытое множество.
• Непрерывное отображение f:R¹→ R¹, где 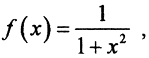отображает открытое и замкнутое множество R = (-∞,∞) в полуинтервал (0; 1], который не является ни открытым, ни замкнутым множеством.
• Тождественное отображение есть пример одновременно открытого и замкнутого отображения.