1.4.6. Топологические свойства метрических пространств

Предел последовательности элементов метрического пространства может быть определен и по-другому без явного обращения к понятию предела числовой последовательности ρ(x_n,x)|_n→∞→0. А это уже "топологический взгляд" на пространства. Введем понятие окрестности элемента пространства. Пусть (X,ρ) - произвольное метрическое пространство.

Определение 1. Открытым шаром с радиусом r и с центром в точке x₀ называется множество точек этого пространства, расстояние до которых меньше r, то есть B(x₀,r) = {x∈X:ρ(x₀,x)<r}.

(Комментарий. Соответствующие переформулировки для нормированных пространств очевидны. В нормированных пространствах B(x₀,r) = {x∈X:|x₀-x||<r}. Окрестностью точки x₀ называется открытый шар с центром в этой точке и радиуса ε. Соответственно, для замкнутого шара 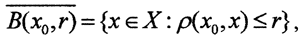, а сфера S(x₀,r) = {x∈X:ρ(x₀,x)=r}.)

Пример. В дискретном пространстве при r<1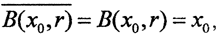 S(x₀,r)=∅ а если r≥1 то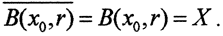

Определение 2. Пусть M - произвольное множество метрического пространства (X,ρ). Точка x₀∈X называется внутренней точкой множества M, если существует окрестность этой точки, целиком входящая в множество M. Совокупность всех внутренних точек множества M называется внутренностью множества M и обозначается int M. Множество, состоящее только из внутренних точек, называется открытым.

Определение 3. Пусть M - произвольное множество метрического пространства (X,ρ). Точка x₀∈X называется внешней точкой множества M, если она является внутренней точкой дополнения, то есть множества X/M. Другими словами, существует окрестность точки x₀, не имеющая с множеством M общих точек.

Определение 4. Пусть M - произвольное множество метрического пространства (X,ρ). Точка x₀∈X называется предельной точкой множества M, если в любой окрестности точки содержится хоть одна точка из множества M, отличная от точки x₀.

(Комментарий. Ясно, что предельная точка множества M может как принадлежать, так и не принадлежать множеству M. У открытого множества существует хоть одна предельная точка, не принадлежащая ему.)

Определение 5. Точка x₀∈X называется изолированной точкой множества M, если существует окрестность точки x₀, не содержащая точек из множества M.

Определение 6. Совокупность предельных и изолированных точек множества M называется точками прикосновения множества M.

Определение 7. Множество M называется дискретным, если оно состоит только из изолированных точек и совершенным, если оно состоит только из предельных точек.

Определение 8. Множество M метрического пространства ρ(X,ρ) называется ограниченным, если существует открытый шар, целиком содержащий множество M.

Определение 9. Диаметром множества M называется число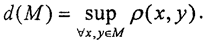

Определение 10. Расстоянием от точки x₀ до множества M называется число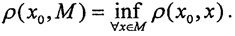

Определение 11. Расстоянием между двумя множествами M и N называется число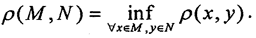

Определение 12. Присоединение к множеству всех его точек прикосновения называется замыканием множества. Замыкание множества M обозначается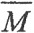

Определение 13. Множество М метрического пространства ρ(X,ρ) называется замкнутым, если оно совпадает со своим замыканием, то есть M = 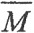. У замкнутого множества существует хоть одна точка, в любой окрестности которой есть точки, не принадлежащие множеству .

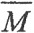Определение 14. Все точки, в любой окрестности которых есть как точки, принадлежащие множеству M, так и не принадлежащие ему, образуют границу множества .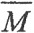

Пример. Может ли расстояние между двумя непересекающимися непустыми замкнутыми множествами равняться нулю?

Да. На числовой прямой возьмём множества A = {2,3,4,...} и 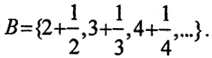На плоскости множества A:y = 0 и B:xy = 1 или B:(x²+1)y = 1.

Теорема 1. Множество метрического пространства открыто тогда и только тогда, когда его дополнение замкнуто.

Необходимость. 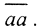Пусть M - открытое множество и множество CM = X/M - открыто. Так как множество CM открыто, то существует хоть одна предельная точка x₀, не принадлежащая множеству CM. Но в любой её окрестности содержится бесконечное число точек из множества CM. Сама же она принадлежит множеству M. Но множество M открыто по условию, то есть точка x₀ внутренняя точка множества M. Но тогда существует окрестность точки x₀, состоящая только из точек множества M. А это противоречит тому, что в любой окрестности точки x₀ содержится бесконечное число точек из множества CM.

Достаточность. 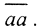Пусть M - замкнутое множество и множество CM = X/M - замкнуто. Так как множество M замкнуто, существует хоть одна точка x₀, в любой окрестности которой есть точки, не принадлежащие множеству 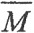. То есть точка x₀ - предельная точка множества CM. Но множество CM тоже замкнуто, то есть содержит все свои предельные точки, то есть точка x₀∈M и x₀∈CM.

Теорема 2 (О замкнутости теоретико-множественных операций над открытыми и замкнутыми множествами).

1. Объединение конечного числа замкнутых множеств - замкнуто.
2. Пересечение любого числа замкнутых множеств - замкнуто.
3. Объединение любого количества открытых множеств есть множество открытое.
4. Пересечение конечного числа открытых множеств есть множество открытое.

1. Пусть множество 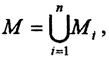причём ∀M_i замкнуты. Покажем, что множество M замкнуто. Рассмотрим m₀ - произвольную предельную точку множества M. Она может принадлежать множеству M, а может и не принадлежать. Но в любой окрестности точки m₀ содержится бесконечное множество точек из множества M. Так как множество есть объединение конечного числа множеств M_i, то, в соответствии с принципом Вейерштрасса, это бесконечное множество точек входит в какое-то из множеств M_i. Но это означает, что точка m₀ есть предельная точка этого множества M_i. Но множество M_i замкнуто, то есть содержит в себе все свои предельные точки, то есть m₀∈M_i. Но точка m₀∈M, то есть множество M содержит в себе все свои предельные точки, то есть оно замкнуто.

2. Пусть множество 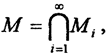причём все множества M замкнуты. Покажем, что множество M замкнуто. Так как множество 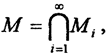то любая предельная точка из множества M принадлежит всем множествам M_i, но они все замкнуты, то есть множество M содержит все свои предельные точки, следовательно, множество M замкнуто.

3. Пусть множество 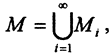причём все множества M_i открыты. Тогда множества CM_i замкнуты. По теореме Де Моргана 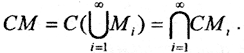Но по второй части теоремы множество 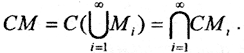замкнуто, а это значит, что множество M открыто.

4. Пусть множество 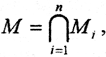причём все множества M_i открыты, то есть множества CM_i замкнуты. По теореме Де Моргана 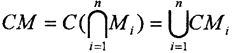замкнуто, а это значит, что множество M открыто.

(Комментарий.

1. Все пространство Х и являются замкнутыми и открытыми множествами одновременно.

2. Пересечение бесконечного числа открытых множеств может и не быть открыто. Рассмотрим, например, в пространстве R¹ пересечение множеств 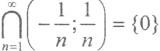. Результат пересечения - одноточечное множество {0} замкнуто, как любое множество, состоящее из конечного числа точек.

3. Объединение бесконечного числа замкнутых множеств может и не быть замкнуто.)

Примеры. 1. В пространстве R¹ множество 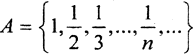обладает следующими свойствами:

• замкнутое, не плотное множество;
• все точки изолированные, и, следовательно, внутренних точек нет;
• точка 0∉A является точкой прикосновения этого множества;
• множество ограничено;
• диаметр множества d(A) = 1;
• множеством внешних точек, то есть дополнением к множеству A, является множество

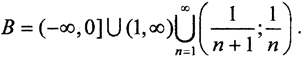
2. Интервал (a,b) ∈R¹ обладает следующими свойствами:

• совершенное, открытое множество так как все его точки внутренние;
• множество точек прикосновения отрезок [a,b];
• изолированных точек нет;
• множество (a,b) ограничено;
• диаметр множества d(a,b) = b-a.
• в любой окрестности точек есть точки, не принадлежащие множеству [a,b].

Теорема 3 (О включении).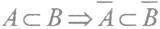

Множество A состоит из предельных A_П и изолированных А_И точек, причём предельные точки могут и не входить в множество. Но 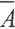=А_П∪А_И и эти множества не пересекаются.

1. Пусть а ∈А_П, то есть в любой её окрестности содержится бесконечное число точек из множества А, но А⊂В, то есть в любой её окрестности содержится бесконечное число точек из множества В, но В⊂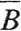, тогда и в этом случае а∈.

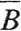2. Пусть а ∈А_И. Тогда а∈А⊂В⊂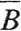, тогда и этом случае а∈.

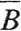Теорема 4 (Об объединении замыканий).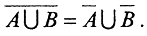

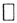
1. Покажем, что 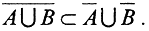Очевидно, что А⊂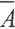, В⊂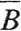, то есть 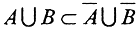но по теореме 2 объединение конечного числа замкнутых множеств - замкнуто, то есть множество А∪В замкнуто, а замыкание замкнутого множества есть замкнутое множество. Стало быть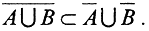

1. Покажем, что 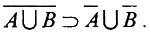. Пусть множество С = 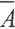∪ 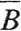и точка с∈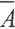∪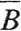, то есть или с∈С_И, или с∈С_П. Если с∈С_И, то 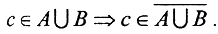Если с∈С_П, то в любой её окрестности содержится бесконечное число точек из множеств А или В, то есть бесконечное число точек из множества 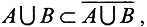стало быть,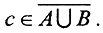

Примеры.1. Показать, что метрическое пространство сепарабельно, если из любой последовательности его точек можно выделить фундаментальную подпоследовательность.

Зафиксируем ε>0 и возьмём любую точку x₁∈X. Точку x₂∈X выберем так, чтобы ρ(x₁,x₂)≥ε. И так далее по правилу ρ(x_n,x_n+1)≥ε. Если этот процесс не закончится, то из получившейся последовательности точек нельзя выделить фундаментальную подпоследовательность, что противоречит условию. Поэтому процесс должен закончиться и после конечного числа шагов мы покроем пространство X конечным числом открытых шаров радиуса ε>0. Взяв 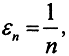рассмотрим множество, состоящее из центров соответствующих наров при каждом n от 1 до бесконечности. Это и будет счётный скелет.

2. Пусть Х - дискретное метрическое пространство с метрикой 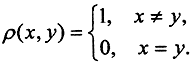Последовательность {x_n}∈X будет фундаментальной и сходящейся в X, если она стационарна, пространство Х является полным пространством, так как любая фундаментальная последовательность сходится. Единственным множеством, всюду плотным в Х является множество А = Х.