1.4.5. Сравнение метрик (норм)

Пусть на носителе метрического пространства X заданы две метрики ρ₁ и ρ₂.

Определение 1. Метрика (норма) ρ₁ сильнее, чем метрика (норма) ρ₂, если из сходимости последовательности {x_n(t)} по метрике ρ₁ следует её сходимость по метрике ρ₂, но существует хоть одна последовательность, которая сходится по метрике ρ₂, но не сходится по метрике ρ₁.

Определение 2. Две метрики (нормы) ρ₁ и ρ₂ эквивалентны, если из сходимости последовательности {x_n(t)} по метрике ρ₁ следует её сходимость по метрике ρ₂ и наоборот.

Определение 2*. Две метрики (нормы) ρ₁ и ρ₂ эквивалентны, если существуют такие α,β>0: αρ₂≤ρ₁≤βρ₂ или αρ₁≤ρ₂≤βρ₁.

Теорема 1. В любых конечномерных пространствах все метрики (нормы) эквивалентны.

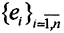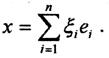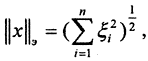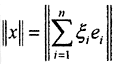Рассмотрим нормированное пространство (X,||x||), dim(X,||x||) = n, система векторов образует базис в нём, то есть ∀x∈X Эвклидова норма а - ещё одна норма в этом пространстве. Оценим её. 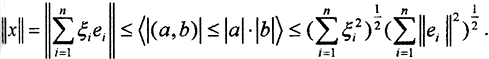Обозначив 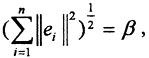получим ||x||≤β||x||_э. Покажем, что ||x||_э в свою очередь подчинена ||x||. Рассмотрим функцию n переменных 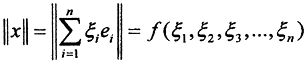на сфере ||x||_э = 1. Она непрерывна, так как 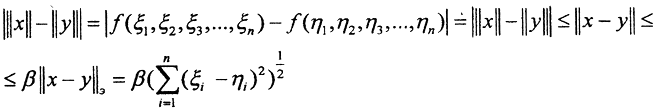и стремится к нулю при (ξ_i-η_i)→0. Единичная сфера 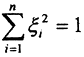- замкнутое ограниченное множество, поэтому на ней, в соответствии с теоремой Вейерштрасса, функция достигает своих точных верхней и нижней граней. То есть на сфере ||x||_э = 1 имеем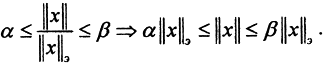

Пример. Доказать, что метрика ρ_С пространства С[0,1] сильнее метрики ρ_C1 пространства C₁[0,1].

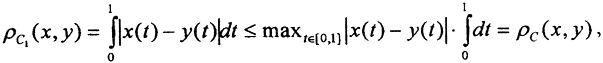
то есть ρ_C не слабее ρ_C1. Теперь укажем последовательность {x_n(t)}, которая сходится по ρ_C1, но не сходится по ρ_C. Эта последовательность стандартный пробник функционального анализа, x_n(t) = tⁿ, y_n(t) = 0. 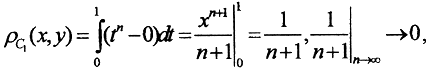а 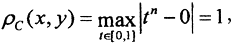то есть эта последовательность сходится по ρ_C1, но не сходится по ρ_C.

(Комментарий. В конечномерных пространствах все метрики (нормы) топологически эквивалентны в следующем смысле: для шара B(х₀,R) радиусом R с центром в точке x₀, построенного на основе одной из норм, можно построить вписанный в него и описанный вокруг него шары, построенные на основе другой нормы (разумеется, другого радиуса). В бесконечномерных пространствах это не так.)

Пример. Покажем, что чебышевская норма, по крайней мере, не слабее гёльдеровской, а дифференциальная не слабее чебышёвской.

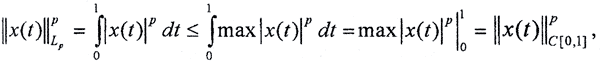
но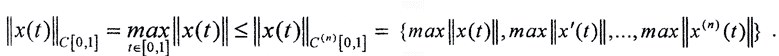

(Комментарий. Будем говорить, что пространство X вложено в пространство Y, если все элементы пространства X принадлежат Y, то есть X⊂ Y, а норма пространства X не слабее нормы пространства Y. Взаимное соотношение между основными пространствами функций: Cⁿ[a,b]⊂ C[a,b]⊂ L₂[a,b], то есть самое "широкое" пространство - пространство суммируемых с квадратом функций L₂[a,b], а самое "узкое" - пространство Cⁿ[a,b]. 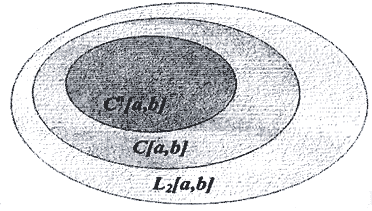В математике используются не только эти, наиболее употребительные, но и другие типы пространств, которые могут быть шире или уже рассмотренных пространств, а могут занимать и некоторое промежуточное положение.)