1.4.4. Сходимость и полнота в метрических пространствах

Определение 1.Последовательность точек x_n метрического пространства сходится по метрике ρ к точке x, если числовая последовательность ρ(x_n,x)|_n→∞→0, то есть ∀ε&362;0 ∃N=N(ε):(n>N⇒ρ(x_n,x)<ε).

(Комментарий. Обозначение используется обычное: {x_n}→x. Таким образом, в метрических пространствах можно использовать теорию числовых последовательностей с естественной метрикой числовой оси ρ(x,y) = |x-y|. Например:)

Теорема 1. Последовательность точек метрического пространства может иметь только один предел.

Пусть последовательность {x_n} имеет два предела, то есть ρ(x_n,a)|_n→∞→0 и ρ(x_n,b)|_n→∞→0. Тогда в неравенстве треугольника для точек a и b, где a ≠b, ρ(a,b) ≤ρ(a,x_n)+ρ(b,x_n). Правая часть стремится к нулю, а левая часть постоянна и отлична от нуля.

Определение 2. Сходимость по норме (метрике) пространства C[a,b] называется равномерной сходимостью. Сходимость по (метрике) норме пространства L₂[a,b] называется сходимостью в среднем.

Определение 3. Последовательность точек x₁, x₂, x₃,... пространства (Х,ρ) называется фундаментальной, если для любого числа ε>0 найдется такое число n₀, что для всех n, m > n₀ выполняется неравенство ρ(x_m, x_n)<ε.

(Комментарий. Ясно, что всякая сходящаяся последовательность является фундаментальной.)

Определение 4. Метрическое пространство, в котором всякая фундаментальная последовательность сходится, называется полным.

(Комментарий. Все стандартные метрические пространства, кроме C_p[a,b], полны, а так как они ещё и нормированы, то все стандартные метрические пространства, кроме C_p[a,b], являются банаховыми.)

Пример 1. Покажем полноту пространства C[a,b].

То, что это метрическое пространство, следует из того, что ρ = max|f-g| = max|(f-φ)+(φ-g)|≤max|f-g|+max|φ-g|. Пусть по метрике пространства C последовательность {f_n(t)}→f(t), то есть ∃N=N(ε):∀n>N max|f_n(t)-f(t)|<ε. Но тогда это условие выполняется и для всех других f_n(t), t∈[a,b], то есть {f_n(t)}→f(t) равномерно (номер N(ε) обеспечивает сходимость для всех f_n(t) сразу). Согласно теореме Вейерштрасса предел равномерно сходящейся последовательности непрерывных функций есть функция непрерывная, то есть функция f_n(t) непрерывна, то есть f(t)∈ C[a,b] и пространство C[a,b] полно.

Теорема 2. Всякое замкнутое подпространство F⊂X полного метрического пространства (X,ρ) является полным пространством.

Пусть последовательность точек x_n∈ F фундаментальна в пространстве (F,ρ). Тогда она будет фундаментальной и в пространстве (X,ρ). А поскольку оно полное, то эта последовательность сходится, 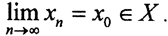. Поскольку множество F замкнуто, то точка x₀∈ F предельная для множества F, что и доказывает полноту пространства F.

(Комментарий. Тот факт, что в полных пространствах понятия замкнутости и полноты для подпространств совпадают, очень важен в приложениях. Однако, надо следить за полнотой исходного пространства.)

Примеры.1. Рассмотрим пространство (X,ρ), где X=(0,1), с метрикой ρ(x₁,x₂) = |x₁-x₂|. Последовательность 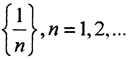фундаментальная, так как 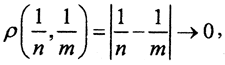, при n,m →∞, но эта последовательность не сходится ни к одному элементу пространства (X,ρ), так как элемент, к которому она сходится, x = 0 не принадлежит пространству X.

2. Такой же пример даёт множество рациональных чисел, рассматриваемое как подмножество числовой оси R¹. Последовательность Бернулли 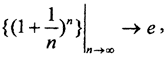, но числа e среди рациональных чисел нет.

3. Рассмотрим множество X=(0,1]. Оно, очевидно, не замкнуто и не полно. Пусть 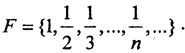. Это множество не замкнуто, хотя состоит из бесконечного числа замкнутых множеств, так как не любая последовательность из этого множества сходится к пределу, ему принадлежащему. Но оно не полно, так как предел этой последовательности равен нулю, которого нет в множестве X.

4. Покажем неполноту пространства C_p[a,b] при p = 1.

1. Сначала покажем, что это метрическое пространство. Ясно, что 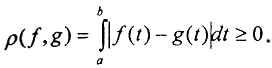. Покажем, что ρ(f,g)=0 ⇔ f=g.

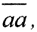
Пусть при каком-то t₀ f(t₀)-g(t₀) ≠0. Тогда в силу непрерывности эта ситуация должна сохраниться и в δ - окрестности точки t₀, то есть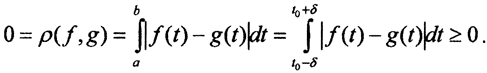

2. Проверим третью аксиому:

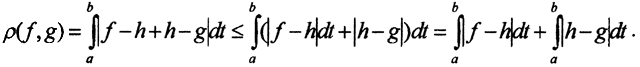
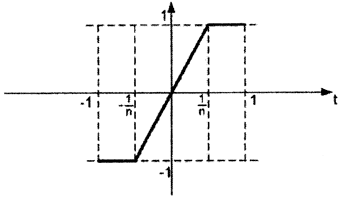
3. Проверим полноту. Пусть последовательность {x_n(t)} →x(t), то есть ∀ε>0∃N=N(ε):(n>N⇒ρ(x_n,x)<ε), t∈[1,-1], где 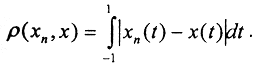Выберем 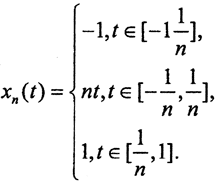как показано на рисунке. Тогда 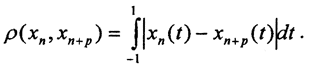. На участке вне сегмента 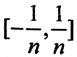функции совпадают и равны единице, то есть 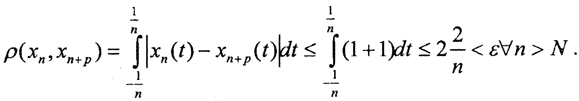. Таким образом, последовательность {x_n(t)} фундаментальна. Ясно, что её пределом будет функция 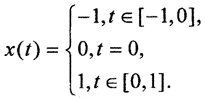В самом деле, 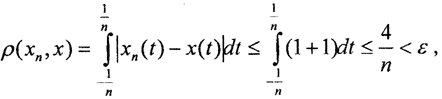то есть последовательность {x_n(t)}→x(t), но функция x(t) разрывна,x(t)∉C₁[1,-1]. Это и означает неполноту пространства C₁[a,b].

(Комментарий. Можно ли пополнить данное метрическое пространство или, более широко, можно ли пополнить любое метрическое пространство? Принципиальный ответ - да. Но для этого иногда нужно идти на коренной пересмотр ситуации. В частности, пространство функций, интегрируемых по Риману, пополнить невозможно, поэтому для того, чтобы сделать пространство C_p[a,b] полным, надо менять процедуру интегрирования. Позже мы построим интеграл Лебега и убедимся, что пространство функций, интегрируемых по Лебегу, уже полно.)

Примеры.1. Верно ли, что последовательность {x_n(t)}→0, если 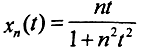в C[0,1] и C₁[0,1]?

В пространстве C[0,1] 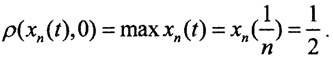. В пространстве C₁[0,1] 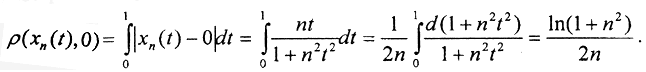. Тогда

2. Верно ли, что последовательность {x_n(t)}→0, если 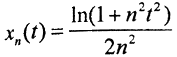в пространстве C¹[0,1]?

3. Показать полноту дискретного метрического пространства.

В дискретном метрическом пространстве все точки изолированные, поэтому фундаментальной последовательностью может быть только стационарная последовательность, которая всегда сходится.

4. Найти предел последовательности 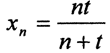в пространстве C[0,2], если он существует.

Необходимым условием сходимости последовательности в пространстве C[a,b] является существование предела x_n при каждом фиксированном t∈[a,b]. Заданная последовательность при заданном t сходится к функции a(t)=t. Данная функция непрерывна.

Проверим, сходится ли последовательность x_n к функции a(t) по норме пространства C[a,b], т.е. равномерно. Вычислим ||x_n-a||. По определению нормы: 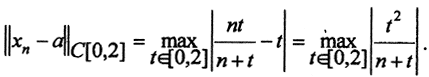Вычислим максимум функции на отрезке [0,2]. Для этого вычислим критические точки: Таким образом, точками возможного экстремума являются точки t₁,t₂. Поскольку t₂ ∉[0,2], то остается лишь точка t₁. Вычислим также значение функции на концах отрезка: 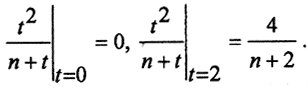То есть 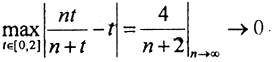Это означает, что последовательность x_n(t) в пространстве C[0,2] сходится к функции a(t)=t.

5. Найти предел последовательности x_n(t) = tⁿ-t²ⁿ в пространстве C[0,1], если он существует.

Последовательность x_n(t)|_{n →∞} →0. Вычислим 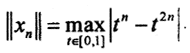Так как (tⁿ-t²ⁿ)' = nt^n-1-2nt^2n-1 = nt^n-1(1-2tⁿ), то nt^n-1(1-2tⁿ) = 0, то есть 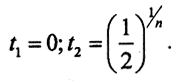Точкой, подозрительной на экстремум, является и точка t₃ = 1. Непосредственной проверкой убеждаемся, что максимум достигается в точке 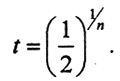Поэтому 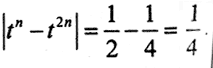Значит, последовательность x_n(t) = tⁿ-t²ⁿ в пространстве C[0,1] не сходится.

6. Сходится ли последовательность в пространстве l₃?

Необходимым условием сходимости последовательности в пространстве l_p, p≥1 является наличие покоординатного предела. Выпишем несколько членов последовательности: 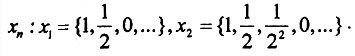Ясно, что последовательность x_n покоординатно сходится к точке 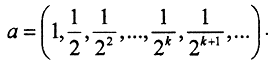Заметим, что a∈l₃, так как 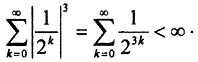Покажем, что последовательность x_n сходится к точке a по норме пространства l₃:

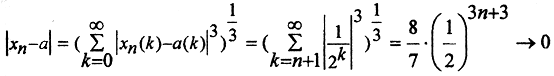
при n→∞.

Следовательно,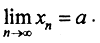

7. Сходится ли последовательность 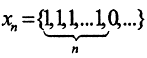в пространстве l₁?

Очевидно, что точка a = (1,1,...,1,...) является покоординатным пределом последовательности, но a∉l₁, так как ряд, составленный из единиц, не является сходящимся. Следовательно, последовательность x_n не имеет предела.

8. Показать, что пространство Rⁿ_p, p≥1, полное.

Пусть последовательность 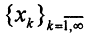фундаментальна в Rⁿ_p. Тогда 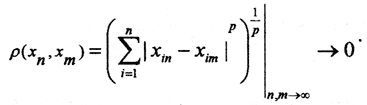Отсюда следует покоординатная сходимость |x_in-x_im|_n,m→∞→0 и, следовательно, фундаментальность числовых последовательностей 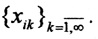Но пространство действительных чисел полное и последовательности 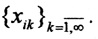сходятся. Следовательно, сходится и последовательность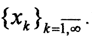

9. Дана последовательность

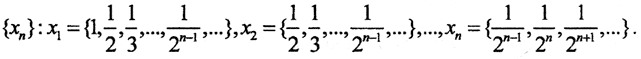
К какой последовательности она сходится покоординатно? Сходится ли она к тому же пределу в метриках пространств l₂, l₁, l?

Ясно, что покоординатно последовательность {x_n} сходится к нулю. В соответствующих метриках она ведет себя так:

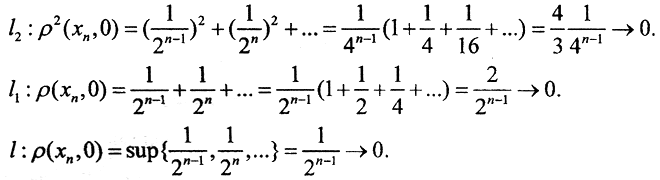
(Комментарий. Из предыдущего примера не следует, что всегда из покоординатной сходимости следует сходимость по метрике соответствующего пространства.)

10. Дана последовательность {x_n}:x₁ = {1,1,...,1,...}, x₂ = {0,1,...},..., x_n = {0,0,...,0,1,...} Ясно, что покоординатно последовательность {x_n} сходится к нулю. Однако в пространстве l: ρ(x_n,0)=sup{1,1,...}=1≠0

11. Множество всех многочленов в пространстве C[a,b] не является замкнутым, так как, например, функцию можно приблизить частичными суммами ряда Тейлора, которые являются алгебраическими многочленами. Следовательно, множество всех многочленов в пространстве не содержит всех предельных точек, и, значит, оно не является замкнутым.