1.4.3. Стандартные метрические пространства

1. Rⁿ_p - n-мерное арифметическое пространство с радикальной метрикой. При p = 1 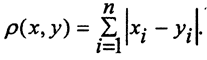(проверка неравенства треугольника: |x_i-y_i|=|(x_i-z_i)+(z_i-y_i)|≤|x_i-z_i|+|z_i-y_i|.) При p = 2 метрику 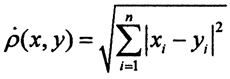называют эвклидовой, а пространство Rⁿ₂ - арифметическим n-мерным пространством. Это пространство в линейной алгебре обозначается Rⁿ.
2. Rⁿ - n-мерное арифметическое пространство с супремальной метрикой.
3. l_p - пространство ограниченных последовательностей с радикальной метрикой 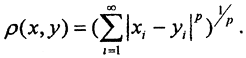. При p = 2 это такие последовательности, сумма квадратов элементов которых конечна (то есть ряд сходится). Эту сумму квадратов, т.е. сумму ряда, назовем квадратом длины вектора. Операции сложения и умножения на число определим как для конечномерных векторов-столбцов, то есть поэлементно (координатное гильбертово пространство).
4. l_∞ или l, или m - пространство ограниченных последовательностей с супремальной метрикой.
5. C_p[a,b] - пространство непрерывных функций с радикальной метрикой. Его пополнение - L_p[a,b] - лебегово пространство. Метрика пространства Лебега 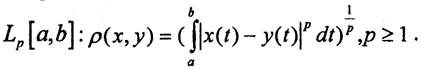При p = 2 пространство L_p[a,b] - гильбертово и обозначается как H₂.
6. C[a,b] - пространство непрерывных функций с супремальной метрикой (чебышевское).
7. Cⁿ[a,b], или C⁽ⁿ⁾[a,b] - пространство раз непрерывно дифференцируемых функций с супремальной метрикой. Такая метрика называется дифференциальной и вычисляется по формуле
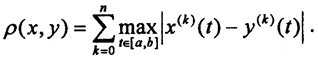
8. Cⁿ_p[a,b] - пространства непрерывно дифференцируемых функций с радикальной метрикой. Их пополнение Wⁿ_p[a,b] - пространства Соболева. Метрика пространств Соболева 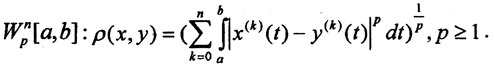При p = 2 пространство Wⁿ₂[a,b] гильбертово и обозначается как Hⁿ.

Пример 1. На плоскости R² для точек A(x₁, y₁) и B(x₂, y₂) определим расстояние тремя различными способами и покажем, что введенные расстояния являются метриками, то есть проверим выполнимость аксиом.

1.Метрика 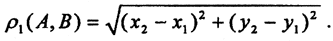. Это евклидова метрика при p = 2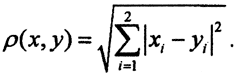

Первые аксиомы очевидны. Проверим третью аксиому. Рассмотрим точки A(x₁, y₁), B(x₂, y₂) и C(x₃, y₃) докажем следующее неравенство:

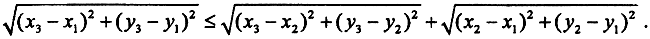
Возведем это неравенство в квадрат:

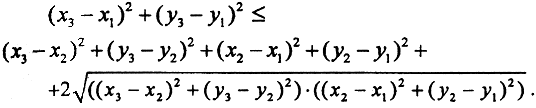
Так как (x₃-x₁)²≤(x₃-x₂)²+(x₂-x₁)² и (y₃-y₁)²≤(y₃-y₂)²+(y₂-y₁)² (поскольку (b-a)²)≤b²+a²) и выражение 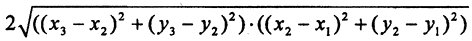неотрицательно, то неравенство является верным.

2. Метрика ρ₂(A,B) = max{|y₂-y₁|, |x₂-x₁|}. Это двумерное арифметическое пространство с супремальной метрикой. Первые аксиомы очевидны. Проверим третью аксиому.

Рассмотрим точки A(x₁, y₁), B(x₂, y₂) и C(x₃, y₃) докажем следующее неравенство: ρ₂(A,C)≤ρ₂(A,B)+ρ₂(C,B)

|y₁-y₂|≤|y₃-y₁|+|y₃-y₂|≤ max{|y₃-y₁|, |x₃-x₁|}+max{|y₃-y₂|, |x₃-x₂|},

|x₁-x₂|≤|x₃-x₁|+|x₃-x₂|≤ max{|y₃-y₁|, |x₃-x₁|}+max{|y₃-y₂|, |x₃-x₂|}.

Тогда и

max{|y₂-y₁|, |x₂-x₁|}≤max{|y₃-y₁|, |x₃-x₁|}+max{|y₃-y₂|, |x₃-x₂|}.

3. Метрика ρ₃(A,B) = |x₂-x₁|+|y₂-y₁|. Это двумерное арифметическое пространство с радикальной метрикой при p = 1. Такую метрику называют манхеттенской. Кратчайшее расстояние между точками A(x₁,y₁) и B(x₂,y₂) будет определяться формулой ρ₃(A,B) = |x₂-x₁|+|y₂-y₁|. Первые аксиомы очевидны. Проверим третью аксиому. Рассмотрим точки A(x₁,y₁), B(x₂,y₂), C(x₃,y₃). Неравенство |x₃-x₁|+|y₃-y₁|≤|x₃-x₂|+|x₂-x₁|+|y₃-y₂|+|y₂-y₁| очевидно.

(Комментарий. 1. Понятие пополнения употреблено впрок и будет определено позднее.

Для стандартных метрических пространств это так, так что все вышеприведённые примеры являются одновременно и примерами стандартных норм с геометрией, отличной от эвклидовой. Единичные шары в этих метриках изображены в примере 3.)

Пример 2. Покажем, что ρ = arctg|x-y| является метрикой. Выполнение первых двух аксиом метрики очевидно. Чтобы проверить третью, то есть arctg|x-z+z-y|≤arctg|x-z|+arctg|z-y|, докажем, что для любых α,β ≥0имеет место неравенство arctg(α+β)≤arctgα+arctgβ.

Для этого зафиксируем β и рассмотрим функцию f(α) = arctgα+arctgβ-arctg(α+β). Так как f(0) = 0, а f'(α)>0, то f(α) - возрастающая функция. Однако метрика p = arctg|x-y| при p = 0 не будет нормой, так как arctgλx≠|λ|arctgx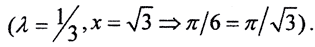

Пример 3. Рассмотрим пространство R²_p. Положив y = 0, а ρ = 1, мы получим единичную сферу в пространстве R²_p.

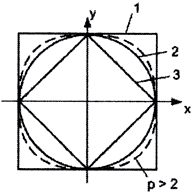
При p = 1 уравнение этой сферы имеет вид ||x||₁ = |x|+|y| = 1, и такая метрика называется октаэдрической, потому что единичной сферой в трёхмерном случае ||x||₁ = |x|+|y|+|z| = 1 будет октаэдр.

При p = 2 уравнение этой сферы имеет вид 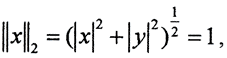и такая метрика называется евклидовой (сферической), потому что единичной сферой в трёхмерном случае будет обычная сфера.

Чебышёвская (кубическая) метрика: ||x||_∞ = max{|x|,|y|}, потому что единичной сферой в трёхмерном случае ||x||_∞ = max{|x|,|y|,|z|} = 1 будет куб.

На рисунке: 1 - единичная сфера с чебышёвской (кубической) метрикой; 2 - единичная сфера с евклидовой (сферической) метрикой; 3 - единичная сфера с октаэдрической метрикой. Случай p>2 изображен пунктиром. При p→∞ единичная сфера с гёльдеровской группой метрик стремится к чебышёвской.

Примеры.

1. Пространство изолированных точек (дискретное пространство): 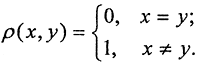Здесь X - любое непустое множество. Первые две аксиомы очевидны. Проверим третью.

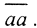
Пусть неверно, что ρ(x,y)≤ρ(x,z)+ρ(z,y). Тогда ρ(x,y) = 1.⇒x ≠y. Но тогда ρ(x,z)+ρ(z,y) = 0, то есть x=y.

2. Ограниченные последовательности 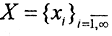с метрикой 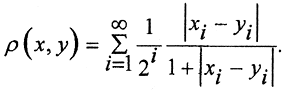Проверим третью аксиому.

Рассмотрим возрастающую функцию 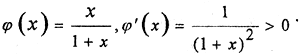Так как |α+β|≤|α|+|β|, то φ(|α+β|)≤φ(|α|)+φ(|β|), то есть 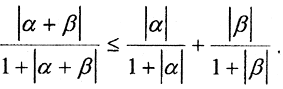Пусть α = x_i-z_i, β = z_i-y_i, тогда α+β = x_i-y_i. Теперь 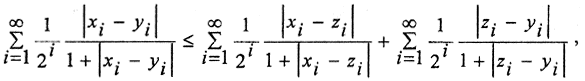или ρ(x,y)≤ρ(x,z)+ρ(z,y).

(Комментарий. Пусть ρ(x,y) - метрика на носителе X. Тогда 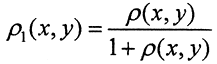- тоже метрика на носителе X. Это позволяет дать следующее определение: )

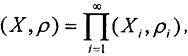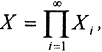Определение. Пусть {(X₁,ρ₁), (X₂,ρ₂),... (X_n,ρ_n)} - последовательность метрических пространств. Прямым (декартовым) произведением этих метрических пространств называется пара где а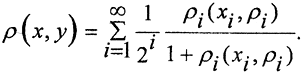

3. Покажем, что пара (N,ρ) - метрическое пространство, если на множестве натуральных чисел n,m ∈N метрика задана так: 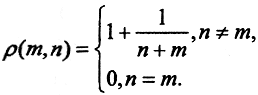Неравенство треугольника для несовпадающих точек m,n,p очевидно: .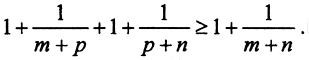

В этой метрике при m<n₁<n₂ ρ(m, n₁)>ρ(m, n₂) то есть натуральные числа, чем дальше они расположены на числовой оси, тем ближе по метрике ρ.

4.l_p - пространство ограниченных последовательностей с радикальной метрикой 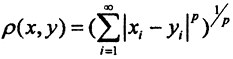при p≠2 не эвклидово.

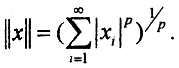
Пусть x = {1,1,0,...}, y = {1,-1,0,...}.

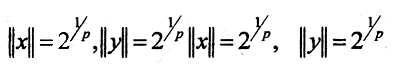
Ясно, что равенство параллелограмма не выполнено при p≠2.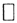

5. Покажем, что пространство C[0,1] не гильбертово.

Пространство C[0,1] полное нормированное пространство, то есть банахово. (Полноту покажем в следующем пункте.) Уже отмечалось, что норма порождается скалярным произведением, если и только если выполняется равенство параллелограмма ||x+y||²+||x-y||² = 2(||x||²+||y||²). Пусть x(t) = 1, y(t) = t. Тогда, вычисляя норму в пространстве C[0,1], сразу получим ||t+1||²+||t-1||² = 2²+1² ≠2(1²+1²).

6. Будет ли нормированным пространством линейное пространство непрерывно дифференцируемых функций, если на нём в качестве нормы использовать норму пространства непрерывных функций C[0,1]?

Да. Проверим аксиоматику:

1)||x(t)||_[a,b] = max _t∈[a,b]|x(t)|≥0, причём ||x(t)||_[a,b] = max|x(t)| = 0⇔x(t)=0 ∀ t∈[a,b],

2)||λx(t)||_[a,b] = max|λx(t)| = max(|λ||x(t)|) = |λ|max||x(t)||_[a,b] = |λ|||x(t)||_[a,b],

3)||x(t)+y(t)||_t∈[a,b] = max_t∈[a,b]|x(t)+y(t)|≤ max_t∈[a,b](|x(t)|+|y(t)|)≤ max_t∈[a,b]|x(t)|+max_t∈[a,b]|y(t)| = ||x(t)||_t∈[a,b]+||y(t)||_t∈[a,b].

7. Будет ли нормированным пространством линейное пространство непрерывно дифференцируемых функций, если на нём в качестве нормы использовать норму ||x(t)||_t∈[a,b] = max_t∈[a,b]|x'(t)|?

Нет, так как не выполняется первая аксиома нормы: ||x(t)||_t∈[a,b] = max_t∈[a,b]|x'(t)| = 0 ⇒x(t)=c, где с - произвольная константа.

8. Доказать, что подпространство B₁ банахова пространства B является банаховым пространством.

Пусть последовательность {x_n} = {x₁, x₂, ..., x_n, ...} фундаментальна в подпространстве B₁ банахова пространства B (нормы, естественно, одинаковы). Эта последовательность является фундаментальной и в B, так как B₁ - подпространство. Но B - банахово пространство, то есть {x_n}→x∈B. Так как B₁ - подпространство, то по определению подпространства оно замкнуто, следовательно, x∈B₁. Таким образом, произвольная фундаментальная последовательность в подпространстве B₁ сходится к x∈B₁, а это и значит, что B₁ банахово пространство по определению.