1.4.7. Плотность и сепарабельность

Определение 1. Множество M называется плотным в множестве N, если N⊂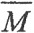, то есть любой элемент из множества N есть предельная точка множества M.

Определение 2. Если множество N = X, то есть совпадает со всем носителем метрического пространства X, то множество M называется всюду плотным в множестве X.

(Комментарий. Всюду плотность означает, что любой элемент из множества X есть предел последовательности элементов из множества M, то есть ∀x ∈X в любой, сколь угодно малой окрестности точки найдутся точки из множества M, то есть все точки x ∈X есть точки прикосновения множества M, то есть замыкание множества M совпадает со всем пространством.)

Определение 3. Пусть M - произвольное множество метрического пространства (X,ρ). Множество M называется нигде не плотным в множестве X, если замыкание множества M не содержит ни одного непустого шара множества X, то есть в каждом открытом шаре B⊂X найдётся шар B'⊂B, не содержащий точек из множества M.

Примеры.

• Множество рациональных чисел всюду плотно на действительной оси, то есть любое действительное число является либо рациональным числом, либо пределом последовательности рациональных чисел.
• Множество целых чисел Z нигде не плотно на действительной оси X, так как замыкание множества Z совпадает самим множеством Z и оно не содержит ни одного непустого шара множества X.
• В пространстве C[a,b] плотны линейные многообразия тригонометрических и алгебраических полиномов.
• Любая изолированная точка в любом пространстве есть нигде не плотное множество.
• Любое подмножество нигде не плотного множества нигде не плотно.
• Объединение конечного числа нигде не плотных множеств нигде не плотно.
• Объединение счётного числа нигде не плотных множеств уже не нигде не плотно. Оно может быть даже всюду плотно. Множество рациональных чисел счётное всюду плотное множество на действительной оси, но оно есть объединение счётного числа изолированных точек.

Определение 4. Метрическое пространство (X,ρ) сепарабельно, если в нём существует счётное всюду плотное множество "счётный скелет".

(Комментарий. Сепарабельность означает, что в пространстве (X,ρ) существует последовательность {x_n}, такая, что ∀x ∈X из неё можно выделить (separate (лат) - выделять) подпоследовательность {x_nk}, сходящуюся к элементу х, или, что то же самое, ∃{x_n}∈X:(∀ε>0)^(∀x ∈X)∃x_nk∈{x_n}: ρ(x,x_nk)<ε.)

Примеры.

• Эвклидово пространство Rⁿ₂ сепарабельно. Счётный скелет в нём - множество точек с рациональными координатами.
• Дискретное метрическое пространство, состоящее из счётного числа точек, сепарабельно, потому, что, по определению, множество называется всюду плотным, если его замыкание совпадает со всем пространством. Здесь счётный скелет совпадает со всем пространством, а других точек нет.
• Пространство C[a,b] сепарабельно, так как счётный скелет здесь образует множество полиномов с рациональными коэффициентами, а по теореме Вейерштрасса любую функцию из C[a,b] можно сколь угодно точно приблизить суммой таких полиномов.
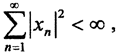• Пространство l₂ сепарабельно. Рассмотрим множество L всех последовательностей с рациональными членами, у которых только конечное, для каждого своё, число членов не равно нулю, а остальные члены нулевые. Это множество счётно, как объединение счётного числа счётных множеств. Покажем, что множество L образует счётный скелет в l₂. Пусть последовательность {x_n}∈l₂. Так как то есть ряд сходится, то 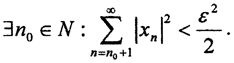Так как множество рациональных чисел Q всюду плотно на числовой оси, то 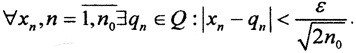Нормировочный множитель выбран для удобства и в силу произвольности ε. Рассмотрим последовательность {q_n}∈L, члены которой при n>n+1 равны нулю. Тогда расстояние между x∈l₂ и q∈Q 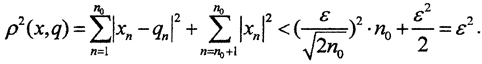Это значит, что ρ(x,q)<ε и замыкание L совпадает с l₂, то есть множество L образует счётный скелет в l₂.
• Пространство l(m) не сепарабельно. Пусть x∈m, x = {ξ_i}, ∀ξ_i = 0,1. Тогда x - двоичное представление числа, а множество всех таких чисел имеет мощность континуума. В метрике l ρ(x,y) = max|x-y| = 1. Пусть пространство сепарабельно, то есть в нём существует счётное всюду плотное множество s - счётный скелет. Опишем вокруг каждого элемента из s шар B(x,ε), 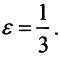Всего элементов - счётное множество, то есть и шаров - счётное множество, а множество элементов в пространстве l имеет мощность континуума, то есть по крайней мере в одном из шаров должно находиться по крайней мере два элемента из пространства l(принцип Вейерштрасса). Пусть x₀ - центр такого шара. Тогда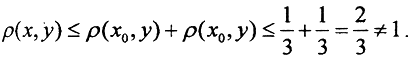

Теорема 1. Во всяком сепарабельном предгильбертовом пространстве X существует ортонормированный базис из конечного или счётного числа элементов.

Пусть 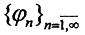счётный скелет пространства X. Выбросив из него элементы, которые можно представить в виде линейной комбинации оставшихся элементов, получим полную линейно независимую систему функций, ортонормируя которую и получим базис.