1.3. Нормированные пространства

Заметим, что эвклидова норма 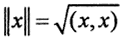обладает очевидными свойствами:

1. ||x ≥0||, ||x||=0⇔ x=0;
2. ||αx||=|α|*||x|| для любого x∈X и любого числа α;
3. ||x+y||≤||x||+||y|| для любых x,y ∈ L (неравенство треугольника).

Неотрицательность и положительная однородность функционала 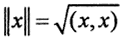очевидны. Покажем неравенство треугольника:

Приняв эти свойства за аксиомы, получим следующее

Определение 1.Говорят, что на линейной структуре (L,F,+,*) задана норма его элементов, если указан функционал, ставящий в соответствие этим элементам действительное число, удовлетворяющее аксиомам 1-3. Пара (L,||x||) называется нормированным пространством.

Определение 2.Полное бесконечномерное нормированное пространство называется банаховым.

Пример. Доказать, что ∀ x,y ∈X, где X - нормированное пространство, выполняется неравенство ||x||≤max{||x+y||,||x-y||}.

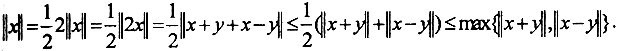
(Комментарий. 1. Ясно, что любое эвклидово пространство нормировано. Обратное, вообще говоря, неверно нормированные пространства не обязаны быть эвклидовыми.

2. Обратим внимание, что и гильбертовы пространства как полные бесконечномерные эвклидовы пространства и банаховы пространства как полные бесконечномерные нормированные пространства построены на линейных структурах. Сейчас мы начнём строить пространства на произвольных носителях.)