1.2.4. Полнота системы векторов в смысле Стеклова

Теорема 1.(О линейной независимости ортогональных векторов). Пусть 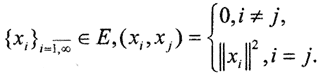Тогда система векторов линейно независима.

Составим линейную комбинацию ∑λ_ix_i=0 и рассмотрим скалярное произведение (x_j, ∑λ_ix_i)=λ_j||x_j||²=0, но ||x_j||²≠0⇒λ_j=0.

Определение 1.Система векторов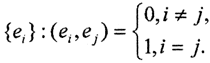 или (e_i,e_j)=δ_ij - символ Кронекера, называется ортонормированной (ОНС).

Определение 2.Для произвольного элемента x произвольного бесконечномерного евклидова пространства и произвольной ортонормированной системы элементов 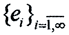рядом Фурье элемента x по системе 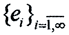называется формально составленная бесконечная сумма (ряд) вида 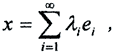, в которой действительные числа λ_i называются коэффициентами Фурье элемента x по системе 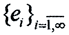, где λ_i=(x,e_i).

Комментарий. (Естественно, возникает вопрос о сходимости этого ряда. Для исследования этого вопроса зафиксируем произвольный номер n и выясним, что отличает n-ю частичную сумму ряда Фурье от любой другой линейной комбинации 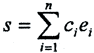первых n элементов ортонормированной системы .)

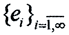Теорема 2.Для любого фиксированного номера n среди всех сумм вида 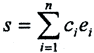наименьшее отклонение от элемента x по норме данного евклидова пространства имеет n-я частичная сумма ряда Фурье элементa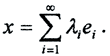

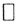
Учитывая ортонормированность системы и определение коэффициента Фурье, можно записать

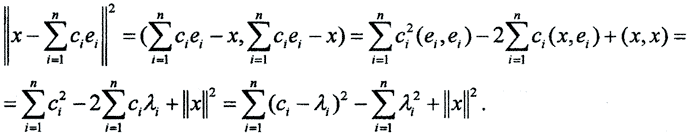
Минимум этого выражения достигается при c_i=λ_i, так как при этом всегда неотрицательная первая сумма в правой части обращается в нуль, а остальные слагаемые от c_i не зависят.

Пример. Рассмотрим тригонометрическую систему

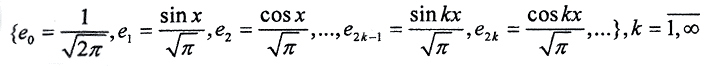
в пространстве всех интегрируемых по Риману функций f(x) на сегменте [-π,π]. Легко проверить, что это ОНС, и тогда Ряд Фурье функции f(x) имеет вид 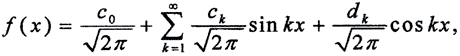где .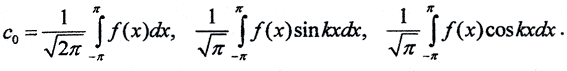

Комментарий. (Тригонометрический ряд Фурье обычно записывают в виде 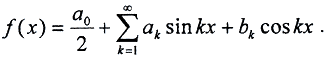Тогда )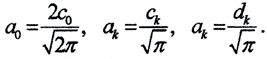

Произвольная ОНС в бесконечномерном эвклидовом пространстве без дополнительных предположений, вообще говоря, не является базисом этого пространства. На интуитивном уровне, не давая строгих определений, опишем суть дела. В произвольном бесконечномерном эвклидовом пространстве E рассмотрим ОНС 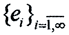, где (e_i,e_j)=δ_ij - символ Кронекера. Пусть M - подпространство эвклидова пространства, а k=M^⊥ - подпространство, ортогональное к M, такое, что эвклидово пространство E=M+M^⊥. Проекция вектора x∈E на подпространство M - вектор 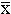∈M, где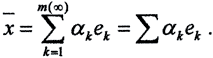

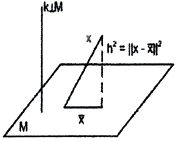
Мы будем искать те значения коэффициентов разложения α_k, при которых невязка (квадрат невязки) h²=||x-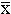||² будет минимальна:

h²=||x-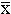||²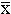=(x-,x-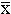)=(x-∑α_ke_k,x-∑α_ke_k)=(x,x)-2∑α_k(x,e_k)+(∑α_ke_k,∑α_ke_k)=||x||²-2∑α_k(x,e_k)+∑α_k²+∑(x,e_k)²-∑(x,e_k)²=||x||²+∑(α_k-(x,e_k))²-∑(x,e_k)².

Ясно, что это выражение будет принимать минимальное значение при α_k=0, что тривиально, и при α_k=(x,e_k). Тогда ρ_min=||x||²-∑α_k²≥0. Отсюда получаем неравенство Бесселя ∑α_k²&38804;||x||². При ρ=0 ортонормированная система векторов (ОНС) называется полной ортонормированной системой в смысле Стеклова (ПОНС). Отсюда можно получить равенство Стеклова - Парсеваля ∑α_k²=||x||² - "теорему Пифагора" для полных в смысле Стеклова бесконечномерных эвклидовых пространств. Теперь следовало бы доказать, что для того, чтобы любой вектор пространства можно было единственным образом представить в виде сходящегося к нему ряда Фурье, необходимо и достаточно выполнение равенства Стеклова-Парсеваля. Система векторов 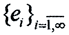ОНБ образует?система векторов 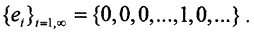Рассмотрим для 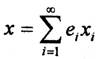частичную сумму ря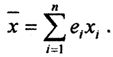да Тогда 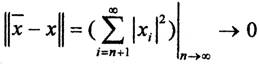как хвост сходящегося ряда. Таким образом, система векторов является ПОНС и образует ОНБ.

Пример. Тригонометрическая система

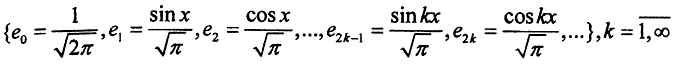
в пространстве всех интегрируемых по Риману функций f(x) на сегменте [-π,π] является ПОНС и образует ОНБ.

Теорема 3 (Грамм Шмидт об ортогонализации).Пусть 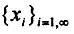- линейно независимая система векторов эвклидова пространства E. Тогда в пространстве E существует ОНС .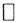

Построим эту ортонормированную систему векторов. Обозначим 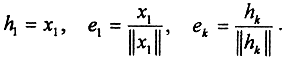Построим h₂=x₂+α₁e₁ и выберем α₁ так, чтобы e₁ ⊥ h₂, то есть (x₂+α₁e₁,e₁)=(x₂,e₁)+α₁(e₁,e₁)⇒α₁=-(x₂,e₁). Тогда h₂=x₂-(x₂,e₁)e₁. Построим вектор h₃=x₃+α₂e₁+α₃e₂ таким образом, чтобы скалярные произведения обратились в ноль: 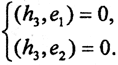Тогда (h₃,e₁)=(x₃+α₂e₁+α₃e₂,e₁)=(x₃,e₁)+α₂(e₁,e₁)+α₃(e₂,e₁), а α₂=-(x₃,e₁) и α₃=-(x₃,e₂). Продолжая процедуру, получим 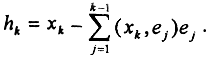Эту формулу следует доказать методом матиндукции.

Примеры. 1. Любую конечномерную ортогональную систему векторов можно дополнить до ОНБ. Дополнить совокупность векторов 1) a₁={1,-1,1}, a₂={-1,1,2} 2) 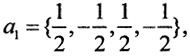, 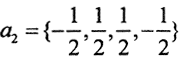до ОНБ.

2. Найти ортонормированный базис линейной оболочки: x₁={1,1,-1,-2}, x₂={-2,1,5,11}, x₃={0,3,3,7}, x₄={3,-3,-3,-9}.

3. Ортогонализировать векторы {x₁=1, x₂=t, x₃=t²} в пространстве E[0,1], показав их линейную независимость. (Совокупность функций {x_k(t)}_k=1,n - линейно независима ∀ t∈ [a,b], если и только если её вронскиан

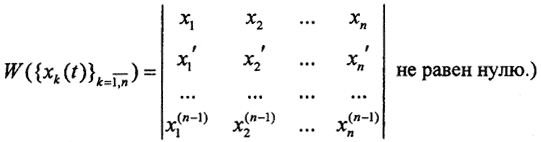
не равен нулю.)

Комментарий. Ортогонализированная система векторов {x_i}={1,t,t²,t³}, 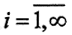в E[-1,1] называется полиномами Лежандра: 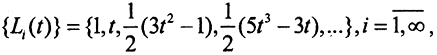которые появляются при решении многих задач математической физики.