1.2.3. Полнота в смысле Фреше

Определение 1.Последовательность точек x_n пространства со скалярным произведением сходится по норме к точке x, принадлежащей пространству, если числовая последовательность ||x_n-x|||_n→∞→0, то есть ∀ε>0 ∃ N=N(ε): (n>N ⇒||x_n-x||<ε). Обозначение используется обычное: {x_n}→x.

Определение 2.Пусть множество M⊂E. Множество 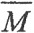⊂E называется замыканием множества M, если для любой точки x∈ 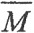существует последовательность не обязательно различных точек из множества M, сходящихся к точке х.

Определение 3.Множество называется замкнутым, если оно совпадает со своим замыканием, то есть M=.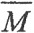

Комментарий. (В определении допускаются стационарные, начиная с некоторого номера, последовательности. Поэтому множество, состоящее из любого конечного числа изолированных точек, замкнуто. Позже мы рассмотрим этот вопрос подробнее.)

Определение 4.Последовательность точек x_n эвклидова пространства E называется фундаментальной, если ∀ε>0 ∃n₀=n₀(ε):(∀n,m>n₀⇒||x_n-x_m||<ε).

Определение 4^*.Последовательность точек x_n эвклидова пространства E называется фундаментальной, если ∀ε>0 ∃n₀=n₀(ε):(∀n>n₀, ∀p∈N ⇒||x_n-x_n+p||<ε).

Теорема 1.Последовательность точек x_n эвклидова пространства E фундаментальна, если она сходится по норме к точке x, принадлежащей пространству.

Пусть {x_n}→x. Тогда 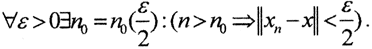Выберем произвольные n,m>n₀. Тогда из неравенства треугольника имеем ||x_n-x_m||≤||x_n-x||+||x_m-x||<ε.

Комментарий. (Обратное, вообще говоря, неверно.)

Определение 5.Эвклидово пространство E называется полным (в смысле Фреше), если всякая его фундаментальная последовательность сходится.

Определение 6.Полное бесконечномерное эвклидово пространство называется гильбертовым.