
1.2.2. Геометрия пространств со скалярным произведением
Теорема 1. (Неравенство Буняковского-Коши или неравенство Шварца).
1. Действительный случай: (x,y) ≤|(x,y)| ≤||x||*||y||.
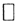
Пусть x,y∈E, z=x+λy ∈E, (z,z)≥0, то есть (z,z)=(x+λy,x+λy)=(x,x)+2λ(x,y)+λ2(y,y)≥0. Это квадратное неравенство относительно λ выполнено ∀x,y ∈E, если его дискриминант D≤0, то есть (x,y)2-||x||2||y||2≤0 ⇒ |(x,y)|≤||x||*||y||.
2. Комплексный случай: |(x,y)|≤||x||*||y||.
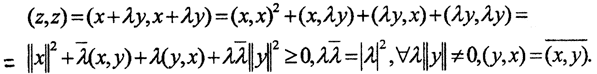
Пусть 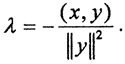 Подставив его в неравенство, получим
Подставив его в неравенство, получим 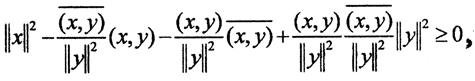 то есть
то есть 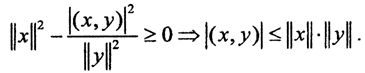
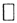
Теорема 2. (Неравенство Минковского или неравенство треугольника): ||x+y||≤||x||+||y||.
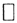
. Для действительного случая ||x+y||2=(x+y,x+y)=||x||2+2(x,y)+||y||2, но (x,y)≤|(x,y)|≤||x||*||y||. Тогда ||x+y||2≤(||x||+||y||)2.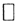
Определение 1. Пусть x,y ∈ E. Косинус угла между элементами x и y определяется равенством 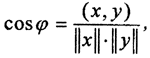 , где φ∈[0,π].
, где φ∈[0,π].
Комментарий. (Два элемента произвольного евклидова пространства называются ортогональными, если скалярное произведение этих элементов равно нулю. Нуль - вектор ортогонален любому ненулевому вектору.)
Теорема 3. (Равенство параллелограмма):
||x+y||2+||x-y||2=2(||x||2+||y||2).
||x+y||2+||x-y||2=(x+y,x+y)+(x-y,x-y)=(x,x)+(x,y)+(y,x)+(y,y)+(x,x)-(x,y)-(y,x)+(y,y)=2(||x||2+||y||2).
Следствие: ||x+y||2+||x-y||2=4(x,y).
Комментарий. (В параллелограмме, построенном на векторах x,y∈E3, где E3 - обычное геометрическое пространство, диагонали задаются векторами x+y и x-y, а, как учат в восьмом классе, сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон. Равенство параллелограмма является, в некотором смысле, бесконечномерным обобщением этого факта. В неэвклидовых пространствах равенство параллелограмма не выполняется.)
Пример. В линейном пространстве последовательностей комплексных чисел x={x1,x2,...,xi,...}, 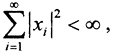 скалярное произведение можно ввести следующим образом:
скалярное произведение можно ввести следующим образом: 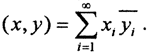 . Аксиомы скалярного произведения очевидны. Ряды
. Аксиомы скалярного произведения очевидны. Ряды 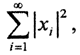
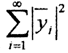 сходятся по условию, а из неравенства Буняковского-Коши
сходятся по условию, а из неравенства Буняковского-Коши 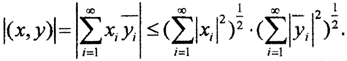
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'