
1.2.1. Определения и примеры
Определение 1.Пусть задана линейная структура (L, F, +, ·), где x,y,z,...∈L, поле F совпадает или с полем действительных чисел R или с полем комплексных чисел C. Говорят, что на линейной структуре (L, F, +, ·) задано скалярное произведение (x,y), любым элементам носителя x,y ставится в соответствие действительное или комплексное число, удовлетворяющее аксиомам (легко доказываемым для обычных геометрических векторов):
- ∀ x,y,z ∈L и ∀ λi∈C (λ1x+λ2y,z)=λ1(x,z)+λ2(y,z) (линейность по первому аргументу);
- ∀ x,y, ∈L
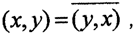 где черта означает комплексное сопряжение (эрмитова симметричность);
где черта означает комплексное сопряжение (эрмитова симметричность);
- ∀ x ∈L (x,x)≥0,причем (x,x)=0 ⇔ x=0.
Комментарий. (В определении мы абстрагируемся не только от природы изучаемых элементов и конкретного вида правил образования суммы элементов и произведения элемента на действительное число, но и от конкретного вида правила образования скалярного произведения двух элементов. Важно лишь, чтобы указанные правила удовлетворяли аксиомам. Бесконечномерные эвклидовы пространства часто называют предгильбертовыми. В действительном эвклидовом пространстве скалярное произведение (x,y) коммутативно, то есть (x,y)=(y,x), и линейно и по второму аргументу. Сложнее с комплексным эвклидовом пространством. Здесь 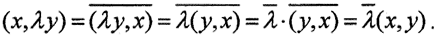 )
)
Определение 2.Эвклидовой нормой элемента x∈L называют 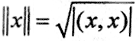 (как аналог длины вектора).
(как аналог длины вектора).
Пример. На множестве непрерывных функций, заданных на сегменте [a,b], определим скалярное произведение 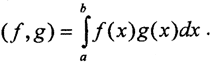 Покажем, что это - скалярное произведение.
Покажем, что это - скалярное произведение.
Из свойств интеграла очевидно выполнение первых двух аксиом. Покажем унитарность. По теореме о среднем 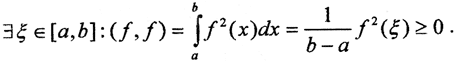 Покажем, что
Покажем, что 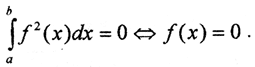 Если f(x)=0, то и
Если f(x)=0, то и 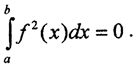 Покажем обратное. Пусть
Покажем обратное. Пусть 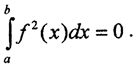 Покажем, что ∀x∈[a,b] f(x)=0.
Покажем, что ∀x∈[a,b] f(x)=0. 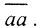 Пусть ∃x=x0:f(x)x=x0≠0. Тогда по теореме о сохранении знака непрерывной функции ∃ux0:f(x)≠0 ∀x∈ux0. Но тогда
Пусть ∃x=x0:f(x)x=x0≠0. Тогда по теореме о сохранении знака непрерывной функции ∃ux0:f(x)≠0 ∀x∈ux0. Но тогда 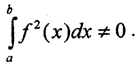 Эвклидова норма элементов в пространстве непрерывных функций
Эвклидова норма элементов в пространстве непрерывных функций 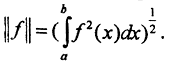
Комментарий. (Скалярное произведение на множестве непрерывных функций, заданных на сегменте [a,b], можно определить, например, как 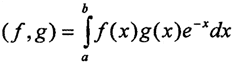 или как
или как 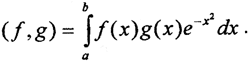 Так как скалярное произведение можно ввести различными способами, то и нормы тоже отличаются между собой (длину удава можно мерить и мартышками, и попугаями).)
Так как скалярное произведение можно ввести различными способами, то и нормы тоже отличаются между собой (длину удава можно мерить и мартышками, и попугаями).)
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'