5. Метод Лаврентьева

Уравнения вида Au=f, в которых правая часть f∈B(f_δ,δ)≠AM, изучались М. М. Лаврентьевым. Ему принадлежит идея замены исходного уравнения близким ему, в некотором смысле, уравнением, для которого задача нахождения решения устойчива к малым изменениям правой части и разрешима для любой правой части.

Пусть Au=f, где u - неизвестная функция, но предполагается её существование и единственность. Оператор A компактен, поэтому обратный оператор A^-1 неограничен. Априорно известно, что ||Au-f_δ||≤δ. Как обычно, считаем, что u∈D(A). На множестве D(A) мы можем выделить множество возможных решений M (тогда AM - образ множества M). Функция f может как принадлежать, так и не принадлежать множеству AM. То есть уже по постановке это существенно некорректная задача. М. М. Лаврентьев предложил решать вместо уравнения Au=f следующую задачу: (A+αE)u=f_δ, где f_δ∈F, а оператор A - компактный симметричный положительный оператор.

Теорема 1. Семейство операторов 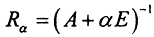является регуляризирующим для уравнения Au=f.

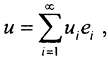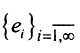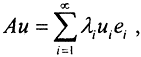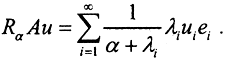□ Пусть где u_i=(u,e_i), последовательность - это полная ортогональная система собственных функций компактного оператора A, а соответствующую ей систему собственных значений оператора A обозначим через {λ_i}. Тогда по теореме Гильберта-Шмидта а Так как оператор A компактный симметричный положительный оператор, то его система собственных значений состоит из действительных положительных чисел с единственной предельной точкой - нулём. Расположив последовательность {λ_i} в порядке убывания, получим 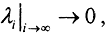то есть ∀α>0 - норма регуляризатора 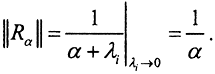Это значит, что оператор 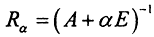непрерывен ∀α>0. □

Тогда приближённое решение имеет вид: u_δα=(A+αE)^-1f_δ.

Теорема 2 (М. М. Лаврентьев). Пусть A:H→H - компактный самосопряженный положительный оператор, α=α(δ)→0 при δ→0 и имеет менее высокий порядок малости. Тогда приближённое решение u_δα=(A+αE)^-1f_δ непрерывно зависит от правой части.

□ Нужно доказать, что 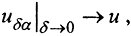то есть что ||u_δα-u||→0 при δ→0. Оценим норму разности ||u_δα-u||:

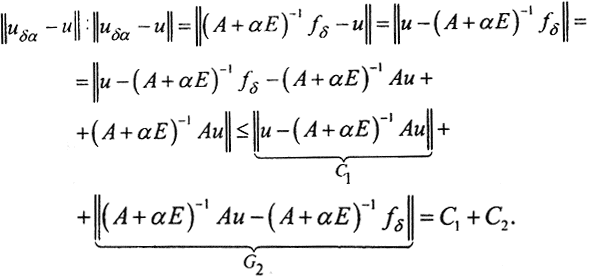
Отдельно оценим C₁ и C₂. Для этого сначала оценим ||(A+αE)^-1||.

1.Пусть в гильбертовом пространстве есть ПОНС 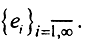Тогда:

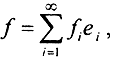
где f_i=(f,e_i), а Ae_i=λe_i. Разложим в ряд Фурье выражение: (A+αE)^-1f. Это разложение имеет вид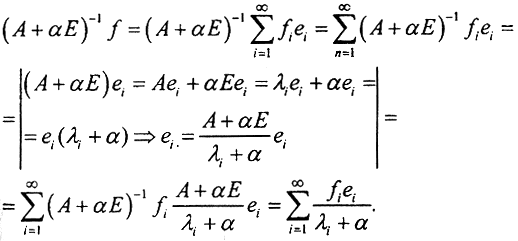

Тогда по определению нормы в гильбертовом пространстве

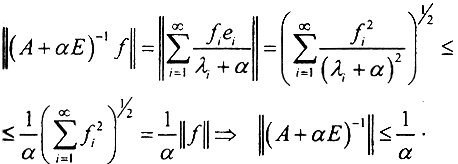
2. Оценим C₁:

C₁=||u-(A+αE)^-1Au||=||(A+αE)^-1Au-u||=||((A+αE)^-1A-E)u||.

Так как A-(A+αE)=-αE, то, умножив это выражение слева на (A+αE)^-1, сразу получим (A+αE)^-1A-E=(A+αE)^-1*(-αE). Тогда C₁ можно оценить таким образом:

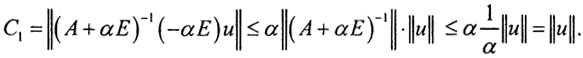
Разложение функции u в ряд Фурье имеет вид: 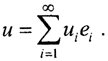Поэтому 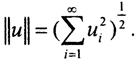С другой стороны, 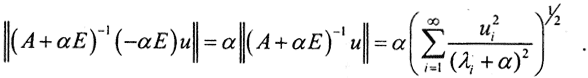Этот ряд сходится и C₁|_α→0→0, причём C₁≤α*C при α=const, где C - сумма ряда.

2. Оценим C₂:

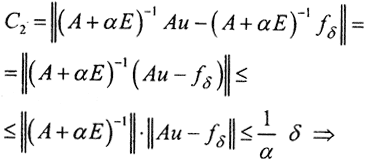
Так как α=α(δ)→0 при медленнее, чем δ, то С₂→0 при δ→0.

Таким образом, ||u_δα-u|||_δ→0→0. □

(Комментарий. С другой стороны, 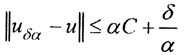при фиксированном значении α. То есть 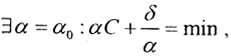при котором регуляризация будет наилучшей. Если значение очень велико или очень мало, то это не регуляризация. Выбор параметра регуляризации является сложной проблемой. Обычно на практике проводят расчеты с несколькими значениями параметра, составляющими геометрическую прогрессию (например, α={10^-1,10^-2,...,10^-6}). Из полученных результатов выбирают наилучший по какому-нибудь правдоподобному критерию. Например, таким критерием может быть требование, чтобы невязка, полученная при подстановке найденного u_α в исходное уравнение, была сравнима с погрешностью его правой части. Очевидно, воспроизводить правую часть с точностью, меньшей, чем эта погрешность, бессмысленно, равно как и в случае, когда погрешность много больше погрешности правой части.)

Если оператор A не обязательно положительный и самосопряженный, но ноль не принадлежит спектру оператора A, то есть решение уравнения Au=f единственно, применим к обеим частям этого уравнения оператор A^*. Тогда получится уравнение A^*Au=A^*f. Из единственности решения уравнения Au=f следует единственность решения уравнения A^*Au=A^*f. В самом деле, если A^*Au=0, то (A^*Au,u)=(Au,Au)=||u||²=0. Теперь R_α=(A^*A+αE)^-1A^*. Таким образом, в методе Лаврентьева операторному уравнению первого рода сопоставляется семейство операторных уравнений второго рода. Фактически, это частный случай практической реализации метода А.Н.Тихонова, состоящий в сведении задачи решения интегрального уравнения Фредгольма первого рода к решению интегрального уравнения Фредгольма второго рода 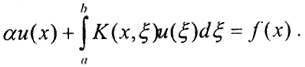Метод Лаврентьева является, наверное, самым простым и наглядным методом регуляризации.