6. Регуляризация интегрального уравнения Фредгольма I рода

Рассмотрим интегральное уравнение Фредгольма первого рода 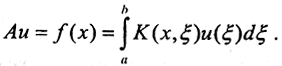Ранее доказано, что оператор является вполне непрерывным при действии L₂[a,b]→L₂[c,d] и при действии C[a,b]→L₂[c,d], а также то, что оператор, обратный к вполне непрерывному оператору, не может быть непрерывным. Поэтому задача решения интегрального уравнения Фредгольма первого рода некорректна. Это значит, что даже при очень малых ошибках в задании f(x) решение может либо отсутствовать, либо очень сильно отличаться от искомого точного решения. Некорректная задача называется регуляризируемой, если существует хоть один регуляризирующий алгоритм её решения. Все математические задачи, сводящиеся к решению операторного уравнения Au=f, могут быть классифицированы следующим образом:

• корректно поставленные;
• некорректные и регуляризируемые;
• некорректные и нерегуляризируемые.

Понятно, что корректно поставленные задачи регуляризируемы, поскольку в качестве регуляризирующего алгоритма можно выбрать обратный оператор.

Рассмотрим регуляризирующий алгоритм решения интегрального уравнения первого рода 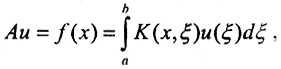предложенный А.Н.Тихоновым.

Полагаем, что его ядро K(x,ξ) непрерывно и таково, что в однородном случае уравнение имеет только тривиальное решение u(ξ)=0. Тогда при любой правой f(x)∈F решение либо единственно, либо не существует. Это значит, что интегральный оператор A взаимно-однозначно отображает пространства U→F. Пространство U обычно полагается пространством Соболева Wⁿ₂[a,b] с нормой 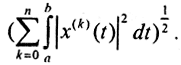Это гильбертово пространство, как и пространство F. Сходимость в пространстве Wⁿ₂[a,b] означает, что сама функция и все её производные, кроме n-й, сходятся равномерно, а n-я - среднеквадратично. То есть при n=0 регуляризация слабая, при n=1 сильная, а если n>1, то регуляризация гладкая порядка (n-1). При больших n решение сильно сглажено. Обычно полагают n=1. В вариационной форме задачу можно представить как 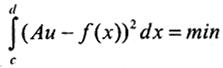и построить сглаживающий функционал 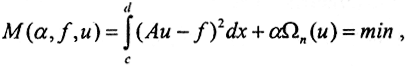где функционал Ω_n(u) называется стабилизатором n-го порядка. Его обычно строят так: 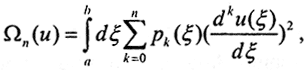где p_k(ξ) - непрерывные и неотрицательные весовые функции, которые равны единице, если нет причин полагать иначе. Положим для простоты, что ∀ p_k(ξ)=1, n=1. Тогда 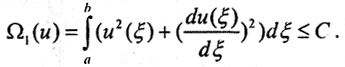Далее будем полагать, что u ∈C¹[a,b]. Ясно, что из сходимости в C¹[a,b] не следует сходимость в W₂ⁿ[a,b], но можно показать, что теорема Тихонова о регуляризации имеет место и в общем случае.

Лемма о компактности. Семейство непрерывно дифференцируемых на сегменте [a,b] функций, таких что ||u||²+||u'||²≤C², C>0, компактно.

□ Рассмотрим семейство непрерывно дифференцируемых на [a,b] таких функций, что ||u||²+||u'||²≤C², C>0. Ясно, что ||u||≤C, ||u'||≤C.

Покажем равностепенную непрерывность. Рассмотрим ∀ξ₁,ξ₂∈[a,b] 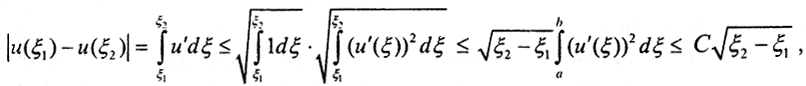а это и означает равностепенную непрерывность. Покажем равномерную ограниченность. Так как 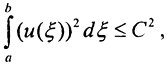то, применяя теорему о среднем, получим 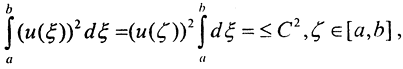, откуда сразу 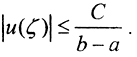Возьмём произвольную точку ξ∈[a,b]. Тогда u(ξ) можно представить так: 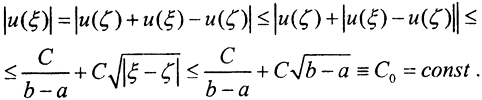Поскольку C₀ - константа, наше множество функций равномерно ограничено. Тогда по критерию Арцела это множество функций компактно в пространстве C[a,b].

Запишем с учётом наших упрощений запишем сглаживающий функционал M(α,f,u) Тихонова в таком виде: M(α,f,u)=||Au-f_δ||²+α(||u||²+||u'||²), где f_δ - непрерывная на [c,d] функция, такая, что ||f-f_δ||≤δ, δ∈(0,δ₀], δ₀>0, а Au=f. Здесь u - точное решение уравнения Фредгольма первого рода с непрерывным по совокупности аргументов и замкнутым ядром K(x,ξ), x∈[c,d], ξ∈[a,b] при точно известной правой части f, где f - непрерывно дифференцируемая на [a,b] функция. Обозначим функцию, на которой достигается минимум функционала Тихонова M=M(α,f,u), через u_α(δ)=argminM(α,f,u). Тогда M(α,f,u_α(δ)=M_δ. Ясно, что M_δ≤M. Напомним, что оператор A действует из C[a,b] в L₂[a,b] при условии, что точное решение u∈C¹[a,b].

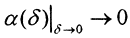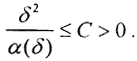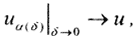Теорема Тихонова о регуляризации. Пусть параметр регуляризации α такой, что и, кроме того, Тогда где u - точное решение, а u_α(δ) - регуляризированное решение.

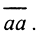□ Пусть регуляризированное решение u_α(δ)|_{δ →0} не стремится к точному решению u(ξ). Тогда ∃ε>0 и 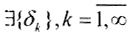такие, что ||u_α(δ)-u||≥ε>0. Так как M_δ≤M=||Au-f_δ||²+α(||u||²+||u'||²)≤δ²+α(||u||²+||u'||²), то ||Au_α(δ)-f_δ||²+α(||u_α(δ)||²+||u'_α(δ)||²)≤δ²+α(||u||²+||u'||²). Оба члена в левой части неотрицательны. Поэтому 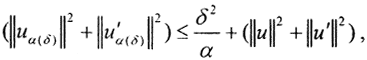, и если α=α(δ), то 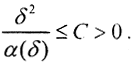Тогда ||u_α(δ)||²+||u'_α(δ)||²≤C₀=const. Тогда из доказанной леммы следует, что последовательность 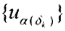компактна в пространстве C[a,b], то есть из неё можно выделить подпоследовательность, которая будет равномерно сходиться к некоторой непрерывной на [a,b] функции u₀. Не ограничивая общности, будем полагать, что 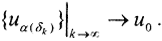Тогда

Но из неравенства ||Au_α(δk)-f_δ||+α(||u_α(δ)||²+||u'_α(δ)||²)≤δ²+α(||u||²+||u'||²) следует, что ||Au_α(δk)-f_δ||²≤δ²_k+α(||u||²+||u'||²). Тогда при переходе к пределу при k→∞ сразу получим, что ||Au₀-f||²=||Au₀-Au||²=0, то есть Au₀-Au=0, а это значит, что u₀=u. Другими словами, ||u_α(δk)-u|||_k→∞→0, что противоречит исходному предположению. □

Пример. Рассмотрим интегральное уравнение 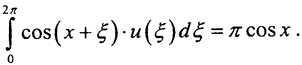Его точное решение имеет вид: u(x)=cosx.

Будем искать численное решение уравнения 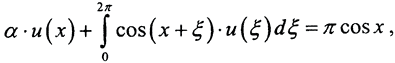которое при уменьшении параметра α стремится к решению исходного уравнения.

α=10^-15

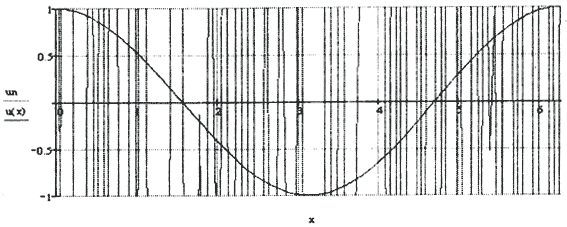
α=10^-14

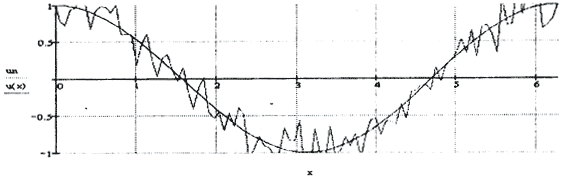
α=10^-4

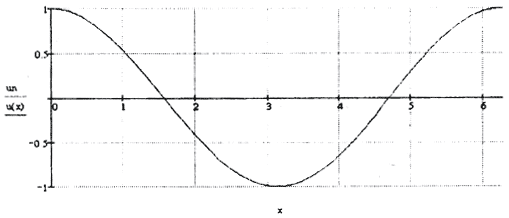
α=1

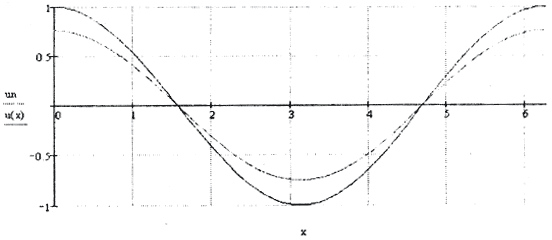
Существуют и другие методы регуляризации.

Пример. Рассмотрим задачу теплопроводности с обратным временем: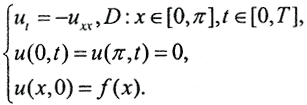

Решение этой задачи: 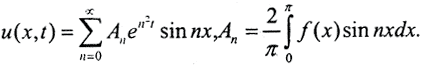Рассмотрим семейство линейных операторов 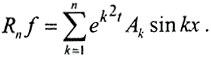При n→∞ регуляризированное решение будет сходиться к точному, если f(x) и u(x,t) рассматривать в пространстве L₂. В самом деле, операторы определения коэффициентов Фурье f_k и суммирования непрерывны, отсюда и непрерывность операторов R_n, а сходимость последовательности R_nf следует из сходимости ряда Фурье в L₂.

Другой способ регуляризации - замена исходного некорректного уравнения пусть неустойчивым, но корректным уравнением путём добавления слагаемых, содержащих частные производные, в исходное уравнение, то есть изменения самого уравнения.

Пример. □ Для уравнения теплопроводности с обратным временем рассматривается уравнение u_t=-u_xx-αu_x⁴ с начальными данными u(x,0)=f(x), f(0)=f(π)=0, u(0,t)=0, t∈[0,T]. Дополнительно потребуем, чтобы u_xx(0,t)=u_xx(π,t)=0. В результате получим решение прямой задачи: 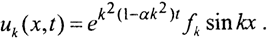Видно, что при α→0 мы получаем решение исходного некорректного уравнения, то есть полученное решение регуляризирует исходную задачу. Так как 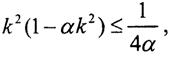то норма решения прямой задачи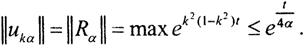

Nunk dimittis, примерно с этого места и начинается то, что называется теорией обратных некорректных задач и практикой их вычислительного применения. Однако это требует значительно более глубокого знания и функционального анализа, и теории интегральных уравнений, и вариационного исчисления.