3. Принцип отбора решений

Этот принцип называется вариационным или стандартной схемой отбора решений Тихонова. Полагаем, что точное решение u∈M⊂D(A).

1) Построим на множестве M функционал Ω(u) так, чтобы он был, по крайней мере, неотрицательным (лучше, когда он выпуклый). В предыдущей главе функционал Ω(u)=||u||² является, очевидно, выпуклым. Функционал Ω_n(u) называется стабилизатором;

2) на некотором компактном множестве M_k⊂M решаем уравнение Эйлера и показываем, что минимум Ω(u) достигается на некоторых элементах u_δ∈M_k.

3) далее строим функционал M(u,δ,α) α=α(δ) α(δ)|_δ→∞→0. Функционал M(u,δ,α) называется сглаживающим.

4) решается задача нахождения минимума M(u,δ,α), который достигается на элементах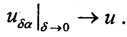

Получение при каждом α соответствующего u_δα равносильно применению к правой части уравнения оператора R_α, который называется регуляризирующим оператором. Тогда приближенное решение находится так: R_αf_δ=u_δα. Таким образом, задача нахождения приближенного решения уравнения Au=f, устойчивого к малым изменениям правой части, сводится во-первых, к нахождению регуляризирующих операторов, а во-вторых, к определению параметра регуляризации α по дополнительной информации о задаче, например по величине погрешности, с которой задаётся правая часть f_δ. Этот метод построения приближённых решений называется методом регуляризации.