2.1. Скелетное разложение прямоугольной матрицы

Рассмотрим матричное уравнение AXA=A. Если A - квадратная неособенная матрица, то это уравнение имеет единственное решение A^-1AXA=A^-1A⇔XA=E, X=A^-1 Если же A - произвольная прямоугольная m*n-матрица, то искомое решение Х имеет размеры m*n и уравнение имеет бесконечное множество решений. Рассмотрим произвольную m*n-матрицу A и СЛАУ AX=Y. Покажем, что в случае недоопределённой СЛАУ существует и единственно решение с минимальной нормой x=A⁺y, где A⁺ - псевдообратная матрица.

B дальнейшем мы будем пользоваться представлением произвольной прямоугольной m*n-матрицы A=BC. Матрица B имеет размер m*r, а матрица C имеет размер r*n, где r - ранг матрицы A. В качестве матрицы B можно взять любые r линейно независимых столбцов матрицы или любые их линейные комбинации. Матрица C подбирается таким образом, чтобы A=BC. Это выбор не однозначен. Поскольку матрицы B и C имеют максимально возможный ранг, то квадратные матрицы B^*B и C^*C невырождены.

Уравнение B^*Bx=0 умножим слева на x^*. Тогда (Bx)^*(Bx)=0. Это скалярный квадрат, то есть Bx=0 при x=0.

Определение. Представление произвольной прямоугольной m*n-матрицы A=BC и называется скелетным разложением.

Определение. Матрица A⁺_n*m называется псевдообратной для матрицы A_n*m, если выполняются равенства AA⁺A=A, A⁺=UA^* и A⁺=A^*V, где U и V - некоторые матрицы.

Первая теорема Мура-Пенроуза. Псевдообратная матрица существует и единственна.

□ Единственность. Пусть существуют A₁ и A₂ - две различные псевдообратные матрицы, а U и V - какие-то матрицы. Тогда AA⁺₁A=AA₂⁺A=A, A⁺₁=U₁A^*=A^*V₁, A⁺₂=U₂A^*=A^*V₂, D=A⁺₁+A⁺₂, U=U₁-U₂, V=V₁-V₂. Тогда A(A⁺₁-A⁺₂)A=AA⁺₁A-AA⁺₂A=0. То есть ADA=0. Построим скалярный квадрат DA: D^*=(UA^*)^*=AU^*=(A^*V)^*=V^*A .Отсюда (DA)*DA = A*D*DA = A*V*ADA = 0 и, следовательно, DA=0. Но тогда DD*= DAU*=0, то есть D=0. A⁺₁-A⁺₂=0.

Существование. Так как по определению должны иметь место равенства BB⁺B=B, B⁺=UB^*=B^*V, где U - некоторая матрица, то BUB^*B=B. Умножая слева на В* и замечая, что В*В - неособенная квадратная матрица, найдем U=(B^*B)^-1, то есть B⁺=(B^*B)^-1B^*. Совершенно аналогично найдем: CC⁺C=C, C⁺=C⁺V, C⁺=C^*(CC^*)^-1. Покажем, что матрица A⁺=C⁺B⁺=C^*(CC^*)^-1(B^*B)^-1B^* есть псевдообратная матрица для матрицы A.

1. AA⁺A=BCC^*(CC^*)^-1(B^*B)^-1B^*BC=B((CC^*)(CC^*)^-1)((B^*B)^-1(B^*B))C=BC=A.

2.Обозначим K=(CC^*)^-1(B^*B)^-1. Тогда A⁺=C^*KB^*=(C^*K(CC^*)^-1C)C^*B^*=UA^* и, наконец, A⁺=C^*KB^*=C^*B^*(B(B^*B)^-1KB^*)=A^*V. □

Вторая теорема Мура-Пенроуза. Псевдообратная матрица минимизирует не только невязку, но и норму, то есть x₀=A⁺y.

□ Рассмотрим невязку y-Ax=u+v, u=y-Ax₀=y-AA⁺y, v=A(x₀-x). Тогда |y-Ax|²=(y-Ax)^*(y-Ax)=(u+v)^*(u+v)=u^*u+v^*u+u^*v+v^*v. Но v^*u=(x₀-x)^*A^*(y-AA⁺y)=(x₀-x)^*(A^*-A^*AA⁺)y, A^*AA⁺=C^*B^*BCC^*(CC^*)^-1(B^*B)^-1B^*=C^*B^*=A^*, то есть v^*u=0. Но тогда u^*v=(v^*u)^*=0, а |y-Ax|²=|u|²+|v|²=|y-Ax₀|²+|A(x₀-x)|². Это значит, что |y-Ax|≥|y-Ax₀|. Пусть теперь |y-Ax|=|y-Ax₀|. Обозначив, z=x-x₀, получим Az=0. Тогда |x|²=(x₀+z)^*(x₀+z)=|x₀|²+|z|²+x₀^*z+z^*x₀, а A⁺=A^*V. Отсюда сразу получим x₀^*z=(A⁺y)^*z=(A^*Vy)^*z=y^*V^*Az=0. Но тогда z^*x₀=(x₀^*z)^*=0 и |x|²=|x₀|²+|z|², то есть |x|²≥|x₀|². □

Пример. Найти псевдообратную матрицу A⁺ для матрицы 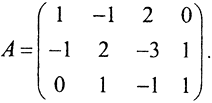Так как rangA=2, положим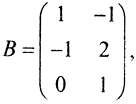 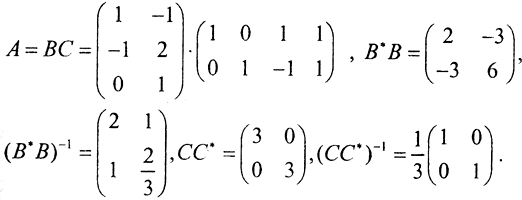Тогда

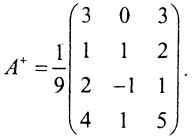
Пример. Решить систему 2x-3y=4. Она имеет вид Ax^_=f^_. A=(2,-3), BC=A, rangA=1, 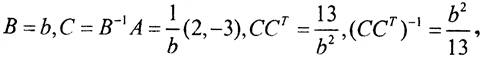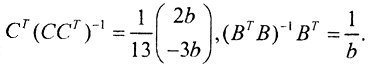A⁺=C^T(CC^T)^-1(B^TB)^-1B^T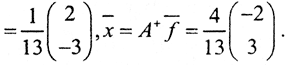

Пример. Рассмотрим уравнение αx=β. α ≠0⇒x=^β/_α, α=0⇒0x=β⇒β=0. Результат тот же, как если бы x=^β/_α доопределили в нуле. В общем случае то же самое: псевдорешение не является непрерывной функцией от элементов матрицы и свободных членов. Рассмотрим матрицу размера m*n.

1. Если m=n, detA≠0. Решение теоретически всегда существует. Обратная матрица существует. Точность решения сильно зависит от числа обусловленности: точность вычислений можно увеличить, если condA<1000; если condA>1000 то нельзя гарантировать никакой точности.

2. Если m≠n и rangA=min{m,n}, то говорят, что матрица A имеет полный ранг. В этом случае при любой матрице A нормальное псевдорешение непрерывно зависит от правой части, так как является проекцией на образ A. Проекция единственная, оператор проецирования - линеен, обратный к нему - также линеен, пространство конечномерное. Таким образом, из линейности оператора следует его непрерывность, а из непрерывности следует, что малые изменения оператора соответствуют малым изменениям решения. Позже мы покажем, что для действительной матрицы A в этом случае A⁺=(A^TA)^-1A^T.

3. Если rangA<min{m,n}, то матрица А имеет неполный ранг, её нормальное псевдорешение всегда разрывное. В этом случае без привлечения дополнительной информации улучшить точность решения невозможно. Простейший способ введения дополнительной информации и параметризации задачи (для решения однотипных корректных задач) даёт так называемая стандартная схема Тихонова, которая будет разобрана в следующей главе.