IX. Стандартная схема регуляризации СЛАУ

Ну, это стандартная процедура, 
сказала Сова. 
Что такое ондатравая цедура? 
спросил Вини Пух. 
Не забывай, у меня в голове опилки 
и длинные слова меня смущают.

А.Милн. "Вини Пух и всё, всё, всё."

Рассмотрим СЛАУ Ax=b. Ясно, что A,b не точные, так как они получены в результате измерения. Поэтому на самом деле система имеет вид: A_μx=b_δ, где ||A-A_μ||≤μ, ||b-b_δ||≤δ. Рассмотрим функционал M(A_μ,b_δ,x,α)=||A_μ-b_δ||²+α||x||², где α>0 - достаточно малый стабилизирующий параметр - параметр регуляризации. Уравнения, минимизирующие любой функционал, называются уравнениями Эйлера. А решения этих уравнений называются экстремалями. Функционал ||x||² называется стабилизатором. Функционал M(A_μ,b_δ,x,α)- сглаживающим.

Теорема 1. Экстремали функционала М лежат на решении уравнения: (A^*_μA_μ+αE)x=A^*_μb_δ, α,μ,δ>0.

□ Найдем первый дифференциал:

dM=d[(A_μx-b_δ,A_μx-b_δ)+α(x,x)]=2[(A_μdx,A_μx-b_δ)+α(x,x)]=2[(dx,A_μ^*A_μx-A_μ^*b_δ)+(dx,αx)]=2[(dx,(A_μ^*A_μ+αE)x-A_μ^*b_δ]=0 ⇒(A_μ^*A_μ+αE)x=A_μ^*b_δ.

Найдем второй дифференциал:

d²M=d[(dx,(A_μ^*A_μx-A_μ^*b_δ)+α(dx,dx)]=d(dx,(A_μ^*A_μ+αE)x-A_μ^*b_δ)=(dx,A_μ^*A_μdx+αdx)=(A_μdx,A_μdx)+α(dx,dx)=||A_μdx||²+α||dx||²&362;0.

Так как второй дифференциал больше нуля, то это минимум. □

Определение. Уравнение (A_μ^*A_μ+αE)x=A_μ^*b_δ называется регуляризирующим уравнением Тихонова, а его решение называется регуляризованным.

Теорема 2. Для любого оператора А оператор (A^*A+αE) будет положительным, самосопряженным и обратимым.

□ 1. Докажем положительность по определению:

((A^*A+αE)x,x)=(A^*Ax,x)+α(x,x)+(Ax,Ax)+α(x,x)=||Ax||²+α||x||².

2. Обратимость докажем от противного: Обратимость эквивалентна существованию обратного оператора (A^*A+αE)^-1, а оператор обратим, если его ядро состоит из единственного нулевого элемента, то есть каждому элементу из образа Im(A^*A+αE) сопоставляется единственный элемент из D(A^*A+αE), а ноль переходит в ноль. Пусть Ker(A^*A+αE)≠ {0} ⇒∃ξ≠0:ξ∈Ker∈ ((A^*A+αE)ξ,ξ)>0, так как оператор (A^*A+αE) положителен) ⇒ (0ξ,ξ)>0 - неверно, так как (0ξ,ξ)=0.

3. Самосопряженность очевидна. □

Пример. Решить СЛАУ 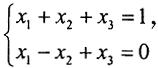методом регуляризации, найдя предварительно нормальное решение. Сравнить полученные решения. Установить зависимость ||x_α-x_n|| от α.

□

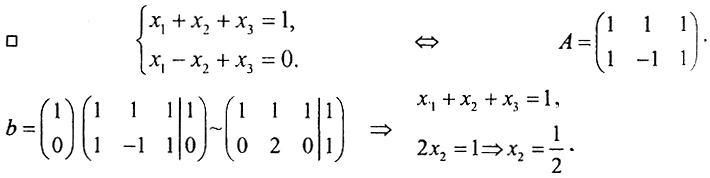
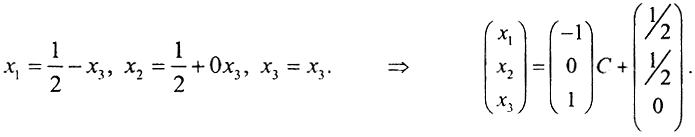
Минимизируем норму: 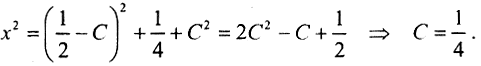. Нормальное решение имеет вид 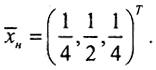Теперь получим решение методом регуляризации: 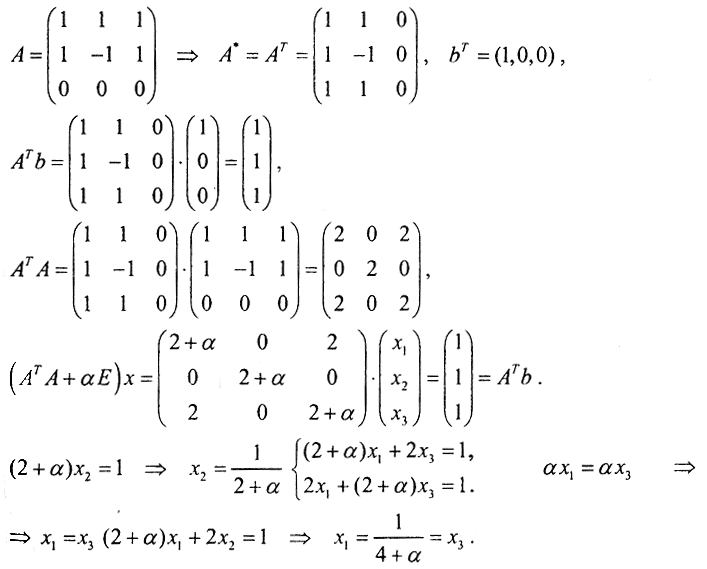Таким образом, регуляризированное решение имеет вид 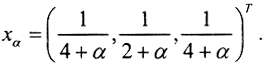Видно, что, если α устремить к 0, регуляризованное решение совпадет с нормальным, а □

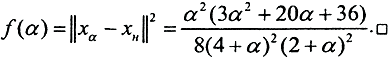Пример. Решить систему 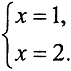Установить зависимость ||x_α-x_н|| от α.

Так как 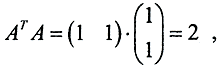то 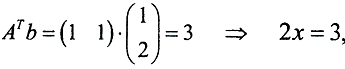то есть x=1,5. Получим регуляризованное решение: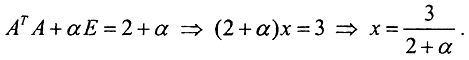

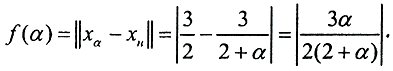
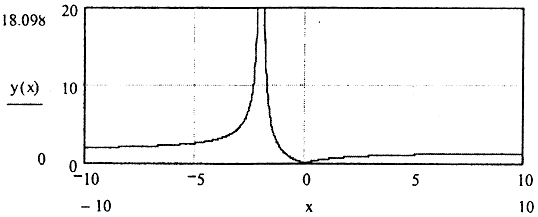
Видно, что если α устремить к 0, регуляризованное решение совпадет с нормальным. График f(α) имеет вид (напомним, что параметр регуляризации α>0):

Теорема 3. Пусть система Ax=b совместна. Тогда регуляризованное решение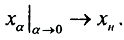

□ Нормальное псевдорешение совпадает с решением системы: Ax=b^_, b^_=Пр_ImAb*Ax-b^_∈ImA, ImA⊥KerA, (b^_-b)∈KerA.

||Ax-b-b^_+b^_||²=||(Ax-b^_)+(b^_-b)||²=||Ax-b^_||²+||b-b^_||²

M(A,b,x,α)=||Ax-b||²+α||x||²=M(A,b,x,α)=M(A,b^_,x,α)+||b-b^_||²⇒M(A,b^_,x,α)≤M(A,b,x,α) ⇒α||x_α||²<M(A,b,x_α,α). Очевидно, что x_α минимизирует оба функционала, так как ||b-b^_||²=const. Тогда M(A,b,x_n,α)=||Ax-b||+α||x||²M(A,b,x,α)=||b-b^_||⇒α||x_α||²<M(A,b,x_α,α)<M(A,b,x_н,α)=α||x_н||², то есть ||x_α||≤||x_н||. Покажем, что 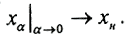В конечномерном евклидовом пространстве решение х_α находится в шаре радиуса х_н. Рассмотрим последовательность 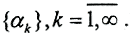Так как наше пространство - компакт, то из неё можно выделить сходящуюся подпоследовательность 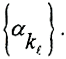Ей соответствует последовательность векторов 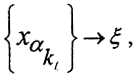где ξ - некоторый вектор. Эта последовательность минимизирующая, так как ||ξ||≤||x_н||. С другой стороны, ||ξ||≥||x_н||, так как x_н - проекция. Таким образом, имеем ξ=x_н в силу единственности x_н. □

Следствие.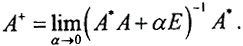

□ Если b∈ImA, то решение Ax=b:x=A⁺b. С другой стороны x_α=(A^*A+αE)^-1A^*b. Так как 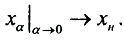то, сравнивая, получим искомое. □