
3. Несовместные системы. Метод матрицы Грама
3.1. Проецирование на заданные линейные оболочки
Решение многих задач, имеющих практическое значение, не существует по определению. Это тот случай, когда в решении задачи есть некий компромисс между противоречивыми требо-ваниями. Если так или иначе задана или легко определима какая-либо ортонормированная система, то получаем задачу минимизации невязки. В случае СЛАУ часто невыгодно искать ОНС. Проще осуществлять проецирование на заданные линейные оболочки. Пусть h=x-x_ - невязка, линейная оболочка L(a1,...,an), искомый вектор 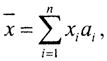 где {x1,...,xn} - неизвестные. Так как h⊥L, то есть h⊥∀ai,
где {x1,...,xn} - неизвестные. Так как h⊥L, то есть h⊥∀ai, 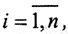 то запишем это условие ортогональности:
то запишем это условие ортогональности:
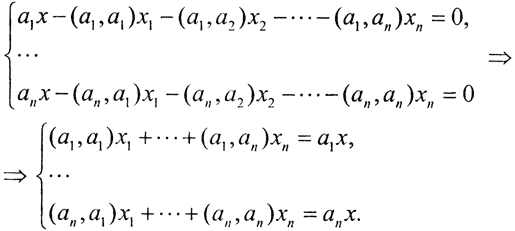
Получим симметрическую, всегда совместную СЛАУ. Главная матрица системы - матрица Грама 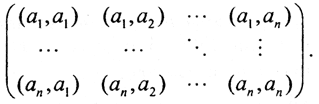 Таким способом мы найдем решение, принадлежащее линейной оболочке L, с минимальной невязкой.
Таким способом мы найдем решение, принадлежащее линейной оболочке L, с минимальной невязкой.
Пример. Найти проекцию вектора х={2,-5,3,4} на линейную оболочку L(a1,a2,a3), где a1={1,3,3,5}, a2={1,3,-5,-3}, a3={1,-5,3,-3}.
(a1a2)=1+9+9+25=44,
(a2a2)=1+9+25+9=44,
(a3a3)=1+25+9+9=44,
(a1a2)=(a2a1)=1+9-15-15=-20,
(a1a3)=(a3a1)=1-15+9-15=-20,
(a2a3)=(a3a2)=1-15-15+9=-20,
(a1x)=2-15+9+20=16,
(a2x)=2-15-15-15=-40,
(a3x)=2+25+9-12=24,
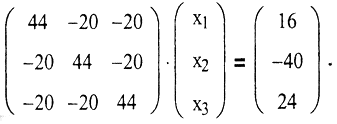
Решение с минимальной невязкой, принадлежащее линейной оболочке L(a1,a2,a3), то есть псевдорешение, имеет вид 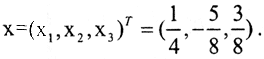 Следовательно,
Следовательно, 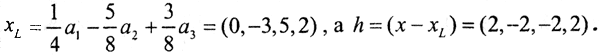
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'