
4. Теоретические оценки устойчивости
4.1. Устойчивость обратной задачи теплопроводности
Обратная задача теплопроводности имеет вид:
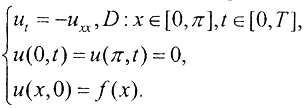
Проведем оценку устойчивости обратной задачи теплопроводности для множеств решений, ограниченных в гильбертовом пространстве L2, так как в этих случаях и вид функций, и способ их получения наиболее просты.
□ Пусть u(x,t) - решение поставленной краевой задачи, а класс корректности 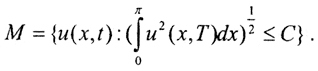 Определим
Определим 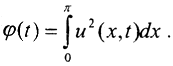 Тогда
Тогда 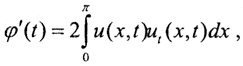 а
а 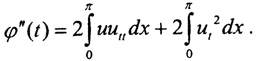 Преобразуем первое слагаемое, учитывая, что utt=(ut)t=-(-uxx)xx=uxxxx. Тогда
Преобразуем первое слагаемое, учитывая, что utt=(ut)t=-(-uxx)xx=uxxxx. Тогда 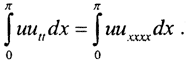 Интегрируем по частям, полагая g=u, dg=uxdx, dv=uxxxxdx=d(uxxx), v=uxxx. Тогда
Интегрируем по частям, полагая g=u, dg=uxdx, dv=uxxxxdx=d(uxxx), v=uxxx. Тогда 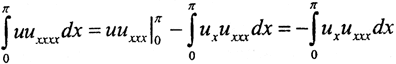 (граничные условия обращают в ноль первое слагаемое). Этот интеграл опять берём по частям: g=ux, dg=uxxdx, dv=uxxxdx=d(uxx), v=uxx.
(граничные условия обращают в ноль первое слагаемое). Этот интеграл опять берём по частям: g=ux, dg=uxxdx, dv=uxxxdx=d(uxx), v=uxx.
Тогда 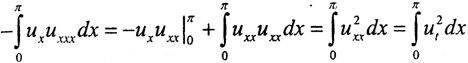 и сразу
и сразу 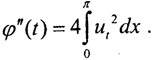 Рассмотрим функцию ψ(t)=lnφ(t). Так как
Рассмотрим функцию ψ(t)=lnφ(t). Так как 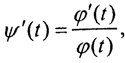
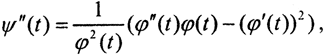 то
то 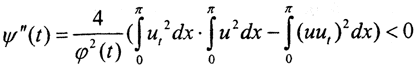 (из неравенства Буняковского Коши). Таким образом, функция ψ(t) выпукла вниз, лежит не ниже своей касательной, то есть на отрезке t∈[0,T] не превосходит линейную функцию, принимающей на концах отрезка те же значения, что и ψ(t). Уравнение прямой, проходящей через точки A(0,ψ(0)), B(T,ψ(T)), имеет вид
(из неравенства Буняковского Коши). Таким образом, функция ψ(t) выпукла вниз, лежит не ниже своей касательной, то есть на отрезке t∈[0,T] не превосходит линейную функцию, принимающей на концах отрезка те же значения, что и ψ(t). Уравнение прямой, проходящей через точки A(0,ψ(0)), B(T,ψ(T)), имеет вид 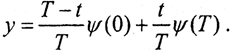 Таким образом,
Таким образом, 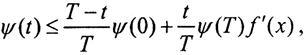 то есть
то есть 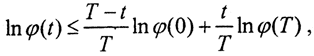 откуда, потенцируя, получаем
откуда, потенцируя, получаем 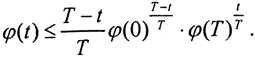 Пусть u1(x,t), u2(x,t) - функции из класса корректности, удовлетворяющие задаче, причём
Пусть u1(x,t), u2(x,t) - функции из класса корректности, удовлетворяющие задаче, причём 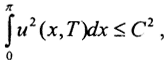 а
а 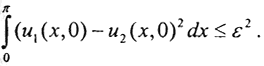 Тогда
Тогда 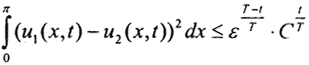 и искомая оценка имеет вид
и искомая оценка имеет вид 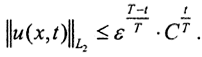 □
□
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'