4.2. Оценка устойчивости задачи дифференцирования

Задача дифференцирования относится к типу задач, которые могут быть сведены к интегральному уравнению Фредгольма I рода. Она ставится так.

Пусть на [a,b] задана функция f(x). Оценить её производную f'(x) и показать непрерывность оператора дифференцирования на множестве корректности M.

□ Пусть f'(x)=u(x), f(x)∈F, u(x)∈U, AF=U, 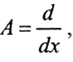F=U=C[a,b], f(x)∈M={f(x):f"(x)∈C[a,b], ||f"(x)||≤m}, M - множество корректности, т.е. множество дважды непрерывно дифференцируемых функций с ограниченной второй производной. Рассмотрим две функции: f₁(x), f₂(x):f₁(x)-f₂(x)=φ(x), причём |φ(x)|<ε. Тогда |φ"(x)|<2m. Так как φ'(x) непрерывна ∀x∈[a,b], то ∃x₀∈[a,b]:φ'(x₀)=max|φ'(x)|. Будем полагать, что φ'(x)|_x=x0>0, x₀<x. При других вариантах доказательство аналогично. Тогда φ'(x) выпукла вверх и x<x₀ при φ"(x)<0. 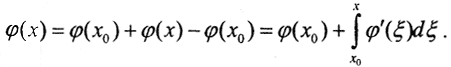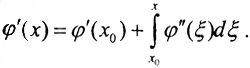Представим Тогда Так как φ"(x)∈[-2m,2m], то φ"(x)≥-2m.Таким образом, φ'(x)≥φ'(x₀)-2m(x-x₀). Подставим это в выражение для φ(x), и, заменяя φ'(x) на меньшее выражение, получим 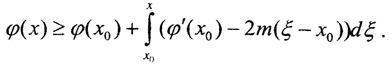Проинтегрировав, получим φ(x)≥φ(x₀)+φ'(x₀)(x-x₀)-m(x-x₀)², то есть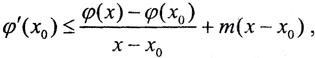 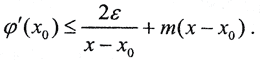Положив 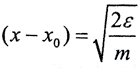(ε достаточно мало, а 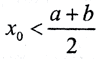), сразу получим 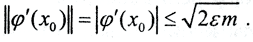Отсюда и следует непрерывность оператора дифференцирования на множестве корректности M. □

Из за погрешности исходных данных элемент y может не принадлежать множеству AM. В этих условиях уравнение не имеет классического решения и не ясно, что надо понимать под приближенным решением уравнения Ax=y и как его находить. Это и обсуждается в следующей главе.