3. Метод библиотеки

Если мы решаем задачу в классе корректности по Тихонову, то наиболее общим, но громоздким является метод библиотеки, или метод подбора. Идея этого метода состоит в том, что для элементов некоторого заранее заданного подкласса возможных решений M⊂X вычисляется оператор Ax, т. е. решается прямая задача. В качестве приближенного решения берется такой элемент x_0∈M, на котором невязка ρ_y(Ax,y) достигает минимума, то есть x₀=arginf_x∈Mρ_y(Ax,y). Пусть правая часть уравнения известна точно, то есть y=y_T, и требуется найти его решение x_T. Если искомое точное решение x_T принадлежит множеству M, то 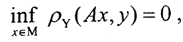и достигается эта нижняя граница на точном решении x_T. Если уравнение имеет единственное решение, то элемент x₀, минимизирующий ρ_y(Ax,y), определен однозначно.

Практически минимизация невязки ρ_y(Ax,y) производится приближенно. Поэтому возникает вопрос об эффективности и обоснованности метода подбора. Пусть {x_n} - последовательность элементов, для которой ρ_y(Ax,y)|_n→∞→0. При каких условиях можно утверждать, что при этом и ρ_X(x_n,y_T)|_n→∞→0, то есть что последовательность {x_n} сходится к x_T?

Ответ основывается на следующих теоремах.

Теорема 1 (критерий Фреше - Хаусдорфа). Пусть X - банахово пространство, а M⊂X. Множество M - компактно, если и только если M вполне ограничено в X.

(Комментарий. Множество M⊂X называется вполне ограниченным, если ∀ε>0 в множестве X найдётся для M конечная ε-сеть ("конечный скелет"), то есть конечное множество E⊂X:∀x⊂M∃x_ε∈E:ρ(x,x_ε)<ε.)

□ Необходимость. Пусть множество M - компакт. Покажем полную ограниченность множества M. Зафиксируем ε>0, выберем произвольную точку x₁ ∈ M и построим открытый шар B₁(x₁,ε). Может случиться так, что ∀x⊂M⊂B₁(x₁,ε). Это означает, что точка x₁ образует конечную ε-сеть для множества M, состоящую из одного элемента, то есть теорема доказана. Если это не так, то ∃ x₂∈M, x₂∉(B₁(x₁,ε):ρ(x₁,x₂)>ε. Если теперь ∀x⊂M⊂B₁(x₁,ε)?B₂(x₂,ε)), то точки x₁ и x₂ образуют конечную ε-сеть для M, состоящую из двух элементов, то есть теорема доказана. Если это не так, то ∃ x₃∉(B₁(x₁,ε?B₂(x₂,ε)):ρ(x₂,x₃)>ε. Если процесс закончится, то конечная ε-сеть построена, а если нет, то 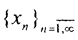не фундаментальна, так как ρ(x_i,x_j)≥ε, то есть не сходится, что противоречит определению компакта.

Достаточность. Пусть M⊂X - вполне ограниченное множество в полном метрическом пространстве (X,ρ). Покажем, что M - компакт. Так как M полностью ограниченно, то для любого ε>0 в метрическом пространстве (X,ρ) существует конечная ε-сеть для множества M, то есть существует конечное покрытие элементов из M открытыми шарами радиуса ε. Пусть {x_n} - произвольная последовательность элементов из M. Тогда, в соответствии с принципом Вейерштрасса, существует хоть один шар, содержащий бесконечное число членов последовательности {x_n}, то есть содержащий подпоследовательность {x_n}, расстояние между элементами которой меньше ε. Пусть 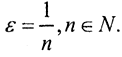Выделим из последовательности {x_n} подпоследовательность 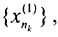расстояние между элементами которой меньше ε. Из этой подпоследовательности выделим подпоследовательность 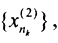расстояние между элементами которой меньше 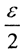и т.д. Таким образом, мы получили последовательность подпоследовательностей 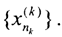Тогда члены "диагональной" последовательности 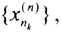начиная с некоторого номера k принадлежат k-й подпоследовательности, то есть 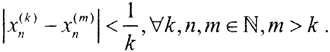То есть последовательность {x_n} фундаментальна, а так как банахово пространство (X,ρ) полное, то 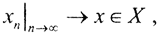то есть M⊂X - компакт или предкомпакт. □

Теорема 2 (А.Н.Тихонов). Пусть в операторном уравнении Ax=y оператор A - взаимно однозначный НЛО: AM=N, где M компактно, M⊂X, N⊂Y.Тогда:

3) решение уравнения равномерно непрерывно зависит от его правой части.

□ 1. Покажем, что образ компактного множества M тоже компактен. Непрерывность оператора A на языке Гейне означает, что для любой последовательности {x_n} → x₀ соответствующая последовательность {Ax_n}→Ax₀=y₀. Так как множество M⊂X компактно, то есть ∀{x_n}∈M можно выделить {x_nk}→ x₀ ∈M(M^_). Тогда, в силу непрерывности оператора A, соответствующая последовательность {Ax_nk}={y_nk}→ y₀ ∈AM или замыканию AM^_), а это и означает, что множество AM=N компактно.

2. Покажем, что оператор A^-1 существует и непрерывен. 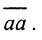Пусть A^-1 не является непрерывным на M. Так как оператор A-НЛО, а M⊂X компактно, то из любой последовательности {x_n} можно выделить сходящуюся подпоследовательность: {x_nk}→ x₀. Тогда соответствующая последовательность {Ax_nk}={y_nk}→ y₀ ∈AM. Так как A^-1 не является непрерывным на AM, то из последовательности 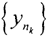можно выделить подпоследовательность 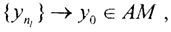но соответствующая ей последовательность 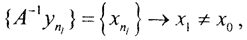то есть не будет сходиться к x₀. Но оператор A-НЛО, т.е. 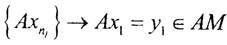и у последовательности {y_n} есть два предела. Получили противоречие. Поэтому оператор A^-1 - непрерывный взаимно-однозначный оператор.

3. Покажем, что решение уравнения равномерно непрерывно зависит от его правой части, то есть ∀ x₁,x₂ ∈M ∀ε>0 ∃δ=δ(ε)>0: ||Ax₁-Ax₂||<δ ⇒||x₁-x₂||<ε.

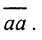
Пусть ∃ε>0: ∀δ>0∃x₁,x₂ ∈M:(||Ax₁-Ax₂||<δ ⇒||x₁-x₂||>ε).

Рассмотрим последовательность и пусть {δ_k}→ 0, а ||Ax_1k-Ax_2k||<δ_k, a ||x_1k-x_2k||≥ε. Так как множество М - компакт, то из последовательностей 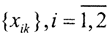можно выделить сходящиеся подпоследовательности {x_ikp}→x_i при p→∞, причём x₁≠x₂. Таким образом, ||Ax_1kp-Ax_2kp||→0 при p→∞, а x₁≠x₂. Противоречие. □

(Комментарий. Итак, минимизирующая последовательность {x_n} сходится к x_T, если:

Таким образом, при применении метода подбора требуется по-строить приближенное решение задачи Ax=f с некоторой гарантированной точностью по приближенным данным f_δ. При этом предполагается известной точность приближенных данных, т.е. максимальная величина отклонения приближенных данных, которыми мы располагаем, от абсолютно точных данных. Другими словами, для любых f_δ известно, что ||f-f_δ||<δ.)

Теорема 3. Если задача поставлена корректно по Тихонову, то есть x∈M_k, где M_k - компакт, то имеется принципиальная возможность построения такого решения x_ε, чтобы ∀x_ε>0 норма ||x_ε-x||≤ε.

□ Действительно, так как M - компакт, то можно построить конечную ε-сеть с элементами 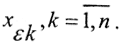. Выберем из элементов такой элемент x_εm, для которого величина ||Ax_εk-f_δ|| достигает минимального значения, то есть ||Ax_εm-f_δ||=min||Ax_εk-f_δ||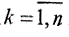

Полагая, что x_ε=x_εm, оценим норму ||x_ε-x||. Для этого рассмотрим элемент x_εp, существование которого следует из определения ε-сети и для которого ||x-x_εp||≤ε. Тогда ||Ax_εm-Ax||≤||Ax_εp-Ax||≤||A||*||x_εp-x||=||A||ε. □

(Комментарий. В качестве приближенного решения на множестве М уравнения Ax=y с приближенно известной правой частью y=y₁∈AM можно брать точное решение этого уравнения с правой частью y=y₁. Эта задача эквивалентна задаче нахождения на множестве M функции, миними-зирующей функционал F[x,y₁]=||Ax-y₁||² на соответствующем пространстве. Если ρ_Y(y_T,y₁)<δ, то в качестве приближенного решения уравнения Ax=y можно брать функцию x_δ, для которой ||Ax_δ-y₁||<δ.

Если, например, оператор A - интегральный, то интегральная сумма, полученная заменой правой части уравнения Ax=y значениями измеримой функции y на фиксированной сетке с n узлами, где значения искомой функции в узловых точках обозначены через x_i, будет системой линейных уравнений. Теперь задача построения приближенного решения уравнения Ax=y сведется к задаче нахождения конечномерного вектора, минимизирующего функционал F[x,y₁]=||Ax-y₁||² и удовлетворяющего неравенству ||Ax_δ-y₁||<δ.)

Приведенный метод построения приближенного решения по приближенным данным обладает большой общностью, он применим и к решению нелинейных операторных уравнений. Од-нако его применение обычно связано с очень большим объёмом вычислений, так как число n, как правило, быстро возрастает с уменьшением ε. Поэтому при решении некорректных задач часто применяются и другие методы.

Теорема Тихонова не содержит указаний на способы получения оценки устойчивости для конкретных задач. В некоторых простых и редких случаях можно получить теоретические оценки устойчивости.