2. Корректность по Фикера. Замкнутость

(Комментарий. Замкнутость можно сравнить с выравниванием линии фронта, то есть с отступлением от корректной разрешимости по Адамару на заранее подготовленные позиции.)

Определение 1. Линейный оператор А, действующий из банахова пространства X в банахово пространство Y, называется замкнутым, если для любой последовательности {x_n}∈D(A)⊂X и такой, что последовательность {x_n}→ x одновременно с последовательностью {Ax_n}→ y,причём элемент x∈D(A), а элемент y=Ax.

(Комментарий. Из определения следует, что если D(A)=X, то непрерывный линейный оператор всегда замкнут (НЛО всегда ЗЛО: "теорема о пришельцах"). Обратное, вообще говоря, неверно. То есть существуют замкнутые линейные операторы с областью определения, плотной в X, которые не являются непрерывными.)

Пример. Покажем, что оператор дифференцирования Dx(t) не ограничен, если действует изC[0,1] в C[0,1].

□ Рассмотрим операторное уравнение AX=Y в пространствах C[a,b]. Пусть оператор дифференцирования действует из C[0,1] в C[0,1], то есть операторное уравнение имеет вид Dx(t)=x'(t). Этот оператор определен не на всем пространстве непрерывных функций, а лишь на подпространстве непрерывных функций, имеющих непрерывную производную. Вообще, характерной особенностью разрывных операторов является то, что они не определены на всём пространстве.

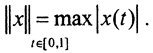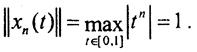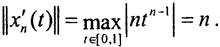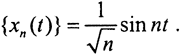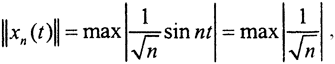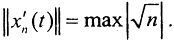В пространстве C[0,1] норма Возьмем из C[0,1] последовательность x_n(t)=tⁿ. Она ограничена в C[0,1]: Рассмотрим Dx_n(t)=x'_n(t)=nt^n-1.Тогда Таким образом, оператор D переводит ограниченное множество в неограниченное, то есть этот оператор не является ограниченным. Такая же ситуация с последовательностью В C[a,b] норма а Тогда 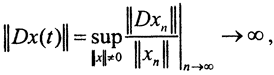то есть оператор дифференцирования Dx(t) не ограничен, то есть не является непрерывным. Это значит, что прямая задача некорректна на данной паре пространств C[a,b]→C[a,b]. □

Но если в пространстве исходных данных X выбрать более сильную норму, то ситуация изменится.

Рассмотрим пространство X как пространство C[a,b]⊂C[a,b], а пространство Y - как пространство C[a,b]. Тогда ||x(t)||_C¹[0,1]=max{max|x(t)|,max{|x'(t)|}=max{1, √n}= √n. Теперь 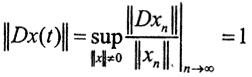и задача дифференцирования стала корректной, но на паре пространств C¹[a,b]→C[a,b].

На паре пространств C[a,b]→C[a,b] оператор дифференцирования является замкнутым, если область его определения есть C¹[a,b]. Действительно, пусть последовательность {x_n(t)}→x(t) в D(A)⊂X, D(A)=C¹[a,b]. Тогда последовательности {x_n(t)}→x(t) и {x'_n(t)}→y(t) сходятся равномерно на сегменте [a,b] и работает теорема о почленном дифференцировании последовательности функций. Отсюда 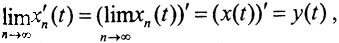то есть функция принадлежит области определения оператора Dx(t) и y=Dx. Но это и означает замкнутость оператора D.

(Комментарий. Заметим, что хотя на паре пространств C¹[a,b]→C[a,b] прямая задача дифференцирования корректна, обратная не корректна, так как оператор Dx(t) является вырожденным. Его ядро нетривиально и состоит из функций x(t)=c. Чтобы найти D^-1, нужно для любой функции y(t)∈C¹[a,b] решить уравнение Dx(t)=y(t). Но первообразная непрерывной функции определяется с точностью до постоянной - элемента из JerDx(t) оператора Dx(t). Поэтому обратный оператор не существует. Для того чтобы он существовал, то есть задача стала корректной, надо поставить задачу Коши. Определим, например, оператор Dx(t) на подпространстве C¹₀[0,1]⊂C¹[0,1] непрерывно дифференцируемых функций x(t), удовлетворяющих условию x(0)=0. Решение этой задачи Коши есть 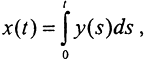, тогда )

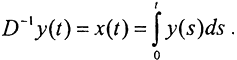Определение 2.Прямым произведением X*Y линейных пространств X и Y называют множество всех упорядоченных пар Z={z=(x,y)}, x∈X, y∈Y, причём z₁+z₂=(x₁+x₂,y₁+y₂), λz=(λx,λy). λ - произвольное число.

(Комментарий. Нетрудно видеть, что Z - линейное пространство. Если X и Y - нормированные пространства, то Z - нормированное пространство с нормой ||z||=||x||_X+||y||_Y.)

Определение 3. Пусть оператор A действует из банахова пространства X в банахово пространство Y. Графиком оператора A называется множество пар z=(x,Ax)∈Z, то есть ГрА⊂Z.

Определение 4. Пусть D(A) - линейное многообразие пространства X. График оператора A замкнут, если из того, что ∀{x_n}∈D(A):x_n→ x⇒{Ax_n}→y следует, что x∈D(A), а Ax=y.

Таким образом, линейный оператор A, действующий из D(A)⊂X в банахово пространство Y, замкнут, если его график есть замкнутое линейное подпространство пространства Z=X*Y.

Теорема1. Пусть 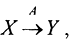где А - замкнутый линейный оператор, имеющий обратный оператор A^-1. Тогда A^-1 также является замкнутым.

□ График оператора A^-1 может быть получен из графика оператора А путем "перестановки" точек:ГрФ=(х,Ax)=(y,A^-1y)=ГрA^-1 - это одни и те же точки. □

Пример (продолжение). Посмотрим теперь на оператор дифференцирования как на обратный к оператору интегрирования Ax(t), заданному на паре пространств C[a,b]→C[a,b]. Равномерно сходящуюся последовательность функций всегда можно почленно интегрировать, то есть 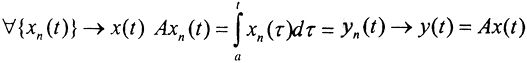и оператор интегрирования непрерывен. Тогда по "теореме о пришельцах" он замкнут. Обратным к нему является оператор дифференцирования, который замкнут согласно теореме1.

(Комментарий. Почти очевидно, что Z=X*Y - банахово пространство, если и только если X и Y банаховы. Если D(A)=X, то НЛО всегда ЗЛО. Когда верно обратное?)

Теорема2. (теорема Банаха о замкнутом графике). Пусть 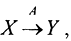где линейный оператор A, отображающий всё банахово пространство X на всё банахово пространство Y, имеет замкнутый график. Тогда A - линейный непрерывный оператор.

□ 1. Покажем, что ГрA есть подпространство Z=X*Y. Пусть (x₁,Ax₁)∈ГрA и (x₂,Ax₂)∈ГрA. Тогда их линейная комбинация λ₁((x₁,Ax₁))+λ₂(x₂,Ax₂)=(λ₁x₁,Aλ₁x₁)+(λ₂x₂,Aλ₂x₂)=(λ₁x₁+λ₂x₂)+A(λ₁x₁+λ₂x₂)∈ГрA. Поскольку А - ЗЛО по условию, то ГрA замкнут в X*Y, то есть это подпространство.

2. На подпространстве ГрA⊂X*Y (замкнутое подпространство банахова пространства само является банаховым пространством). Рассмотрим оператор проецирования P, действующий по правилу ∀ (x,Ax)∈ГрA P(x,Ax)=x. Это линейный оператор, так как λ₁((x₁,Ax₁))+λ₂(x₂,Ax₂)=(λ₁x₁,Aλ₁x₁)+(λ₂x₂,Aλ₂x₂)=(λ₁x₁+λ₂x₂)+A(λ₁x₁+λ₂x₂)∈ГрA. Таким образом, оператор P биективно отображает банахово пространство ГрA на банахово пространство X. Покажем, что он непрерывен: ||P||=||P(x,Ax)||=||x||=sup_||x||≤1||x||≤1. Тогда по теореме Банаха о гомеоморфизме существует непрерывный линейный обратный оператор P^-1: ||P^-1x||=||(x,Ax)||=||x||+||Ax||≥||Ax||, то есть ||Ax||≤||P^-1x||⇒||A||≤||P^-1||. Тогда A - линейный непрерывный оператор. □

(Комментарий. Для оператора A, отображающего всё банахово пространство X на всё банахово пространство Y, понятия замкнутости и непрерывности совпадают. Выясним, при каких условиях эти понятия совпадают, если D(A)⊂X.)

Теорема3. Критерий замкнутости линейного оператора. Пусть 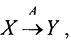где пространства X и Y банаховы. Линейный непрерывный оператор А замкнут, если и только если множество D(A)⊂X замкнуто.

□ Необходимость. Пусть оператор A - НЛО и множество D(A)⊂X замкнуто. Покажем, что A замкнут. Рассмотрим последовательность x_n∈D(A):{x_n}→x, {Ax_n}→y. Так как множество D(A)⊂X замкнуто, x∈D(A), а из того, что оператор непрерывен, следует, что Ax=y, что и означает замкнутость оператора A.

Достаточность. Пусть оператор A - НЛО и замкнут. Покажем, что множество D(A)⊂X замкнуто. Пусть {x_n}→x, x_n∈D(A), а x - предельная точка D(A). Тогда ||Ax_p-Ax_q||≤||A||*||x_p-x_q||, то есть последовательность {Ax_n} фундаментальна. Так как пространство Y банахово, то последовательность {Ax_n}→y, а из замкнутости оператора A следует, что Ax=y. □

Теорема 4 (Фикера)Критерий разрешимости уравнения. Ax=y. Пусть 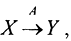где пространства X и Y банаховы, оператор А-биективный НЛО, причём D(A)=X, а R(A)⊂Y. Тогда ||A^-1||<∞, если и только если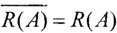

□ Необходимость. Пусть ||A^-1||<∞. Так как оператор A - НЛО и множество D(A)=X замкнуто, то по теореме 3 оператор A замкнут. Тогда по теореме 1 оператор A^-1, существующий в силу биективности оператора A, тоже замкнут и непрерывен по условию. Но D(A^-1)=R(A). Тогда по теореме 3 множество R(A) замкнуто, то есть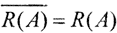

Достаточность. Пусть 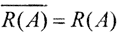Тогда линейный непрерывный оператор А отображает всё банахово пространство X на банахово пространство R(A), то есть по теореме Банаха о гомеоморфизме оператор A^-1 непрерывен, то есть ||A^-1||<∞. □

(Комментарий. Если оператор A обратим, то операторная устойчивость задачи, то есть существование ограниченного обратного оператора A^-1, равносильно замкнутости множества R(A). Если множество R(A) не замкнуто, то оператор A^-1 разрывен. Если оператор A^-1 разрывен, множество R(A) не замкнуто.)

Определение 5. Задача решения уравнения Ax=y корректно разрешима по Фикера, если множество значений оператора R(A) замкнуто.

(Комментарий. Замкнутое подмножество банахова пространства есть банахово пространство, то есть для замкнутых операторов множества D(A) и R(A) становятся банаховыми пространствами и на них восстановлены все условия корректности по Адамару. Это и называется корректностью по Фикера.)

Определение 6. Говорят, что незамкнутый оператор А допускает замыкание A^-, если его можно расширить до замкнутого оператора по правилу ∀x_n∈D(A):x_n→x, Ax_n→y верно, что A^-x=y.

Можно показать, что для этого необходимо и достаточно, чтобы ∀{x_n}∈D(A):x_n→0, Ax_n→y⇒y=0.

Определение 7. Задача решения уравнения Ax=y обобщённо разрешима, если оператор A допускает замыкание. Решения уравнения A^-x=y называют обобщенными решениями уравнения Ax=y.

Пример. Оператор Ax=x'(0) незамыкаем как фунционал на непрерывно дифференцируемых функциях на C[01]. Действительно, последовательность 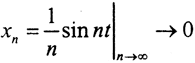равномерно на [0,1], а последовательность Ax_n=const|_t=0=1.

Если операторное уравнение Ax=y неразрешимо, потому что оператор A не допускает замыкания, то это уравнение в гильбертовом пространстве заменяется на нормальное уравнение A*Ax=A*y. Это уравнение мы рассмотрим ниже. Можно показать, что нормальный оператор A*A допускает замыкание.