
3. Корректность компактных операторов
Определение. Линейный оператор A, отображающий банахово пространство E в себя (или другое банахово пространство), называется компактным (вполне непрерывным), если каждое ограниченное множество он переводит в предкомпактное.
(Комментарий. Напомним, что множество M метрического пространства X компактно, если из любого бесконечного его подмножества можно выделить последовательность, сходящуюся к элементу из M, и предкомпактно, если замыкание M_ компактно. Если линейный оператор A компактен, то он переводит любую ограниченную последовательность {xn} в компактную последовательность {Axn}, то есть из любой подпоследовательности последовательности {Axn} можно выделить сходящуюся подпоследовательность. Компактность и предкомпактность - это прежде всего свойства пространств. Суть компактности - в исчерпываемости некого бесконечномерного пространства конечномерным приближением с любой наперед заданной точностью. Компактный оператор наследует свойства конечномерного оператора в том смысле, что всегда может быть приближен им.)
Теорема1. Компактный оператор всегда ограничен.
□ 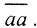 Пусть компактный оператор A не ограничен. Тогда найдется последовательность {xn}, такая, что ||Axn||≥n|. Но тогда из неё нельзя выделить сходящуюся подпоследовательность, что противоречит тому, что A - вполне непрерывный оператор. □
Пусть компактный оператор A не ограничен. Тогда найдется последовательность {xn}, такая, что ||Axn||≥n|. Но тогда из неё нельзя выделить сходящуюся подпоследовательность, что противоречит тому, что A - вполне непрерывный оператор. □
(Комментарий. Не любой непрерывный линейный оператор вполне непрерывен. Рассмотрим, например, единичный оператор I:L2[a,b]→L2[a,b]:Ix=x ∀ x∈L2[a,b]. Он, очевидно, ограничен, но не компактен. Покажем это.
□ В пространстве L2[a,b] существует бесконечная ортонормированная система (ОНС) 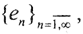 такая, что
такая, что 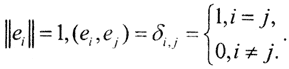 Ясно, что последовательность {en} лежит на сфере S_(0,1), то есть она ограничена, но из неё нельзя выделить сходящуюся подпоследовательность, так как ||ei-ej||2=(ei-ej,ei-ej)=2. То есть единичная сфера S_(0,1) в гильбертовом пространстве - замкнутое и ограниченное множество, но не компакт, а IS_(0,1)=S_(0,1). Таким образом, единичный оператор I не компактен. □
Ясно, что последовательность {en} лежит на сфере S_(0,1), то есть она ограничена, но из неё нельзя выделить сходящуюся подпоследовательность, так как ||ei-ej||2=(ei-ej,ei-ej)=2. То есть единичная сфера S_(0,1) в гильбертовом пространстве - замкнутое и ограниченное множество, но не компакт, а IS_(0,1)=S_(0,1). Таким образом, единичный оператор I не компактен. □
Можно показать, что единичный оператор I в любом бесконечномерном банаховом пространстве не компактен. Это следует из теоремы Рисса о некомпактности единичного шара в бесконечномерном - пространстве.)
Теорема2. Если A - компактный оператор, B - ограниченный в банаховом пространстве X, то операторы AB и BA - компактны.
□ Если множество M⊂X ограничено, то множество BM тоже ограничено. Следовательно, множество ABM предкомпактно, а это и означает, что оператор AB компактен. Далее, если M⊂X ограничено, то AM предкомпактно, а тогда в силу непрерывности B множество BAM тоже предкомпактно, то есть оператор BA компактен. □
В качестве основного примера линейного оператора рассмотрим оператор Фредгольма в пространстве L2[a,b], сопоставляющий функции u(x) новую функцию Au=f(x), определенную с помощью формулы 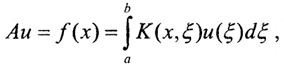 где K(x,ξ) - некоторая непрерывная функция двух переменных. Оператор A называется интегральным, его линейность очевидна из линейности интеграла. Если ядро K(x,ξ) непрерывно по совокупности аргументов, то в соответствии с теоремой о непрерывной зависимости от параметра собственного интеграла, оператор A действует в линейном функциональном пространстве.
где K(x,ξ) - некоторая непрерывная функция двух переменных. Оператор A называется интегральным, его линейность очевидна из линейности интеграла. Если ядро K(x,ξ) непрерывно по совокупности аргументов, то в соответствии с теоремой о непрерывной зависимости от параметра собственного интеграла, оператор A действует в линейном функциональном пространстве.
Теорема 3. Оператор Фредгольма непрерывен в пространствах C[a,b] и L2[a,b].
□ 1. Покажем, что оператор Фредгольма непрерывен в пространстве C[a,b].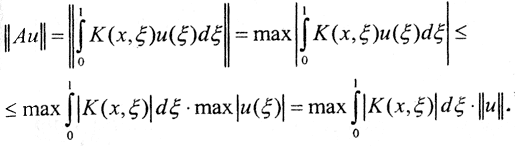 Таким образом,
Таким образом, 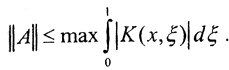 Но
Но 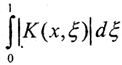 - непрерывная и, следовательно, ограниченная на сегменте [0,1] функция, то есть и
- непрерывная и, следовательно, ограниченная на сегменте [0,1] функция, то есть и 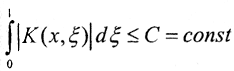 □
□
2. Покажем, что оператор Фредгольма ограничен и, следовательно, непрерывен в пространстве L2[a,b]. По неравенству Коши Буняковского для каждого фиксированного x∈[0,1], полагая, что 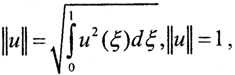 можно записать
можно записать 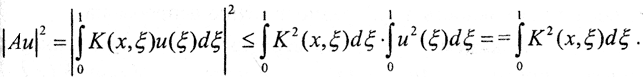 Интегрируем по x:
Интегрируем по x: 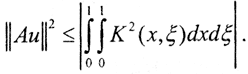 Правая часть неравенства не зависит от u и ограниченна, поэтому
Правая часть неравенства не зависит от u и ограниченна, поэтому 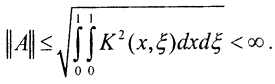 □
□
Теорема 4. Пусть функция K(x,ξ) непрерывна на квадрате x,ξ∈[a,b]. Тогда интегральный оператор Фредгольма 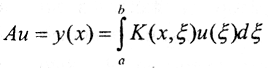 компактен в пространствах C[a,b] и L2[a,b].
компактен в пространствах C[a,b] и L2[a,b].
□ Докажем сначала компактность интегрального оператора Фредгольма в пространстве C[a,b]. Рассмотрим последовательность un∈L2[a,b].:||un||≤M и последовательность 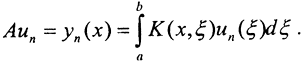 .
.
1. Покажем равностепенную непрерывность последовательности Aun=yn(x). На квадрате x,ξ∈[a,b] функция K(x,ξ) равномерно непрерывна по теореме Кантора, так как она непрерывна на замкнутом и ограниченном множестве в R2. Значит, 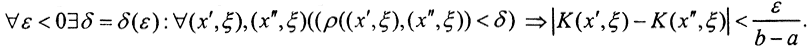 Оценим разность: |Δyn|=|yn(x')-yn(x")| при ρ((x',ξ),(x",ξ))<δ:
Оценим разность: |Δyn|=|yn(x')-yn(x")| при ρ((x',ξ),(x",ξ))<δ: 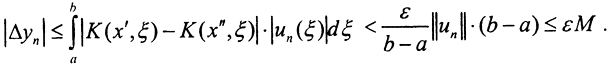 То есть последовательность yn(x) равностепенно непрерывна.
То есть последовательность yn(x) равностепенно непрерывна.
2. Покажем равномерную ограниченность последовательности Aun=yn(x). Пусть 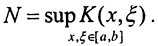 Тогда
Тогда 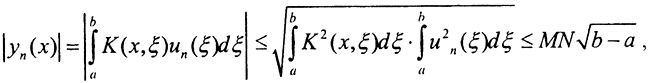 а это и есть равномерная ограниченность. Итак, множество функций y(x)∈C[a,b] равномерно ограничено и равностепенно непрерывно, то есть в соответствии с критерием Арцела оператор A является вполне непрерывным в пространстве C[a,b]. Но, так как из равномерной сходимости следует сходимость в среднем, оператор A является вполне непрерывным и при действии из L2[a,b] в L2[a,b]. □
а это и есть равномерная ограниченность. Итак, множество функций y(x)∈C[a,b] равномерно ограничено и равностепенно непрерывно, то есть в соответствии с критерием Арцела оператор A является вполне непрерывным в пространстве C[a,b]. Но, так как из равномерной сходимости следует сходимость в среднем, оператор A является вполне непрерывным и при действии из L2[a,b] в L2[a,b]. □
Теорема5. Интегральный оператор Фредгольма 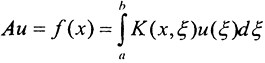 не имеет ограниченного обратного. □
не имеет ограниченного обратного. □
Рассмотрим единичный шар B_(0,1) в гильбертовом пространстве. Шар B_(0,1) - замкнутое и ограниченное множество, но не компакт. Подействуем на него оператором A. Если A - компактный оператор, то AB_(0,1) - компакт. Если A-1 ограничен, то шар A-1AB_(0,1)=B_(0,1) - компакт или предкомпакт, что противоречит некомпактности единичного шара. □
(Комментарий. Итак, задача может оказаться корректной в одной паре пространств и некорректной в другой. Но некорректность интегрального уравнения Фредгольма первого рода не зависит от выбора пространств и устанавливается от противного: если задача корректна, то существует непрерывный оператор A-1, и, следовательно, тождественный оператор I=A-1A компактен в соответствующем бесконечномерном пространстве, что невозможно.)
Теорема 6. Вполне непрерывный оператор A:U→F имеет замкнутое множество значений R(A) тогда и только тогда, когда R(A) конечномерно.
□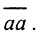 Пусть A - вполне непрерывный оператор, R(A) замкнуто и бесконечномерно. Тогда в силу теоремы 4 из пункта 2 существует ограниченный обратный оператор A-1, определенный на всем R(A), и поэтому произведение A-1A=I будет также вполне непрерывным оператором. Это противоречит теореме Рисса о некомпактности единичного шара в бесконечномерном пространстве. Обратное утверждение очевидно. □
Пусть A - вполне непрерывный оператор, R(A) замкнуто и бесконечномерно. Тогда в силу теоремы 4 из пункта 2 существует ограниченный обратный оператор A-1, определенный на всем R(A), и поэтому произведение A-1A=I будет также вполне непрерывным оператором. Это противоречит теореме Рисса о некомпактности единичного шара в бесконечномерном пространстве. Обратное утверждение очевидно. □
Пример. Покажем, что оператор дифференцирования 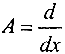 не компактен при действии C1[0,1]→C[0,1] и компактен при действии C2[0,1]→C[0,1].
не компактен при действии C1[0,1]→C[0,1] и компактен при действии C2[0,1]→C[0,1].
□ 1. Рассмотрим в пространстве C1[a,b] последовательность 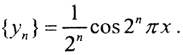 Эта последовательность ограничена в C1[0,1], так как ∀n∈N
Эта последовательность ограничена в C1[0,1], так как ∀n∈N 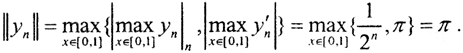 Однако последовательность образов ее элементов {Ayn}=πsin2nπx некомпактна в пространстве C1[0,1]. Чтобы это показать, рассмотрим ||yn(x)-ym(x)||≥|yn(x0)-ym(x0)| ∀x0 ∈[0,1]. Выберем
Однако последовательность образов ее элементов {Ayn}=πsin2nπx некомпактна в пространстве C1[0,1]. Чтобы это показать, рассмотрим ||yn(x)-ym(x)||≥|yn(x0)-ym(x0)| ∀x0 ∈[0,1]. Выберем 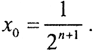 . Тогда при ,=n+1+k видно, что |yn(x0)-ym(x0)|=π, то есть ни сама последовательность, ни любая её подпоследовательность даже не фундаментальны. Поэтому оператор дифференцирования не является компактным при действии C1[0,1]→→C[0,1].
. Тогда при ,=n+1+k видно, что |yn(x0)-ym(x0)|=π, то есть ни сама последовательность, ни любая её подпоследовательность даже не фундаментальны. Поэтому оператор дифференцирования не является компактным при действии C1[0,1]→→C[0,1].
2. Рассмотрим случай C2[0,1]→→C[0,1]. Пусть {yn(x)} - произвольная ограниченная последовательность в пространстве C2[0,1], то есть 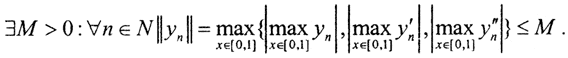 Ясно, что
Ясно, что 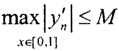 и
и 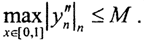 Последовательность
Последовательность 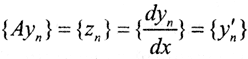 состоит из равномерно ограниченных непрерывных функций. Более того, последовательность {zn} равностепенно непрерывна. Действительно, так как
состоит из равномерно ограниченных непрерывных функций. Более того, последовательность {zn} равностепенно непрерывна. Действительно, так как 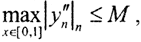 то ∀ε>0 найдётся такое δ=δ(ε)>0, что
то ∀ε>0 найдётся такое δ=δ(ε)>0, что 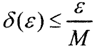 Поэтому ∀x1x2∈[0,1]:|x1-x2|≤δ ⇒|yn"|*|x1-x2|≤Mδ≤ε. Это и означает, что последовательность не только равномерно ограниченна, но и равностепенно непрерывна, то есть компактна по критерию Арцела.
Поэтому ∀x1x2∈[0,1]:|x1-x2|≤δ ⇒|yn"|*|x1-x2|≤Mδ≤ε. Это и означает, что последовательность не только равномерно ограниченна, но и равностепенно непрерывна, то есть компактна по критерию Арцела.
(Комментарий. Таким образом, на паре пространств C2[a,b]→C[a,b] прямая задача дифференцирования корректна, обратная не корректна, так как оператор Dx(t) становится компактным и поэтому не имеет ограниченного обратного.)
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'