
2. Вычисление норм невырожденных матриц
Рассмотрим для простоты преобразование двумерного пространства X в двумерное пространство Y оператором A, причём матрица линейного оператора A невырожденна и имеет вид 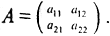
1. Рассмотрим преобразование R22→ R22, где точки M1(x1,x2), M2(x'1,x'2)∈ X, а точки N1(y1,y2), N2(y'1,y'2)∈Y. Тогда y1=a11x1+a12x2, а y2=a21x1+a22x2. Обозначим Δx1+x1-x'1, Δx2=x2-x'2. Тогда ρ2(N1,N2)=(a11Δx1+a12ΔxΔ2)2+(a21Δx1+a22Δx2)2. Запишем это как скалярное произведение и воспользуемся неравенством Буняковского Коши. 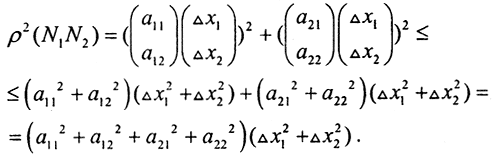 Тогда ρ(N1,N2)≤(a112+a122+a212+a222)1/2ρ(M1M2), то есть
Тогда ρ(N1,N2)≤(a112+a122+a212+a222)1/2ρ(M1M2), то есть 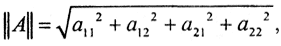 а норма
а норма 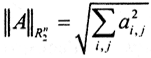 называется эвклидовой.
называется эвклидовой.
2. Рассмотрим преобразование R12→ R21.
ρ(N1,N1)=|y1-y'1|+|y2-y'2|=|Δy1|+|Δy2|=|a11Δx1+a12Δx2|+|a21Δx1+a22Δx2|≤(|a11|+|a21|)|Δx1|+(|a12|+|a22|)|Δx2|≤max{|a11|+|a21|,|a12|+|a22|}ρ(M1,M2), ||A||1=max{|a11|+|a21|,|a12|+|a22|}. Такая норма называется столбиковой.
3. Рассмотрим преобразование R∞2→ R2∞.
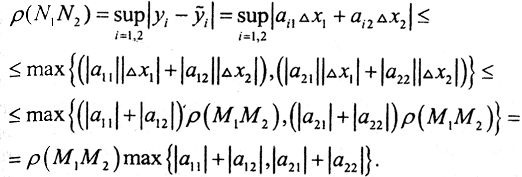
Тогда ||A||∞=max{|a11|+|a12|,|a21|+|a22|}.
Такая норма называется строчной.
Таким образом, нормы матриц согласованы (аффелированы) с нормами векторов в соответствующих пространствах. С конечномерным эвклидовым пространством аффелирована ещё одна норма, которая называется спектральной.
(Комментарий. Пусть непрерывный линейный оператор A определен в (вообще говоря, бесконечномерном) комплексном гильбертовом пространстве. Наряду с уравнением Ax=λx рассмотрим уравнение (A-λI)x=y. При этом в трактовке спектра возникают существенные отличия бесконечномерного случая от конечномерного. Если оператор (A-λI) не обратим, то есть оператор (A-λI)-1 не существует, то в пространстве H существует ненулевой вектор x, такой, что Ax=λx. В таком случае число λ называют собственным значением оператора A, а вектор x - собственным вектором оператора A, отвечающим собственному значению λ. Совокупность всех собственных значений оператора A называют точечным спектром σp(A) оператора A. В конечномерном пространстве спектр оператора может быть только точечным, потому что если матрица Am*n оператора (A-λI) обратима, то обратная к ней матрица задает оператор (A-λI)-1 сразу во всем пространстве. Тогда оператор (A-λI)-1, определенный во всем пространстве H, называется резольвентой оператора A и обозначается Rλ, а комплексное число λ называется регулярным значением оператора A. В бесконечномерном пространстве число λ называется регулярным значением оператора А, если резольвента (A-λI)-1 существует, ограничена и определёна на всём пространстве. Совокупность всех комплексных чисел λ, не являющихся регулярными значениями оператора A, называется спектром σp(A) оператора A, то есть к спектру относятся все нерегулярные значения операторной резольвенты (A-λI)-1. Теперь спектр и собственные значения - это не одно и то же. Не все из них соответствуют собственным значениям, определяемым уравнением Ax=λx. Интегральный оператор свертки вообще не имеет собственных значений, поскольку выходной сигнал динамической системы не повторяет входного. Спектр может быть непрерывным. В ряде случаев точечный спектр сгущается, имеют место предельные точки. Ясно, что если λ∈σ(A), то задача с уравнением (A-λI)x=y некорректна: она либо имеет неединственное решение, либо разрешима не для всякой правой части, либо у неё нет непрерывной зависимости от правой части.)
Теорема 1. Норма оператора 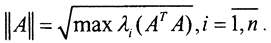
□Норма оператора 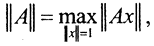 где x={x1,x2,...,xn}. Тогда эвклидова норма в пространстве Rn2
где x={x1,x2,...,xn}. Тогда эвклидова норма в пространстве Rn2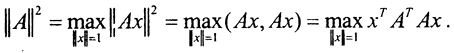 Теперь задача свелась к нахождению максимума функции f(x)=f(x1,x2,...,xn}=xTATAx при условии x12+x22+...+x2n=1. Будем искать точку безусловного максимума функции Лагранжа L(x1,x2,...,xn,λ)=f(x1,x2,...,xn)-λ(x12+x22+...+xn2-1)=xTATAx-λ(xTx-1).
Теперь задача свелась к нахождению максимума функции f(x)=f(x1,x2,...,xn}=xTATAx при условии x12+x22+...+x2n=1. Будем искать точку безусловного максимума функции Лагранжа L(x1,x2,...,xn,λ)=f(x1,x2,...,xn)-λ(x12+x22+...+xn2-1)=xTATAx-λ(xTx-1).
В точке безусловного максимума дифференциал функции равен нулю. Для функций xTATAx и (xTx-1) дифференциал можно получить прямо по его определению, как главную линейную часть приращения функции (в главе VII будет развита другая техника):
Δf=f(x+Δx)-f(x)=(x+Δx)TATA(x+Δx)-xTATAx=2xTATAΔx+ΔxTATAΔx=2xTATAΔx+o(|Δx|).
Метод Лагранжа дает для любых Δx систему уравнений 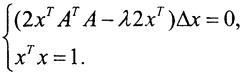 Или
Или  Это означает, что x - собственный вектор матрицы ATA, имеющий единичную длину; λ - собственное число матрицы ATA. Другими словами, максимум функции (Ax,Ax)=xTATAx на единичной сфере (x,x)=xTx=1 достигается на одном из собственных векторов матрицы ATA, и он равен корню из собственного числа λ этой матрицы. Поэтому, для отыскания спектральной нормы матрицы A, аффелированной с эвклидовой нормой в пространстве Rn2, следует найти все собственные числа λk матрицы ATA, и корень из наибольшего из них является искомой нормой. Для действительных матриц ATA=A*A. То есть норма оператора
Это означает, что x - собственный вектор матрицы ATA, имеющий единичную длину; λ - собственное число матрицы ATA. Другими словами, максимум функции (Ax,Ax)=xTATAx на единичной сфере (x,x)=xTx=1 достигается на одном из собственных векторов матрицы ATA, и он равен корню из собственного числа λ этой матрицы. Поэтому, для отыскания спектральной нормы матрицы A, аффелированной с эвклидовой нормой в пространстве Rn2, следует найти все собственные числа λk матрицы ATA, и корень из наибольшего из них является искомой нормой. Для действительных матриц ATA=A*A. То есть норма оператора  .
.
(Комментарий. Для любой вещественной матрицы A собственные числа матрицы ATA неотрицательны, так как ||Ax||2=|Ax|2=(Ax)2=(Ax,Ax)=xTATAx. Каждая вещественная квадратичная форма приводится к сумме квадратов, коэффициентами которых являются собственные числа симметричной части матрицы. Поэтому для неотрицательной квадратичной формы xTATAx с симметричной матрицей ATA собственные числа последней отрицательными быть не могут.)
Определение.Сингулярными числами матрицы A называются действительные неотрицательные числа 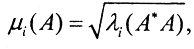
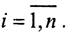 обычно расположенные в порядке невозрастания.
обычно расположенные в порядке невозрастания.
Если матрица ATA=A*A вырожденна и имеет ранг r<n, то μ1≥μ2≥μ3...≥μr>μr+1=...μn=0, а если матрица ATA невырожденна, то μ1≥μ2≥μ3...≥μn>0
Теорема 2. Пусть самосопряжённый оператор A задан в пространстве Rn2. Тогда ||A||=|λmax|.
□ Разложим x по базису собственных векторов 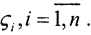 Тогда x=∑aiςi и, по определению нормы,
Тогда x=∑aiςi и, по определению нормы, 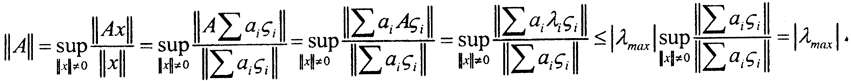
С другой стороны, заменив вектор x на вектор ςmax, мы только уменьшим его, то есть 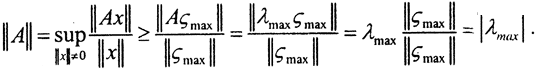 То есть ||A||=|λmax| - спектральная норма.□
То есть ||A||=|λmax| - спектральная норма.□
(Комментарий. Если A - самосопряжённый оператор, то матрица вещественна и симметрична. Самосопряжённый вполне непрерывный оператор А имеет хотя бы одно собственное значение, причём в Н можно выбрать полную ортогональную систему элементов, состоящую из собственных функций оператора А. Тогда, по теореме о приведении квадратичной формы каноническому виду, в ортонормированном базисе из собственных векторов симметричная матрица имеет диагональный вид, причем на диагонали стоят ее собственные числа. То есть норма симметричной вещественной матрицы равна максимуму из модулей её собственных чисел.)
Теорема 3. Собственные значения матрицы A-1 обратны собственным значениям матрицы , а собственные векторы этих матриц совпадают.
□ Равенство Aςi=λiςi умножим слева на A-1: 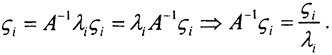 Это заодно показывает, что собственные векторы совпадают.□
Это заодно показывает, что собственные векторы совпадают.□
Теперь condA самосопряжённого оператора можно вычислить из теоремы 2, так как 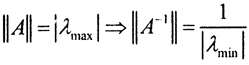 и сразу
и сразу 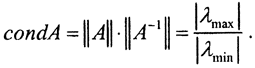
(Комментарий. Можно показать, что:
- справедливо равенство
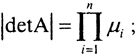
- собственные значения квадратной матрицы A, вообще говоря, комплексны, но если A симметрична, то все её собственные значения действительны;
- если A симметрична и положительна, то все собственные значения действительны и неотрицательны;
- все сингулярные числа μ любой матрицы действительны, неотрицательны и при этом во всех случаях могут иметь кратность, доходящую до n.
Если A - квадратная невырожденная матрица, то для нахождения condA вместо собственных значений используются сингулярные числа μ: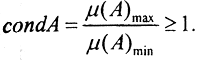 )
)
Пример. Рассмотрим систему 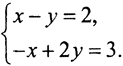 1. Найти эвклидову, столбиковую, строчную и спектральную нормы.
1. Найти эвклидову, столбиковую, строчную и спектральную нормы.
2. Во всех случаях найти condA=||A||*||A-1||. Матрица оператора 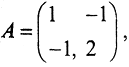 , тогда
, тогда 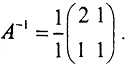 Эвклидова норма:
Эвклидова норма: 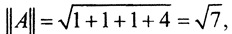
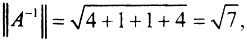 condA=7.
condA=7.
Строчная норма:
||A||=max{2,3}=3, ||A-1||=max{3,2}=3, condA=9.
Столбиковая норма:
||A||=max{2,3}=3, ||A-1||=max{3,2}=3, condA=9.
Спектральная норма: 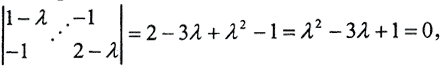
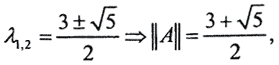
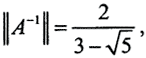 тогда
тогда 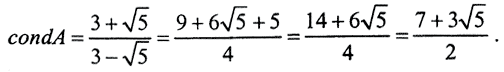
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'