1. Обусловленность СЛАУ. Число обусловленности матрицы

Для корректной постановки задачи требуется существование и единственность решения, а также непрерывная зависимость решения от входных данных. Рассмотрим обратную задачу Ax=y для СЛАУ. Если A^-1≠0, то решение задачи существует и единственно. Входными данными в этом случае являются коэффициенты матрицы линейного оператора A и правая часть. Пусть и матрица, и правая часть невырожденной системы Ax=y заданы с некоторой погрешностью. Наряду с системой Ax=y рассмотрим СЛАУ (A+ΔA)*(x+Δx)=y+Δy.

Определение. Обратная задача для СЛАУ Ax=y устойчива по правой части, если для любых справедлива оценка ||Δx|| ≤C||Δy||, где C - постоянная, независящая от правой части.

Эта оценка выражает факт непрерывной зависимости решения от правой части, т.е. показывает, что ||≤x||→0 при ||≤y||→0.

Получим оценку относительной погрешности решения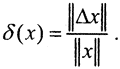

□ Ясно, что Δx=A^-1(ΔΔy-ΔAx-ΔAΔx). Тогда, использовав неравенство треугольника, получаем ||Δx||||A^-1||||Δy||+||A^-1||||ΔA||||x||+||A^-1||||ΔA||||Δx||, или 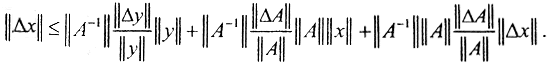Обозначим τ(A)=condA=||A^-1||*||A||. Тогдa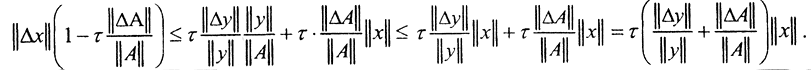

Заметим, что 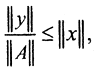так как ||y||=||Ax||≤||A||*||x||. Тогда для оценки относительной погрешности решения окончательно получим 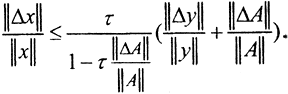Обозначим 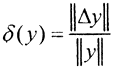относительную ошибку измерения, 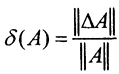- относительную ошибку задания оператора. Величина τ(A)=condA=||A^-1||*||A|| называется числом обусловленности Тьюринга матрицы A (коэффициентом усиления ошибки). Тогда 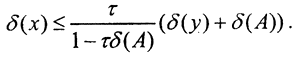При ΔA=0 получаем оценку при наличии погрешности только правых частей δ(x)≤τδ(y). □

(Комментарий. В результате получено соотношение, показывающее, на сколько возрастают относительные ошибки решения СЛАУ в случае наличия относительных ошибок при задании правых частей и элементов матриц. Это неулучшаемая оценка для относительной ошибки решения, которая, конечно, может быть существенно завышенной. Ясно, что τ(A)=||A^-1||||A||≥||A^-1A||=||E||=1 , то есть для любой матричной нормы число обусловленности не меньше единицы. Большие значения числа обусловленности отвечают матрицам, плохо обращаемым численными методами. Для нормированных матриц (то есть матриц, у которых ||A||=1) это означает наличие в обратной матрице больших элементов, и, следовательно, малые изменения правой части могут привести к относительно большим (хотя и конечным) изменениям в решении. Поэтому системы с плохо обусловленными матрицами практически неустойчивы, хотя задача корректна и выполнено условие устойчивости ||A^-1||<∞. Если condA<10, то говорят, что СЛАУ хорошо обусловлена, то есть ошибки входных данных слабо влияют на решение. Если condA>10³,то СЛАУ обусловлена плохо, что приводит к большим, но конечным изменениям в решении. Плохая обусловленность не следствие малости по сравнению с единицей определителя А и не оттого, что знаменатель мал или обратная матрица близка к 0, а за счёт появления в обратной матрице больших членов. Появляется класс "почти вырожденных операторов". Можно привести пример, где определитель матрицы будет не мал по сравнению с коэффициентами. Рассмотрим диагональную матрицу A_20*20 у которой все диагональные элементы равны 10 и диагональную матрицу A'_20*20, у которой все диагональные элементы равны 10, кроме последнего, равного 10^-18. Тогда detA=10²⁰, а detA'=10¹⁹*10^-18=10, condA=1, condA'=10¹⁹. Ошибка в 10^-18 резко меняет поведение системы (точность в физике до 10^-12-10^-13, в астрономии до 10^-6, в технике до 10^-3, в психологии от10%).)

Пример. Рассмотрим СЛАУ 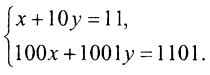Её решение {x,y}={1,1}. Однако решение СЛАУ 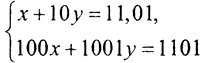уже {x,y}={11,01;0}, то есть погрешность решения существенно больше, погрешности определения коэффициента. Для матрицы 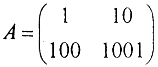обратная матрица имеет вид 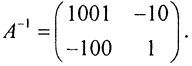Тогда число обусловленности condA, вычисленное, например, по строчной норме, оказывается равным более 10⁶.