3. Плохая обусловленность и некорректность

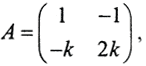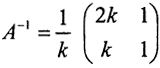
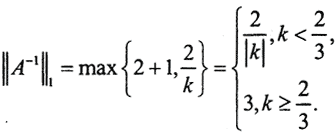Исследуем зависимость числа обусловленности condA от соотношения коэффициентов матрицы. Если умножить второе уравнение СЛАУ впредыдущем примере на k, то её решение от этого не изменится, но condA станет функцией от k. Так как то Число обусловленности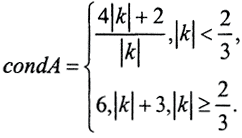

Число обусловленности изменяется при умножении на k, хотя умножение строки системы на число задачу не меняет. 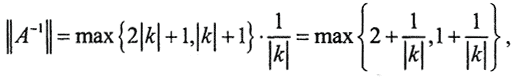то есть 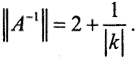Таким образом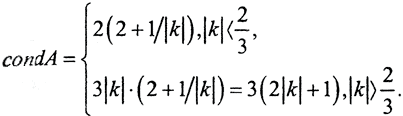

В случае спектральной нормы 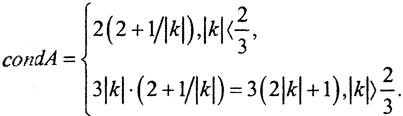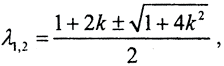то есть 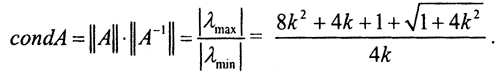График зависимости condA от параметра имеет вид:

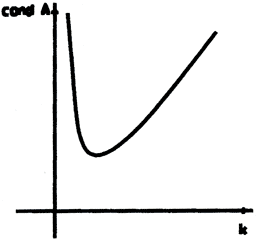
(Комментарий. Качественно характер графика очевиден. При k→0 или при k→∞ строчка или столбец матрицы стремятся к нулю, то есть матрица "стремится" к вырожденной, у которой число Тьюринга бесконечно. Следовательно, существует такое значение k, при котором условия (conditions) для решения СЛАУ "наиболее благоприятны".)

Число обусловленности характеризует априорную оценку сверху, то есть наихудшую оценку возможных ошибок решения СЛАУ. Сделаем апостериорную оценку. Пусть при решении СЛАУ Ax=b получено решение x_p. Тогда вектор невязки будет иметь вид δ=Ax_p-b. Так как ||b||=||Ax||≤||A||*||x||, откуда 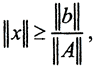а A^-1δ=x_p-A^-1b=x_p-x и ||x_p-x||≤||A^-1||*||δ||, ясно, что 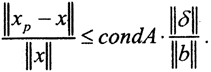Видно, что апостериорная оценка точности решения не лучше. Показано, что и вероятностные оценки точности решения близки к априорным. Таким образом, число обусловленности даёт реальную оценку сверху возможных ошибок решения. Можно показать, что нормализация СЛАУ, то есть переход от заданной СЛАУ Ax=b к равносильной системе уравнений A*A не улучшает обусловленность матрицы . Кроме того, имеет место следующий факт. Пусть матрица A диагонализируема, то есть =T^-1ΛT, Λ=diag{λ_i}, 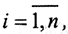T - матрица-трансформер. Тогда для любого λ_h - собственного значения возмущённой матрицы A_h=A+hA найдётся собственное значение λ_i матрицы A, такое, что |λ_h-λ_i|≤||T||*||T^-1||*||hA||=condA*||hA||.

Таким образом, число обусловленности характеризует наихудшую оценку влияния возмущения матрицы на её спектр.

Пример 3. Проиллюстрируем некорректность и плохую обусловленность на примере СЛАУ 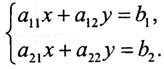Этот пример предложил А.Н.Тихонов. Рассмотрим вырожденную СЛАУ: 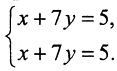Её решение {x,y}={5-7t,t}, t∈ R. То есть, эта СЛАУ некорректна в смысловом поле конкретной задачи. А.Н. Тихонов рассматривает систему, первое уравнение которой имеет вид x+7y=5, а второе получается из первого умножением его на 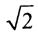: 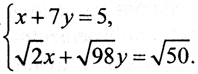Далее вычисляется 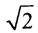с точностью до: 1) 10^-5; 2) 10^-6; 3) 10^-50; 4) 10^-200. В результате получается: и так далее. В этих случаях получаются следующие значения для x:

1) x=2,0; 2)x=-1,33333; 3)x=9,6666; 4)x=-5,50... При точности в 100, 300 и 500 десятичных знаков компьютер выдаёт следующие результаты: x⁽¹⁰⁰⁾=0,0...; x⁽³⁰⁰⁾=1,6...; x⁽⁵⁰⁰⁾=5,0....

Если вычисления производятся с конечной точностью, то отличить вырожденные и плохо обусловленные системы невозможно. Поэтому говорят о практической некорректности СЛАУ и применяют одинаковые методы борьбы с ней.