3. Пространства операторов

Пусть X и Y - линейные нормированные пространства, оба вещественные или оба комплексные.

Определение 1. Оператор А ограничен, если ∀x∈X справедлива оценка ||Ax||≤M||x||, где M - постоянная. Точная нижняя грань всех таких констант M называется нормой ||A|| оператора A.

(Комментарий. По определению, ∀x∈X ||Ax||≤||A||*||x||, то есть ||A||, во-первых,- одна из верхних граней, а во-вторых ∀ε > 0∃ x_ε∈X: ||Ax_ε||>(||A||-ε)||x_ε||, что означает несдвигаемость верхней грани.

Легко показать, что 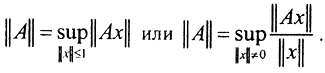У непрерывного оператора можно посчитать конечное значение норм входного и выходного элементов, максимальное значение этого отношения на всем множестве определения дает согласованную норму самого этого оператора. Грубо говоря, это максимальный "коэффициент усиления" преобразования. Поскольку есть норма, то есть число, то множество операторов должно быть замкнуто относительно обычных алгебраических операций. Но будет ли оно пространством, то есть можно ли на этом множестве определить операцию предельного перехода и если да, то будет ли это пространство полным?)

Обозначим множество всех непрерывных линейных операторов, действующих из пространства X в пространство Y, через L(X,Y). Очевидно, L(X,Y) - линейное пространство.

Теорема 1. Пространство L(X,Y) есть нормированное пространство.

□. Достаточно проверить для 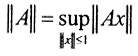аксиомы нормы.

Определение 2. Последовательность линейных непрерывных операторов {A_n}∈ L(X,Y) сходится равномерно к оператору A∈ L(X,Y), если ∀ε > 0∃ N=N(ε)> 0: ∀n>N, ∀x из шара 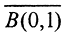||A_nx-Ax||<ε.

Это обозначают как ||A_n-A|||_n→∞→ 0.

Теорема 2. Если X есть нормированное пространство, a Y банахово, то пространство L(X,Y) банахово в смысле равномерной сходимости.

□. Надо показать, что существует непрерывный линейный оператор A, который является пределом равномерно сходящейся последовательности операторов A_n.

1. Покажем существование непрерывного оператора 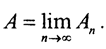∈ L(X,Y). Рассмотрим произвольную фундаментальную последовательность {A_n}∈ L(X,Y). Для любого элемента x∈X последовательность {A_nx} фундаментальна, так как 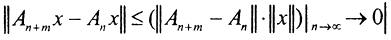и m > 0. Пространство Y банахово, то есть найдётся 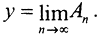Таким образом, каждому элементу x∈X мы поставили в соответствие единственный элемент 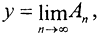y∈Y. Оператор A линеен, так как линейны операторы A_n.

2. Покажем, что оператор A непрерывен и является пределом для последовательности операторов A_n. В самом деле, так как последовательность {A_n} фундаментальна в L(X,Y), то последовательность норм {||A_n||} ограничена, то есть ||A_n||≤m. С другой стороны, 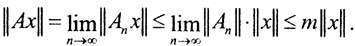Таким образом, ||A||≤m, и, следовательно, оператор A является непрерывным. В силу фундаментальности последовательности операторов A_n, ∀ε > 0∃ N=N(ε)> 0: 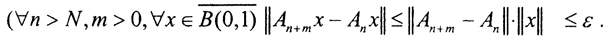Перейдем в данном неравенстве к пределу при m→∞. Тогда ∀ε > 0∃ N=N(ε)> 0: ∀n>N при условии ||x||≤1 выполнится ||Ax-A_nx||≤ε. Это значит, что 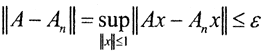при всех n>0, то есть □

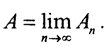(Комментарий. В пространстве линейных непрерывных операторов существуют и другие типы сходимости. Рассмотрим последовательность операторов ортогонального проецирования в гильбертовом пространстве. Пусть 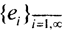есть некоторый ортонормированный базис в гильбертовом пространстве l₂: e₁={1,0,0,...}, e₂={0,1,0,...},... и так далее. Тогда произвольный элемент x∈X ⊂ l₂ представим в виде ряда Фурье 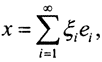где ξ_i=(x,e_i). 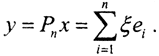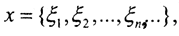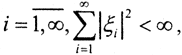Определим оператор проецирования P_n на подпространство l₂, натянутое на первые n элементов базиса, как Тогда а P_nx={η₁,η₂,...,η_n}. То есть η_i=0, i> n . Тогда 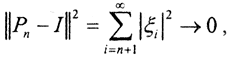как остаток сходящегося ряда, где I - тождественный оператор. То есть P_n→I, но это какая-то другая сходимость, потому что равномерной сходимости нет. В самом деле, как только n> N, то ||P_nx-Ix||< ε для любого x. Пусть x=e_n+1. Тогда ||P_ne_n+1-P_n+pe_n+1||=||e_n+1||=1, так как P_n не сохраняет e_n+1, а P_n+p сохраняет. Это рассуждение подводит нас к следующему определению.)

Определение 3. Последовательность операторов {A_n}∈ L(X,Y) называется поточечно (сильно) сходящейся к оператору A∈ L(X,Y), если ∀ x∈X ||A_nx-Ax|||_n→∞→0.

(Комментарий. Поточечная сходимость означает сходимость в каждой точке пространства. Мы показали, что поточечная (сильная) сходимость последовательности операторов не влечет за собой, вообще говоря, равномерной сходимости этих же операторов. Обратное всегда верно: равномерная сходимость последовательности операторов всегда влечет за собой поточечную. Действительно, ||A_nx-Ax|||_n→∞ ≤ (||A_n-A||*||x||)|_n→∞→0.)

Будет ли пространство L(X,Y) банаховым в смысле поточечной сходимости? Из принципа равномерной непрерывности Банаха Штейнгауса следует, что если X и Y банаховы пространства, то пространство L(X,Y) банахово в смысле поточечной сходимости.