
2. Пространства носителей
(Комментарий. Стандартные пространства - это метрические или нормированные пространства со стандартными носителями и со стандартными метриками или нормами.
Стандартные носители
- кортежи
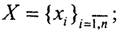
- ограниченные последовательности
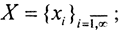
- множество непрерывных или непрерывно дифференцируемых функций f(x) на сегменте [a,b].
)
Стандартные метрики (нормы)
1. Гёльдеровские (радикальные) метрики: 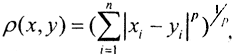 или
или 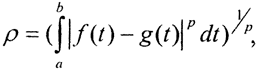 или
или 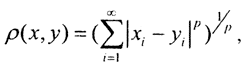 p∈[1,∞). При p=2 эти метрики иногда называют энергетическими, так как в прикладных задачах они связана с энергией.
p∈[1,∞). При p=2 эти метрики иногда называют энергетическими, так как в прикладных задачах они связана с энергией.
2. Чебышевские (супремальные), или равномерные, метрики: 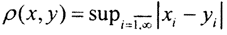 или
или 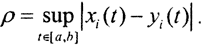 .
.
Определение. Множество Х называется нормированным пространством, если: X - линейное пространство над полем действительных или комплексных чисел и для каждого элемента x∈X определено вещественное число, называемое его нормой и обозначаемое ||x||,по следующим правилам:
а) ||x||≥0 для любого x ∈ L: ||x||=0 ⇔ x=0;
б) ||λx||=|λ|||x|| для любого x ∈ L и любого λ;
в) ||x+y||≤||x||+||y|| для любых x,y ∈ L
Расстояние в нормированном пространстве X определим так: ∀ x,y ∈ X: ρ(x,y)=||x-y||. Тогда при y=0 метрики становятся нормами, то есть норма элемента ||x|| - это расстояние между элементом x и нулевым элементом. Нормированное пространство всегда метрическое с метрикой ρ(x,y)=||x-y|| ∀ x,y ∈ X. Обратное, вообще говоря, неверно, то есть не любая метрика может быть нормой.
Пример. Метрика ρ|arctgλx| не может быть нормой, т.к. |arctgλx|≠λ|arctgx|.
Пример. Рассмотрим пространство R2p.
При p=1 норма элемента ||x||1 = |x|+|y| называется октаэдрической, потому что единичной сферой в трёхмерном случае ||x||1=|x|+|y|+|z|=1 будет октаэдр.
При p=2 норма элемента ||x||2 = (|x|2+|y|2)1/2 - евклидова (сферическая) норма, потому что единичной сферой в трёхмерном случае будет обычная сфера.
Чебышёвская (кубическая) норма: ||x||∞=max{|x|,|y|}, потому что единичной сферой в трёхмерном случае ||x||∞=max{|x|,|y|,|z|}=1 будет куб.
При p→ ∞ гёльдеровская группа норм стремится к чебышевской.
Стандартные метрические (нормированные) пространства
1. Rnp - n-мерное арифметическое пространство с радикальной метрикой (при p=2 это эвклидово пространство).
2. Rn - n-мерное арифметическое пространство с супремальной метрикой.
3. lp пространство ограниченных последовательностей с радикальной метрикой (координатное гильбертово пространство) (при p=2 это такие последовательности, сумма квадратов элементов которых конечна (т.е. ряд сходится). Эту сумму квадратов, т.е. сумму ряда, назовем квадратом длины вектора. Операции сложения и умножения на число определим как для конечномерных векторов-столбцов, то есть поэлементно.)
4. l∞ или l пространство ограниченных последовательностей с супремальной метрикой.
5. Cp[a,b] - пространство непрерывных функций с радикальной метрикой. Его пополнение Lp[a,b] - лебегово пространство. Норма пространства Лебега 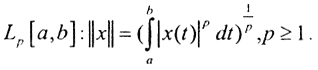 При p=2 пространство Lp[a,b] гильбертово и обозначается как H2.
При p=2 пространство Lp[a,b] гильбертово и обозначается как H2.
6. C[a,b] - пространство непрерывных функций с супремальной метрикой (чебышевское).
7. Cn[a,b] или C(n)[a,b] - пространство n раз непрерывно дифференцируемых функций с супремальной нормой (такая норма называется дифференциальной): 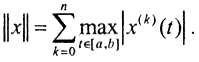
8. Cnp[a,b] - пространства непрерывно дифференцируемых функций с радикальной метрикой. Их пополнение Wnp[a,b] - пространства Соболева. Норма пространств Соболева 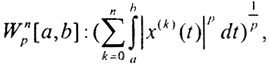 p≥ 1. При p=2 пространство Wn2[a,b] гильбертово и обозначается как Hn.
p≥ 1. При p=2 пространство Wn2[a,b] гильбертово и обозначается как Hn.
Определение 1. Полное линейное нормированное пространство называется банаховым пространством или B- пространством.
Определение 2. Банахово пространство, в котором норма вводится через скалярное произведение, называется гильбертовым или H-пространством. Другими словами, гильбертовым называется полное бесконечномерное евклидово пространство.
Определение 3. Последовательность {xn} точек xn линейного нормированного пространства L сходится к точке x (сходится по норме), если ||xn-x|||n→∞ → 0 или ∀ε > 0 ∃ N=N(ε):(n>N⇒ ||xn-x||<ε).
Обозначение используется обычное: {xn}→x.
Сходимость по норме пространства C[a,b] называется равномерной сходимостью. Сходимость по норме пространства L2[a,b] называется сходимостью в среднем.
Определение 4. Метрика (норма) p1 сильнее, чем метрика (норма) p2, если из сходимости по p1 следует сходимость по p2, но существует хоть одна последовательность, которая сходится по норме p2, но не сходится по норме p1.
(Комментарий. B конечномерных пространствах все метрики (нормы) топологически эквивалентны в следующем смысле: для шара B(x0,R) радиуса R, построенного на основе одной из норм, можно построить вписанный в него и описанный вокруг него шары, построенные на основе другой нормы (разумеется, другого радиуса). Поэтому здесь причиной некорректности может быть только вырожденность оператора A, т.е. оператор A должен быть проектором. Другими словами, размерности конечномерных пространств X и Y не совпадают. Это и приводит к информационной недоопределённости, то есть некорректности прямой или обратной задачи.
В бесконечномерных пространствах это не так. Покажем, что чебышевская норма, по крайней мере, не слабее гёльдеровской, а дифференциальная не слабее чебышевской.
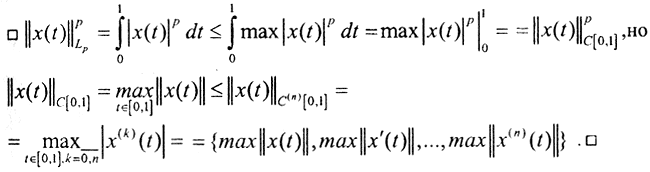
Это и даёт теоретическую возможность подбора пространств для того, чтобы задача стала корректной. Кроме того, в бесконечномерных пространствах по теореме Рисса Фишера все сепарабельные гильбертовы пространства изометрически изоморфны, т.е. тоже фактически эквивалентны. Сепарабельность означает, что на абстрактном множестве есть всюду плотное счётное множество ("счётный скелет"), то есть в бесконечномерном пространстве можно построить счетный базис. Мощности любых двух полных ортонормированных систем в сепарабельном пространстве одинаковы. В произвольных банаховых пространствах такой эквивалентности нет. По теореме Йордана фон Неймана, если ∀f,g ∈ B, где B - банахово пространство, и для этих элементов выполняется правило параллелограмма ||f+g||2+||f-g||2=2(||f||2+||g||2), то можно определить скалярное произведение так, что пространство B станет гильбертовым пространством. Для многих банаховых пространств это не так. Например, пространство функционалов L[R], таких, что 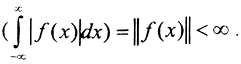 Если f(x) и g(x) - непрерывные функции с непересекающимися носителями, то
Если f(x) и g(x) - непрерывные функции с непересекающимися носителями, то 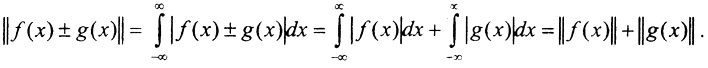 Таким образом, правило параллелограмма не выполняется, так как ||f+g||2+||f-g||2=2(||f(x)||+||g(x)||)2. (Вообще, скалярное произведение для радикальной нормы Lp можно определить только при p=2) Поэтому в произвольных В-пространствах задача может быть корректной или нет в зависимости от выбора норм.)
Таким образом, правило параллелограмма не выполняется, так как ||f+g||2+||f-g||2=2(||f(x)||+||g(x)||)2. (Вообще, скалярное произведение для радикальной нормы Lp можно определить только при p=2) Поэтому в произвольных В-пространствах задача может быть корректной или нет в зависимости от выбора норм.)
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'