
1. Выбор пространств
Мы рассматриваем операторное уравнение общего вида Ax=y, где A - линейный оператор, действующий из, вообще говоря, топологического пространства X в топологическое пространство Y. В реальной задаче выбор передающего и принимающего пространств достаточно серьезная проблема. С одной стороны, ими определяются свойства оператора A, а с другой стороны, выбор пары пространств не произволен, а определяется как физической моделью, так и возможностями измерений в конкретных экспериментах.
(Комментарий. В произвольных банаховых пространствах задача может быть корректной или нет в зависимости от выбора топологий. Обычно используют топологии нормированных пространств L2, C, Cn, Wnp.
Пример 1. Волновое уравнение можно представить в таком виде: 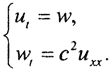 Выберем банахово пространство с нормой ||u||=max{|u|,|w|}. Легко проверить, что решение волнового уравнения будет иметь вид u(x,t)=coskx*cosckt.
Выберем банахово пространство с нормой ||u||=max{|u|,|w|}. Легко проверить, что решение волнового уравнения будет иметь вид u(x,t)=coskx*cosckt.
Тогда 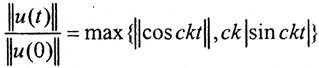 и для любого t> 0 может быть сколь угодно большим. Это некорректная задача. Однако такое решение не имеет физического смысла, так как размерности u и w разные [18].
и для любого t> 0 может быть сколь угодно большим. Это некорректная задача. Однако такое решение не имеет физического смысла, так как размерности u и w разные [18].
Пример 2. Пусть A - непрерывный линейный оператор и существует A-1, то есть решение единственно. Определим в пространстве Y норму элемента y как ||y||=||A-1y||. Тогда 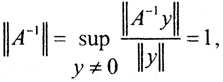 следовательно, оператор A-1 непрерывен и задача корректна.)
следовательно, оператор A-1 непрерывен и задача корректна.)
Казалось бы, достаточно подобрать соответствующую пару топологических пространств X и Y так, что топология пространства Y будет сильнее, чем топология пространства X, и обратная задача Ax=y для этой пары пространств будет корректной. Действительно, в задаче Коши для уравнения Лапласа, в задаче Коши для уравнения теплопроводности с обратным временем, а также во многих других задачах подобного типа подобрать пары пространств, в которых задачи станут корректными, сравнительно нетрудно.
Однако такой подход к некорректным задачам оставляет в стороне очень важный с точки зрения приложений аспект. Дело в том, что если уравнение Ax=y рассматривается в связи с математическим моделированием реального физического явления, то правую часть уравнения часто получают на основании показаний физических приборов. Поскольку приборы обладают погрешностями, мы не можем в таких случаях считать правую часть этого уравнения заданной абсолютно точно. Мы можем считать лишь, что нам задан элемент yδ, удовлетворяющий неравенству ||y-yδ||≤ δ, где число определяется точностью приборов. При этом норма пространства, в котором нам известна оценка погрешности правой части, не может задаваться произвольно, она диктуется постановкой системы измерений. Как правило, это или норма в пространстве C, то есть нам известна оценка максимальной погрешности измерений, или норма в пространстве L2, то есть известна оценка средней квадратичной погрешности.
Возможна, хотя и представляет дополнительные технические трудности, постановка системы измерений, когда погрешность мала вместе со своей производной, то есть норма задаётся в пространстве C1 или W12. Уже здесь оценить погрешность δ, если f(y)∈C1[a,b], практически невозможно, так как в этом случае 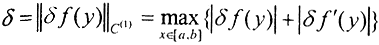 и требует измерения величины производной. Постановка же измерений, когда погрешность мала вместе со второй производной (пространства C2, W22), уже мало реальна.
и требует измерения величины производной. Постановка же измерений, когда погрешность мала вместе со второй производной (пространства C2, W22), уже мало реальна.
Обычно работают в пространстве Чебышёва C[a,b], где погрешность измерения правой части 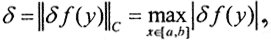 или в пространстве Лебега L2[a,b], где погрешность измерения правой части
или в пространстве Лебега L2[a,b], где погрешность измерения правой части 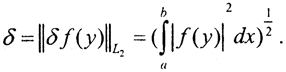 Поэтому, например, интегральное уравнение Вольтерра I рода, некорректное на паре пространств (C,C1) всё равно нельзя решать на паре пространств (C,C), где задача его решения корректна. Кроме того, есть уравнения, задача решения которых некорректна в любой разумной паре пространств (это, например, уравнения Фредгольма I рода). Задача решения операторного уравнения первого рода не может быть корректной, так как оператор, обратный вполне непрерывному оператору в бесконечномерном пространстве, не является непрерывным. Мы это позже покажем.
Поэтому, например, интегральное уравнение Вольтерра I рода, некорректное на паре пространств (C,C1) всё равно нельзя решать на паре пространств (C,C), где задача его решения корректна. Кроме того, есть уравнения, задача решения которых некорректна в любой разумной паре пространств (это, например, уравнения Фредгольма I рода). Задача решения операторного уравнения первого рода не может быть корректной, так как оператор, обратный вполне непрерывному оператору в бесконечномерном пространстве, не является непрерывным. Мы это позже покажем.
Напомним некоторые факты из теории пространств.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'