7. Уравнения Навье Стокса

(Комментарий. В августе 1900 года на международном математическом конгрессе в Париже математик Дэвид Гилберт изложил список проблем, которые, как он полагал, предстояло решить в ХХ веке. В списке было 23 пункта, в том числе и проблема решения уравнений Навье Стокса. По примеру Гилберта в мае 2000 года Математический институт Клэя в США назвал семь проблем XXI века. Решение уравнений Навье Стокса (1822 год) в общем виде - одна из них.)

Уравнения Навье-Стокса - это уравнения движения вязкой жидкости. Они представляют собой законы сохранения импульса и массы плюс уравнения состояния, связывающие давление p, плотность ρ и закон сохранения энергии.

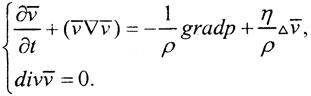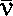В простейшем случае они имеют вид: Здесь - скорость; η - кинематическая вязкость; ρ - плотность, а 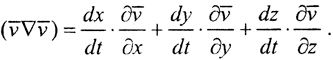Для уравнений Навье-Стокса:

- доказано существование и единственность решения только для плоского и осесимметричного ламинарного течения (при ограниченном и достаточно малом времени t).

- доказано существование, но не доказана единственность решения для пространственных ламинарных течений при малых энергиях и малом времени t и для обтекания препятствий произвольной формы в стационарных потоках двух и трёх измерений.

- при числах Рейнольдса 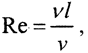находящихся в пределах 1600-2000 в реальности возникает турбулентный режим, а в теории этого нет. При турбулентном режиме существует исключительная чувствительность к изменению коэффициентов уравнения: при изменении числа на 0,05 % решения совершенно отличаются друг от друга, а это признак некорректности.

- Хопф (1952г) доказал некорректность задачи Коши для уравнений Навье-Стокса, если скорость течения растёт линейно, а давление - квадратично.

Максимально упрощённое галёркинское приближение уравнений Навье Стокса, записанных для задачи Бенара и имеет вид: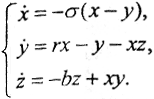 Это система уравнений Лоренца, демонстрирующая стохастическое поведение решения, то есть некорректность в большом. Существуют обоснованные предположения, что динамическая неустойчивость системы уравнений Лоренца связана с проблемой турбулентности и другими проблемами неустойчивых течений в гидро и аэродинамике.