6. Дифференцирование функции, известной приближенно

Это, наверное, самая старая и известная задача. Если рассматривать исходные данные x₁(t) и решение 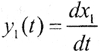как элементы пространства C[a,b], а функция x₁(t) непрерывно дифференцируема, то, положив x₂(t)=x₁(t)+Asinωt и 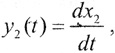получим, что ||x₁-x₂|||_C=max|Asinωt|=|A|, t ∈ [a,b]. И даже если A ≠0 очень мало, величина ||y₁-e₂|||_C=max|Aωcosωt|=|Aω|, t ∈ [a,b] может быть сделана сколь угодно большой за счет выбора ω. То есть это некорректная задача. Идея её решения появилась до метода регуляризации и хорошо его иллюстрирует.

Рассмотрим семейство операторов 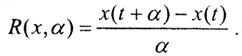Пусть функция x(t) непрерывно дифференцируема и δ - точность исходных данных. Таким образом, имеется приближенное значение исходной функции x_δ(t)=x(t)+v(t), причём при всех t ∈ [a,b] выполнено неравенство |v(t)|≤δ. Тогда 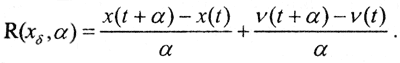При α→0 первое слагаемое стремится к производной 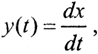а второе слагаемое при всех t ∈ [t,t+α] не превосходит 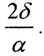Если взять, например, α=√δ, то при δ→0 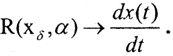Таким образом, при замене производной разностным отношением приращения аргумента должны быть не слишком малыми по сравнению с погрешностью значений функции, но и не слишком большими, при которых задача теряет смысл. Это и есть регуляризация и её главная проблема: выбор параметра регуляризации.