8. Конечномерные динамические системы

Динамическая система (ДС) - модель какого-либо процесса или явления во времени, в которой чётко определено состояние системы в данный момент времени и законы эволюции.

(Комментарий. В основу теории динамических систем положены два понятия: понятие состояния (информация о системе в какой-то (начальный) момент времени и понятие оператора эволюции или динамики (правила, описывающего эволюцию системы во времени). Эволюцию можно наблюдать в пространстве состояний, или фазовом пространстве, абстрактном пространстве, в котором координатами служат компоненты состояния. При этом координаты выбираются в зависимости от контекста. В случае механической системы это могут быть положение и скорость, в случае экологической модели - объём популяций различных биологических видов. Простейшие ДС - система обыкновенных дифференциальных уравнений x_S=f_S(x₁,...,x_S,t) или уравнений в частных производных. Фазовое пространство конечномерных автономных (то есть систем, не содержащих в явном виде временной параметр t) динамических систем- n-мерное евклидово пространство начальных условий, а состояние системы определяется изображающей точкой в фазовом пространстве.)

Для конечномерных динамических систем имеют место теоремы существования, единственности и непрерывной зависимости решения задачи Коши от параметров и начальных условий, которые сформулированы (при некоторых достаточных условиях) для невырожденных систем обыкновенных дифференциальных уравнений, записанных в нормальной форме. То есть некорректность здесь полностью исключена. Однако если условия этих теорем не выполняются, то даже линейная система обыкновенных дифференциальных уравнений может стать некорректной. Рассмотрим линейную систему 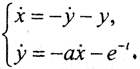Нормальная форма Коши для неё имеет вид 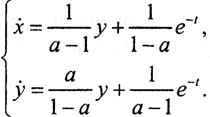Ясно, что при a=1 система становится вырожденной и непрерывная зависимость решения от параметра исчезает. Это значит, что её нет и в исходной системе. А это уже некорректность.

Это случай аналогичен тому, что происходит в системах линейных алгебраических уравнений и будет подробно рассмотрен ниже.

Но даже если условия этих теорем выполнены, в нелинейных конечномерных динамических системах, фазовое пространство которых имеет порядок три и выше может возникнуть ситуация, которая называется "некорректностью в большом".

Обычно считается, что фазовое пространство подчинено аксиоме Хаусдорфа (аксиома отделимости): для любых двух точек x₁ и x₂ метрического пространства X существуют открытые шары B(x₁,ε) и B(x₂,ε) и такое ε>0, для которого их пересечение пусто. На самом деле, так как начальные условия нельзя задать в точке, всегда существует такое ε>0, что в шаре B(x₀,ε) все точки неразличимы. Именно этот шар движется в фазовом пространстве. Траектория его в фазовом пространстве называется инвариантной (состоящей из траекторий) хаусдорфовой трубкой. Фазовые траектории в фазовом пространстве динамических систем не пересекаются в силу принципа детерминизма и, следовательно, теоремы существования и единственности решения дифференциальных уравнений, но трубки могут пересекаться.

(Комментарий. Это значит, что даже в простых конечномерных фазовых пространствах с сохраняющимся или сжимающимся фазовым объемом возможно очень сложное движение. Оно возникает, если фазовые траектории нелинейной системы неустойчивы, то есть трубка расширяется и в условиях замкнутого и ограниченного фазового объема "размазывается" по всему фазовому пространству. В линейном случае это невозможно. В нелинейном случае, если эвклидова размерность фазового пространства не меньше трёх, возникает явление стохастичности динамических систем: в фазовом пространстве системы существуют неустойчивые направления, по которым они фазовые траектории разбегаются, и существуют устойчивые, по которым сбегаются.)

Фазовые траектории не могут быть неустойчивыми одновременно по всем направлениям это приведет к неограниченности фазового объема, в котором неустойчивые траектории располагаются; поэтому такие траектории могут быть только седловыми они неустойчивы по одним направлениям и устойчивы по другим. Эти направления не должны пересекаться, что порождает очень сложную систему траекторий (гомоклиническую структуру) и полную независимость, начиная с некоторого момента времени, от начальных условий. Поскольку существуют устойчивые траектории и фазовый объём ограничен, то это, всё-таки, притягивающее множество, то есть аттрактор. Такие аттракторы называются странными. Популярнейшим примером конечномерных динамических систем, в фазовом пространстве которых при некоторых значениях параметров возникает странный аттрактор, является система уравнений Лоренца, демонстрирующая стохастическое поведение. Решение дифференциального уравнения со странным аттрактором в фазовом пространстве выглядит как белый шум (случайный процесс).

Пример. Рассмотрим пример задачи, некорректной в большом, на языке отображений. В фазовом пространстве расположим плоскость, которая называется бесконтактной или плоскостью Пуанкаре, т.е. такую, которую фазовая траектория пересекает не касаясь. Пусть n - предыдущее пересечение, а n+1 - последующее. Обозначим через x_i координату точки пересечения в некоторой удобной системе координат. Тогда x_i+1=f(x_i) есть отображение точки x_i, соответствующее данной динамической системе. 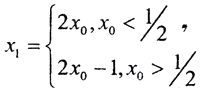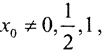Если система третьего порядка, x₀ - начальное состояние, а и то такое отображение называется "отображением пекаря". Отображение пекаря моделирует трёхмерную динамическую систему с неустойчивыми фазовыми траекториями в замкнутом ограниченном фазовом пространстве. В реальности отображение пекаря в чистом виде не существует, но основные его свойства характерны для любой некорректной в большом задачи. Запишем x₀ в виде: 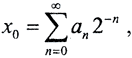причём 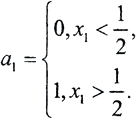Каждая новая итерация будет приводить к сдвигу Бернулли: x₀=0,a₁a₂...a_i...; x₁=0,a₂a₃...a_i+1...

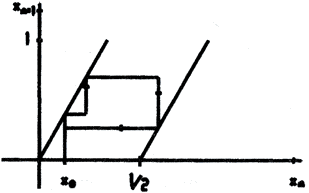
Свойства отображения пекаря:

1. Это, очевидно, растягивающее отображение в ограниченном фазовом объеме - единичном квадрате.

2. Неустойчивость к начальным условиям. Здесь есть резкое разбегание близких траекторий: если первоначальная разница между точками была в k-м знаке после запятой, то, спустя итераций разница между ними будет в 1-м знаке, а после k+1 итераций будет потеряна вся информация о начальных данных. Решение теперь от них не зависит и их невозможно восстановить. Эта необратимость по отношению к причинно-следственным или каузальным связям тоже характерная черта некорректности.

3. Бернуллиевость. Мы имеем дело с чисто случайным процессом, как в схеме испытаний Бернулли.

4. Эргодичность. Пусть точка x₀ задана приближённо, то есть с конечным числом знаков после запятой: x₀=0,a₁a₂...a_i+ε,a_n={0,1}. Число комбинаций из n элементов равно 2ⁿ, то есть конечно, а на самом деле x₀=0,a₁a₂...a_i..., то есть имеет бесконечное число знаков после запятой. Тогда, в соответствии с принципом Вейерштрасса, ∀ ε>0 изображающая точка сколь угодно близко подойдет к любому своему положению, в том числе и начальному, причём бесконечное число раз. Это и есть свойство эргодичности.

Были приведены, как мне кажется, самые яркие примеры некорректных задач, спектр которых, на самом деле, значительно шире [1-10, 12-15, 19,20,22].