3. Задача Дирихле для волнового уравнения

В одномерном случае она имеет вид

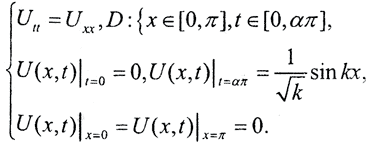
Ясно, что задача переопределена.

В соответствии с методом Фурье полагаем U=TX.Тогда уравнение примет вид: T^''X=X^''T. Разделяя переменные 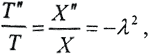получаем систему уравнений: 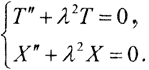Второе уравнение имеет решение: X=C₁sinλx+C₂cosλx. Исходя из первого граничного условия, получаем, что C₂ = 0. Тогда: C₁sinλπ=0 ⇒ λπ=πk ⇒λ=k ⇒ X=C₁sinkx. Аналогично находим решение первого уравнения системы: T=C₂sinkt. 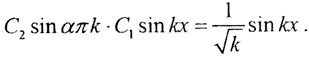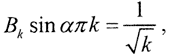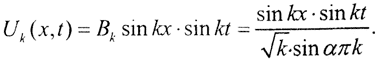Исходя из второго граничного условия, получаем: Пусть B_k=C₁C₂, то есть тогда Ясно, что решение не имеет смысла, то есть задача некорректна, когда sinαπk=0, то есть απk=nk, или 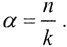Таким образом, при любом целом или рациональном числе α задача не имеет смысла. Так как |sin(απk-πn)|=|sin(απk)cos(πn)-sin(πn)cos(απk)|=|sin(απk)|, покажем, что если α иррационально, то для любого ε> 0∃n, k∈ N, такие, что |αn-k|< ε. Разобьем промежуток [0,1) на N частей так, чтобы 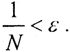Рассмотрим дробную часть: 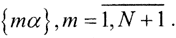Так как этих точек на одну больше, чем количество наших интегралов, существует две точки {αp} и {αq}, принадлежащие одному интервалу (принцип Дирихле), где p>q - натуральные числа. Это означает, что (p-q)α отличаются от некоторого целого n меньше, чем на 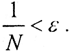Пусть k=p-q. Тогда |nα-k|< ε, то есть при α∋ I знаменатель в ноль не обратится, но сколь угодно близко и нерегулярно к нему подойдет. Отсюда следует, что решение неустойчиво и при n→∞ сколь угодно малое отклонение от начальных данных приводит к сколь угодно большому изменению решения.

(Комментарий. Аналогично: если прямая, проходящая через начало координат по равномерной сетке, имеет иррациональный угловой коэффициент, то она бесконечно близко будет подходить к бесконечному числу узлов, но никогда не пересечет ни один узел; при этом нельзя указать правило, по которому прямая будет приближаться к узлам.)