2. Классическая задача Адамара

(Комментарий. Сформулировав понятие корректности, Адамар привел пример дифференциального уравнения, которое, по его мнению, не соответствовало никакой реальной физической задаче. Это задача Коши для уравнения Лапласа. Позже обнаружили связь между задачей, эквивалентной задаче Коши для уравнения Лапласа, и некоторыми вопросами гравитационных и магнитных аномалий. Это задача измерения напряжённости гравитационного поля плоской Земли, с неровностями, осадками и уплотнениями, расстояние между которыми меньше толщины слоя осадков.

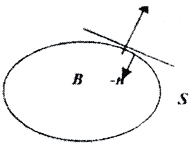
Требуется перерасчёт поля вниз, в недоступную область. Компоненты напряжённости поля удовлетворяют уравнению Лапласа Δu=0, u|_r→∞→0. Для уравнения Лаласа существуют три классические краевые задачи, которые формулируется так: найти решение уравнения Лапласа внутри области B, ограниченной замкнутой поверхностью s, если на поверхности s выполняются граничные условие или первого рода: u(x,y,z)|_s=u₀(x₀,y₀,z₀), или второго рода: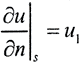 (Очевидно, что стационарный поток устанавливается, когда суммарный поток через границу равен нулю, то есть требуется ещё одно условие: 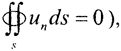или граничное условие третьего рода: 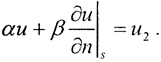Ясно, что u₀, u₁, u₂ - известные функции, а α и β - известные константы.)

Однако для задачи Адамара эти классические постановки не подходят, так как невозможно задать или измерить поле внизу, в недоступной области. Поэтому здесь естественна задача Коши, неестественная, некорректная по постановке для эллиптических задач. В двумерном случае задача имеет вид:

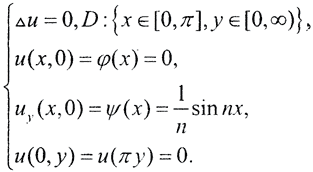
Получим её решение методом Фурье.

Пусть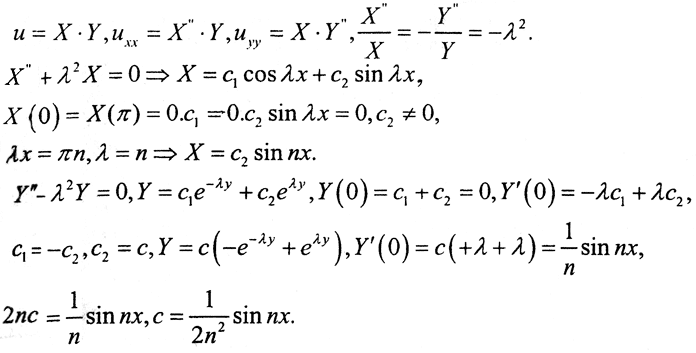

Тогда решение этой задачи имеет вид 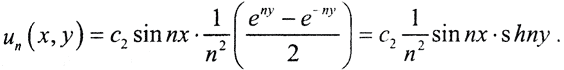Норма этого решения в пространстве C[a,b], в котором реально и проводятся измерения, 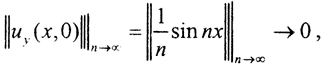причём чем меньше отклонение от нуля начальных данных, тем больше отклонение решения.