
1. Постановка задачи измерения
Обычно в общей постановке задачи анализа эксперимента мы имеем нелинейное интегральное уравнение 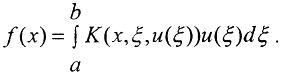 Здесь f(x) и u(ξ) - измеренная и искомая функции соответственно, а ядро интегрального уравнения K(x,ξ,u(ξ)) зависит от искомой функции. Интегральные уравнения появляются при рассмотрении обратных задач, возникающих в том числе и в тех случаях, когда непосредственное измерение физических характеристик невозможно или затруднительно. Потом оно линеаризируется, так как большинство методов исследования применимо лишь к линейным задачам. В нашем случае получаем линейное интегральное уравнение, сопоставляющее функцию u(x) с новой функцией Au=f(x), определяемой с помощью формулы
Здесь f(x) и u(ξ) - измеренная и искомая функции соответственно, а ядро интегрального уравнения K(x,ξ,u(ξ)) зависит от искомой функции. Интегральные уравнения появляются при рассмотрении обратных задач, возникающих в том числе и в тех случаях, когда непосредственное измерение физических характеристик невозможно или затруднительно. Потом оно линеаризируется, так как большинство методов исследования применимо лишь к линейным задачам. В нашем случае получаем линейное интегральное уравнение, сопоставляющее функцию u(x) с новой функцией Au=f(x), определяемой с помощью формулы 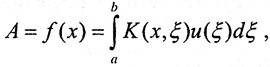 где K(x,ξ) - некоторая фиксированная непрерывная функция двух переменных. Везде далее будем полагать, что ядро K(x,ξ) непрерывно по совокупности аргументов или удовлетворяет условию Гильберта Шмидта:
где K(x,ξ) - некоторая фиксированная непрерывная функция двух переменных. Везде далее будем полагать, что ядро K(x,ξ) непрерывно по совокупности аргументов или удовлетворяет условию Гильберта Шмидта: 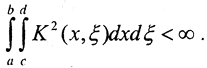 Поскольку это уравнение чаще всего решать ещё нельзя, проводится алгебраизация задачи, то есть сведение её к СЛАУ
Поскольку это уравнение чаще всего решать ещё нельзя, проводится алгебраизация задачи, то есть сведение её к СЛАУ 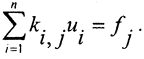 Здесь ui, fi - линейные функционалы от функций u(x) и f(x), то есть или их значения в опорных точках, или коэффициенты разложения по какой- либо ПОНС (см. разд. 1 главы VII).
Здесь ui, fi - линейные функционалы от функций u(x) и f(x), то есть или их значения в опорных точках, или коэффициенты разложения по какой- либо ПОНС (см. разд. 1 главы VII).
Пример. Задача об измерении распределения яркости света.
Изображение и объект геометрически подобны, поэтому схема измерения яркости изображения с помощью прибора выглядит так. Выберем масштабы вдоль осей x и ξ так, чтобы для любых двух взаимно соответствующих точек x и ξ выполнялось условие x=ξ, где ξ - светящаяся точка объекта, а x - точка изображения. Это называется калибровкой прибора.
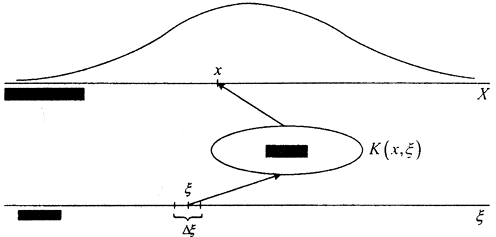
Постановка задачи измерения
Светящаяся точка ξ объекта влияет на освещённость всего изображения, причём наибольшая яркость приходится на точку ч. Пусть u(ξ) - плотность яркости объекта, тогда u(ξ)Δξ - яркость элемента Δξ, а K(x,ξ)u(ξ)Δξ - яркость изображения в точке x, где K(x,ξ) - аппаратная функция или ядро соответствующего интегрального уравнения. Яркость всего объекта имеет вид 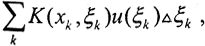 где суммирование проводится по конечной длине объекта l. Переходя к пределу в этой интегральной сумме Римана, получим распределение яркости изображения (плотность яркости)
где суммирование проводится по конечной длине объекта l. Переходя к пределу в этой интегральной сумме Римана, получим распределение яркости изображения (плотность яркости) 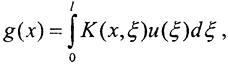 где K(x,ξ) - известная аппаратная функция. Возможны следующие постановки задачи.
где K(x,ξ) - известная аппаратная функция. Возможны следующие постановки задачи.
1. g(x) - распределение плотности яркости изображения известно (измерено), а ищется u(ξ) - распределение плотности яркости объекта. Тогда это уравнение называется интегральным уравнением Фредгольма I рода.
2. Изображение таково, что яркость его пропорциональна яркости объекта u(x)=λg(x), тогда 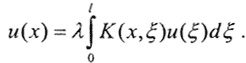 Это уравнение называется однородным интегральным уравнением Фредгольма II рода.
Это уравнение называется однородным интегральным уравнением Фредгольма II рода.
3. Если потребовать, чтобы разность плотностей яркости изображения и объекта была заданной функцией f(x)=u(ξ)-λg(x), то 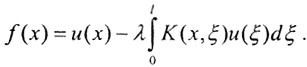 Это уравнение называется неоднородным интегральным уравнением Фредгольма II рода.
Это уравнение называется неоднородным интегральным уравнением Фредгольма II рода.
Ядро K(x,ξ) этого уравнения определено на квадрате x∈[a,b], ξ∈[a,b] и является заданной непрерывной по совокупности аргументов функцией; f(x) - заданная непрерывная функция, u(x) - неизвестная функция, которую полагаем непрерывной. Все функции полагаем действительными. Если ядро K(x,ξ) отлично от нуля только на треугольнике a≤ξ≤x≤b (т. е. K(x,ξ)=0 при x<ξ), то интегральные уравнения Фредгольма переходят в интегральные уравнения Вольтерра. Уравнения Вольтерра - те уравнения, которые описывают направленные процессы. Они выглядят следующим образом: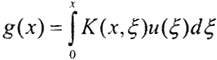 - уравнения Вольтерра I рода,
- уравнения Вольтерра I рода, 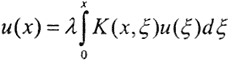 - однородное уравнение Вольтерра II рода,
- однородное уравнение Вольтерра II рода, 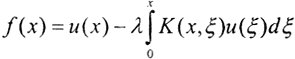 - неоднородное уравнение Вольтерра I рода.
- неоднородное уравнение Вольтерра I рода.
(Комментарий. К интегральным уравнениям сводятся любые задачи математической физики. Даже задачи, записанные в форме уравнений в частных производных, в исходной постановке сформулированы в виде интегральных законов сохранения, то есть интегральных уравнений.
Преимущества интегральных уравнений:
1. Задача решения интегрального уравнения эквивалентна решению задачи Коши для дифференциального уравнения.
2. Одномерную задачу легко сделать n-мерной, положив x={x1,x2,...,xp}. В этом случае появятся многомерные интегралы и этот переход от одной переменной ко многим является естественным. Многомерным аналогом одномерного нелинейного интегрального уравнения 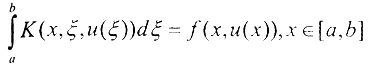 , где ядро K(x,ξ,u(ξ)) и правая часть f(x,u(x)) - заданные функции, является уравнение
, где ядро K(x,ξ,u(ξ)) и правая часть f(x,u(x)) - заданные функции, является уравнение 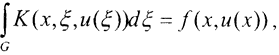 где x={x1,x2,...,xp}, отличающееся от одномерного только тем, что интегрирование проводится по многомерной области G. Поскольку оба уравнения не требуют дополнительных условий и полностью определяют задачу, аналогия является полной. В дифференциальных же уравнениях переход от одной переменной к нескольким, т. е. от обыкновенных дифференциальных уравнений к уравнениям в частных производных, является принципиальным усложнением, приводит к новым постановкам задач и требует новых методов для их обоснования и решения.
где x={x1,x2,...,xp}, отличающееся от одномерного только тем, что интегрирование проводится по многомерной области G. Поскольку оба уравнения не требуют дополнительных условий и полностью определяют задачу, аналогия является полной. В дифференциальных же уравнениях переход от одной переменной к нескольким, т. е. от обыкновенных дифференциальных уравнений к уравнениям в частных производных, является принципиальным усложнением, приводит к новым постановкам задач и требует новых методов для их обоснования и решения.
Корректные задачи сводятся к интегральным уравнениям Фредгольма II рода или сингулярным интегральным уравнениям, которые после некоторых преобразований обычно также сводятся к уравнениям второго рода. Некорректные задачи сводятся к интегральным уравнениям I рода, которые в операторной форме имеют вид Ax=y.)
Покажем некорректность интегрального уравнения Фредгольма I рода. Пусть интегральное уравнение имеет вид 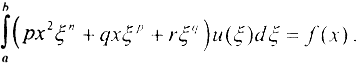 Очевидно, после интегрирования получим f(x)=Ax2+Bx+C. Таким образом, если f(x)=3x2+4x+10-100sin5x, то уравнение с такой правой частью не имеет решений, то есть сколь угодно малое, но конечное изменение правой части делает уравнение неразрешимым и соответственно такая задача является некорректной. Если правая часть - квадратный трёхчлен, то решение есть, но оно не единственно, так как любая интегрируемая на сегменте [a,b] функция u(x) при условиях нормировки
Очевидно, после интегрирования получим f(x)=Ax2+Bx+C. Таким образом, если f(x)=3x2+4x+10-100sin5x, то уравнение с такой правой частью не имеет решений, то есть сколь угодно малое, но конечное изменение правой части делает уравнение неразрешимым и соответственно такая задача является некорректной. Если правая часть - квадратный трёхчлен, то решение есть, но оно не единственно, так как любая интегрируемая на сегменте [a,b] функция u(x) при условиях нормировки 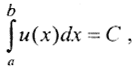
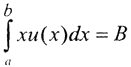 и
и 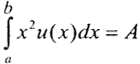 и есть решение интегрального уравнения Фредгольма I рода с этим ядром. Таким образом, интегральное уравнение Фредгольма I рода не всегда имеет решение, а если оно и есть, то оно не единственно. Но даже если решение существует и единственно, оно операторно неустойчиво относительно малых изменений начальных данных, то есть отсутствует непрерывная зависимость решения от правой части уравнения. Покажем это. Пусть
и есть решение интегрального уравнения Фредгольма I рода с этим ядром. Таким образом, интегральное уравнение Фредгольма I рода не всегда имеет решение, а если оно и есть, то оно не единственно. Но даже если решение существует и единственно, оно операторно неустойчиво относительно малых изменений начальных данных, то есть отсутствует непрерывная зависимость решения от правой части уравнения. Покажем это. Пусть 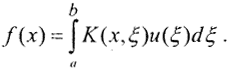 Рассмотрим возмущенное решение u*(x)=u(x)+Asinωx в пространстве L2[a,b], так как конкретные значения ошибок неизвестны и их можно оценить только в среднеквадратичном смысле. Тогда
Рассмотрим возмущенное решение u*(x)=u(x)+Asinωx в пространстве L2[a,b], так как конкретные значения ошибок неизвестны и их можно оценить только в среднеквадратичном смысле. Тогда 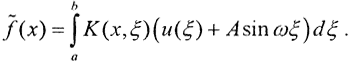 Будем полагать, что ядро K(x,ξ) непрерывно по совокупности аргументов и |K(x,ξ)|≤M, |Kξ(x,ξ)|≤M. Оценим ||δf||=||f*-f||.
Будем полагать, что ядро K(x,ξ) непрерывно по совокупности аргументов и |K(x,ξ)|≤M, |Kξ(x,ξ)|≤M. Оценим ||δf||=||f*-f||.
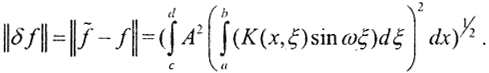
Оценим внутренний интеграл, воспользовавшись интегрированием по частям: 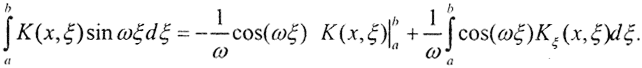
Так как |K(x,ξ)|≤M, |Kξ(x,ξ)|≤M,|cos(ωξ)≤1, то 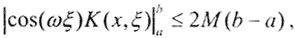 а
а 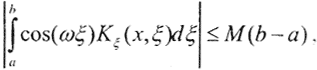 тогда
тогда 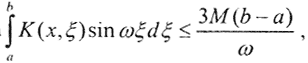 тогда
тогда 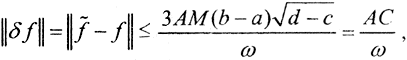 где C - некоторая константа. Это значит, что при достаточно большой круговой частоте ω ошибка измерения может быть сколь угодно малой.
где C - некоторая константа. Это значит, что при достаточно большой круговой частоте ω ошибка измерения может быть сколь угодно малой.
Пространство решений, то есть физических, а следовательно, непрерывных функций, есть пространство Чебышева C[a,b]. Тогда 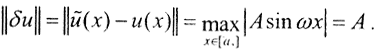 Таким образом, высокочастотное возмущение приведёт к сколь угодно сильному возмущению решения, то есть
Таким образом, высокочастотное возмущение приведёт к сколь угодно сильному возмущению решения, то есть 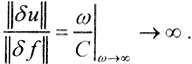 Таким образом, интегральное уравнение Фредгольма I рода не определено ни математически, ни физически.
Таким образом, интегральное уравнение Фредгольма I рода не определено ни математически, ни физически.
(Комментарий. Интегральный оператор Фредгольма есть аналог умножения матрицы K на вектор-столбец u. Это понятно, если умножение матрицы на столбец записать в виде суммы, а для интеграла написать сумму Римана. Тогда интегральные уравнения Фредгольма I рода становятся аналогом системы линейных уравнений. Поэтому главным примером некорректных задач, на котором будет отрабатываться методика их решения, и является система линейных уравнений.
Вид ядра соответствующего уравнения определяется характером задачи. Например, для задачи определения профиля струны, находящейся под действием силы или для задач динамических измерений при приеме любого сигнала ядро имеет вид K(x-ξ). Это ядро типа свертки. Ему соответствует оператор Вольтерра. Собственных значений этот оператор не имеет, поскольку выходной сигнал динамической системы не повторяет входного.)
Пример. Задача динамических измерений.
При выполнении динамических измерений, т.е. измерений, при которых требуется найти не одно простое значение какой-либо физической величины, а зависимость между физическими величинами, возникают аппаратные искажения. Например, зависимость напряжения от времени на выходе некоторого электронного прибора, зависимость интенсивности выходного сигнала на выходе спектрометра от длины волны излучения и т. п. В рамках линейной модели считается, что результат измерения, то есть выходной сигнал φ(τ), является свёрткой входного сигнала f(t) с аппаратной функцией прибора g(t) (импульсным откликом, весовой функцией, функцией Грина).
Аппаратная функция прибора соответствует реакции прибора на поданный на его вход δ(t) - импульс вместо входного сигнала f(t).
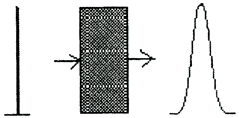
Задача динамических измерений
Тогда уравнение, описывающее эту ситуацию, имеет вид свёртки: 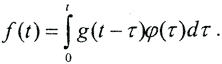 (Свёрткой двух функций φ(t) и g(t) называется функция
(Свёрткой двух функций φ(t) и g(t) называется функция 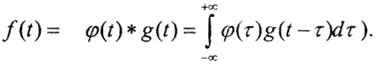 ) Пусть G(ω), Φ(ω), F(ω) есть Фурье-преобразования от функций g(t), φ(τ), f(t), соответственно, то есть
) Пусть G(ω), Φ(ω), F(ω) есть Фурье-преобразования от функций g(t), φ(τ), f(t), соответственно, то есть 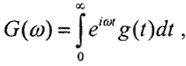
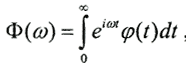
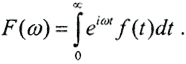 Тогда Фурье-образ результата свертки равен произведению Фурье-образов компонентов свертки: F(ω)=G(ω)*Φ(ω), где под операторами G(ω) и Φ(ω) подразумевается преобразование Фурье. Очевидно, что для нахождения входного сигнала достаточно найти частное Фурье-образов выходного сигнала и аппаратной функции, а потом выполнить обратное преобразование Фурье. Тогда
Тогда Фурье-образ результата свертки равен произведению Фурье-образов компонентов свертки: F(ω)=G(ω)*Φ(ω), где под операторами G(ω) и Φ(ω) подразумевается преобразование Фурье. Очевидно, что для нахождения входного сигнала достаточно найти частное Фурье-образов выходного сигнала и аппаратной функции, а потом выполнить обратное преобразование Фурье. Тогда 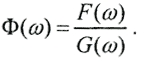 Вернувшись к φ(t), получим
Вернувшись к φ(t), получим 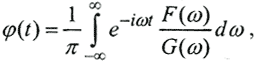 где ω - частота Фурье. При увеличении ω задача становится неустойчивой, так как реальная аппаратная функция прибора g(t-τ) достаточно гладкая, то есть её Фурье-образ G(ω) не содержит высокочастотных составляющих и |G(ω)|||ω|→∞→0. При наличии во входном сигнале шумов (что неизбежно в реальных экспериментах) Фурье-образ выходного сигнала имеет вид
где ω - частота Фурье. При увеличении ω задача становится неустойчивой, так как реальная аппаратная функция прибора g(t-τ) достаточно гладкая, то есть её Фурье-образ G(ω) не содержит высокочастотных составляющих и |G(ω)|||ω|→∞→0. При наличии во входном сигнале шумов (что неизбежно в реальных экспериментах) Фурье-образ выходного сигнала имеет вид 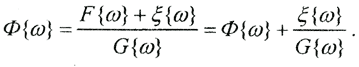 Здесь ξ{ω} Фурье-образ шума ξ(t). Следует отметить, что спектр шумов ξ(t) практически равномерный и, следовательно, ξ{ω} на высоких частотах значительно превышает спектр аппаратной функции G(ω). Это ведет к неограниченному возрастанию второго слагаемого. В результате будет получена лишь быстроосциллирующая функция, не имеющая ничего общего с исходным сигналом. Таким образом, это типичная некорректная задача.
Здесь ξ{ω} Фурье-образ шума ξ(t). Следует отметить, что спектр шумов ξ(t) практически равномерный и, следовательно, ξ{ω} на высоких частотах значительно превышает спектр аппаратной функции G(ω). Это ведет к неограниченному возрастанию второго слагаемого. В результате будет получена лишь быстроосциллирующая функция, не имеющая ничего общего с исходным сигналом. Таким образом, это типичная некорректная задача.
( Комментарий. 1. Очевидным решением этой проблемы является применение фильтра, ограничивающего рассматриваемый спектральный диапазон. Ограничивая спектральный диапазон прибора, мы уменьшаем влияние шумов, но вместе с тем ухудшаем разрешающую способность прибора, что эквивалентно использованию априорной информации о гладкости исходной функции. Это и есть один из основных методов решения некорректных задач регуляризация, параметром которой является полоса пропускания прибора.
2. Наша уверенность в справедливости квантовой механики основана в значительной степени на интерпретации данных экспериментальной спектроскопии атомов и молекул, т.е., по существу, на решении обратной задачи типа 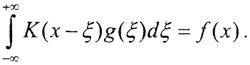 Не означает ли это, что квантовая теория есть просто хорошо продвинутый раздел теории некорректных задач?)
Не означает ли это, что квантовая теория есть просто хорошо продвинутый раздел теории некорректных задач?)
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'