23. Академик Раушенбах: космонавтика - иконография - общая теория перспектив!

Дело не в том, чтобы научиться рисовать, а в том, что бы научиться мыслить.

Стендаль

12 апреля 1961 года. Впервые в истории человечества космический корабль-спутник "Восток" с первым в мире космонавтом на борту Юрием Гагариным за 1 час 48 минут облетел земной шар и благополучно вернулся на Землю. Вслед за тем волны восхищения прокатились по Земле. Земной шар буквально содрогался от этих волн: "Первый полет человека в космос", "Утро космической эры", "Первый гражданин Вселенной",- сообщали газеты, радио, телевидение...

В это же время видавший виды caм лет ИЛ-14 спешил с космодрома Байканур к месту приземления космонавтов! Никто не знал об этом рейсе ИЛ-14, никто не знал имен летевших пассажиров: академиков, профессоров сверхзасекреченных конструкторов. Bi среди них и ведущий специалист в области управления и ориентации космическ аппаратов, доктор технических наук, профессор, впоследствии действительный член Академии наук СССР и Международной академии астронавтики Борис Викторович Раушенбах. На борту "Востока" стояли три дублирующие друг друга системы ориентации, два комплекта органов управления и аппарат ручного управления. Все системы, созданные под руководством Б. В. Раушенбаха, сработали нормально, и их творец был счастлив.

Как управлять ракетой в полете? Как делать ее полет устойчивым и целенаправленным? Эти вопросы стали актуальными в 30-е годы. Ракеты уже взлетали: и наши, и немецкие "Фау", но в воздухе они вытворяли безумные пируэты, ежесекундно грозя превратиться в чудовищный бумеранг. Не было ни теории правления, ни самих средств управления. После войны круг вопросов расширился: а как управлять спутником в космосе, в невесомости, где нет ни внешней среды, ни точки опоры? Как сориентировать космический аппарат в данном направлении? Ведь, летя по инерции, он кувыркался во всех мыслимых направлениях! Впереди снова открывалось белое поле нерешенных проблем.

Вот этим проблемам Б. В. Раушенбах посвятил свою жизнь, пройдя путь от инженера до академика. С новыми полетами в космос появлялись и новые системы, новые проблемы. Если первые три спутника еще не имели системы ориентации кувыркались в полете, как слепые котята, то ровно через два года после запуска первого спутника, 4 октября 1959 г., межпланетной автоматической станки "Луна-3" была блестяще решена задача управления ориентацией станции. "Луна-3", как известно, облетела Луну, сфотографировала ее с обратной стороны передала изображение на Землю. Так человечество впервые увидело загадочную обратную сторону своего спутника, этом были "Венеры" и "Марсы", "Востоки" и "Восходы", "Молнии" и "Горизонты", "Союзы" и "Салюты". И с каждой новой станцией, новым кораблем вырастали все новые и новые проблемы.

Работа над проблемой стыковки космических кораблей "Союз" пробудила интерес Б. В. Раушенбаха к... живописи. Откуда такие неожиданные параллели? Дело в том, что на корабле "Союз" нет переднего иллюминатора (на его месте расположен стыковочный узел). Поэтому для наблюдения во время стыковки за другим кораблем установлены специальные оптические приборы типа перископов и телекамер, которые, как известно,-дают изображение по законам геометрической оптики, т. е. в линейной перспективе. Но вот тут-то и возникает вопрос: а можно ли доверять этим изображениям? Насколько точно они передают ощущение пространства, видимого непосредственно глазом? Насколько перспектива оптическая, линейная, отличается от перспективы видимой, перцептивной? Ведь стыковка двух кораблей, происходящая на первой космической скорости, требует фантастической точности!

Посещение музея Рублева стало последней каплей в чашу "перспективных" вопросов: у Раушенбаха появилось новое увлечение - геометрия живописи.

Мы уже упоминали о существовании двух геометрических пространств: реальном и перцептивном (с. 297). Перцептивное пространство возникает в нашем сознании в результате совместной работы глаз и мозга. На первом этапе на сетчатке глаза возникает изображение реального пространства, которое подчиняется законам геометрической оптики, т. е. линейной перспективы. На втором - это изображение преобразуется в нашем сознании в результате деятельности мозга. Таким образом, линейная (ренессансная!) перспектива учитывает только работу глаза, но не учитывает работу мозга. Вот где корни излишней "фотографичности" ренессансных полотен!

Какие же коррективы вносит мозг в сетчаточное (линейно-перспективное) изображение? Во-первых, заметим, что в линейно-перспективном изображении близкие предметы выходят чрезмерно большими, а далекие - слишком маленькими. Если бы такое изображение непосредственно передавалось в мозг, то, как отмечает Раушенбах, "человек мог бы испугаться близко сидящего котенка и остаться равнодушным к показавшемуся тигру". Поэтому сетчаточный образ в мозгу корректируется с учетом других признаков глубины пространства (таких, как заслонение близкими предметами далеких, "воздушная" перспектива, бинокулярные признаки). Корректировке подвергаются прежде всего сетчаточные образы малоудаленных предметов как наиболее необходимых в жизнедеятельности человека. В результате образы близких предметов становятся более похожими на их реальные прообразы, воспринимаемая величина близких предметов остается почти неизменной (константной), откуда и проистекает название этого корректирующего механизма работы мозга - механизм константности величины.

Другим важнейшим механизмом работы мозга, преобразующим сетчаточный образ, является механизм константности формы. Суть этого механизма заключается в том, что на сравнительно малых расстояниях знакомые человеку формы кажутся ему почти такими, какими они являются реально, а не такими, каковыми они изображаются на сетчатке глаза. Поясним сказанное примером. Известно, что в линейной перспективе (т. е. на сетчатке глаза) круг или квадрат, если смотреть на них под углом, изображаются как эллипс или трапеция. Однако если человек заранее знает истинную форму рассматриваемых предметов, то они кажутся ему более близкими к их реальной форме: эллипс видится "более круглым", а трапеция - "более квадратной". В этом и состоит суть механизма константности формы. Вот почему, интуитивно осознавая действие механизма константности формы, даже такие последовательные перспективисты, как Дюрер или Рафаэль, никогда не изображали шар в виде эллипсоида, а всегда в виде шара (см. "Меланхолию" Дюрера на с. 42 или "Афинскую школу" Рафаэля на с. 55).

Итак, перцептивное изображение, корректирующее линейный (сетчаточный) образ, существенно отличается от последнего. Это отличие сказывается прежде всего в увеличенных размерах удаленных предметов (например, цепи гор на горизонте), повышенной линии горизонта, сохранении метрических свойств ближних предметов. Последнее особенно важно для живописи: параллельные линии переднего плана в перцептивной перспективе выглядят параллельными. Более того, бинокулярность зрения может привести к тому, что параллельные линии переднего плана покажутся слегка расходящимися! Но ведь это же есть обратная перспектива!

К сожалению, вопрос об истоках обратной перспективы не решается так просто. К нему мы еще вернемся. А пока резюмируем сказанное рисунками, заимствованными нами из книги Б. В. Раушенбаха "Пространственные построения в древнерусской живописи". На рисунке сравниваются линейная (а) и перцептивная (б - монокулярная, в - бинокулярная) перспективы. Предполагается, что основание картины совпадает с горизонтальной поверхностью земли и, следовательно (как и на рис., с. 281), ширина дороги в основании картины (жирная линия) является ее истинной шириной. Характерные особенности каждой перспективы очевидны из рисунка.

Проводя математический анализ представленных перспективных изображений (для нас этот "анализ" сведется к сравнению всех трех рисунков), Раушенбах приходит к следующему выводу:

1) для среднего плана картинного пространства перцептивная перспектива практически совпадает с линейной: дальний план линейная перспектива преуменьшает;

2) для очень близкого и не слишком протяженного плана (т. е. оставаясь в области константности величины) или для очень далекого и не слишком большого объекта (т. е. для объекта с малыми угловыми размерами, для которого схождение параллельных пренебрежимо мало) перцептивная перспектива практически совпадает с аксонометрией;

3) при бинокулярном зрении возможен эффект "сверхконстантности" величины, когда для очень близкого и не слишком протяженного плана перцептивная перспектива, обычно совпадающая с аксонометрией, может принять вид обратной перспективы.

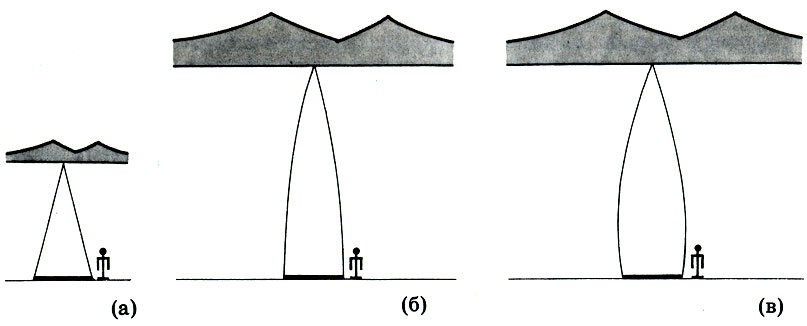
Изображение дороги и цепи гор на горизонте в линейной перспективе (а), перцептивной монокулярной (б) и бинокулярной (в) перспективе. Рисунок Б. В. Раушенбаха

Таким образом, все известные в живописи перспективные системы: параллельная, прямая и обратная - оказываются соответствующими частными случаями перспективы перцептивной.

Таковы современные психофизиологические представления о механизме зрения, с которых Раушенбах подошел к геометрическим загадкам древнерусской иконографии. Раушенбах исходил из естественного предположения о том, что древнерусский художник изображал мир таким, каким он его видел, т. е. в перцептивной перспективе. В самом деле, сам уровень развития средневековой науки и искусства говорит о том, что древнерусский художник не мог подобно художнику ренессансному пользоваться научно разработанной системой перспективы, а творил по наитию, т. е. как видел.

От того, как творил древнерусский мастер, перейдем к тому, что он творил. Слово "икона" в переводе с греческого означает образ, изображение. В центре внимания иконы было изображение Христа, Богоматери, святых и сцен из их жизни. Следовательно, в иконе господствовал "портрет", ближний план, и практически не было пейзажа, плана дальнего. Но согласно второму выводу перцептивная перспектива ближнего, не слишком протяженного плана практически совпадает с аксонометрией.

Так Раушенбах приходит к теоретическому выводу о том, что перспективной основой древнерусской живописи является аксонометрия. Перспективная основа - это еще не система перспективы, а только некоторое приближение к ней, приближение, допускающее разного рода отклонения. Этот вывод подтверждается анализом древнерусской живописи. Например, мы знаем, что подножие правого ангела в "Троице" Рублева дано в аксонометрии, а в изображении левого подножия допущено отклонение в сторону обратной перспективы. Более яркой иллюстрацией к сказанному является новгородская икона "Введение во храм", в которой аксонометрическая основа живописи очевидна. Но и здесь также хорошо видно, что древнерусский иконописец не был педантом от аксонометрии и легко допускал отклонения как в сторону прямой, так и в сторону обратной перспективы.

И все-таки отклонения в сторону обратной перспективы в древнерусской живописи преобладали. Чем же они были вызваны? На этот трудный вопрос нет однозначного ответа. Б. В. Раушенбах называет пять причин появления обратной перспективы:

1. Действие механизма константности формы. Мы знаем, что благодаря действию этого механизма форма знакомого предмета воспринимается человеком не как ее сетчаточный образ, а более близкой к реальным очертаниям этой формы. А как механизм константности формы "действует" на художника? Чтобы прояснить этот вопрос, Раушенбах рассматривает простой пример изображения параллелепипедов табурета и Евангелия, которые были излюбленными атрибутами древнерусской иконографии. На рисунке а показана аксонометрия этих предметов. Однако под действием механизма константности формы художник видит верхнюю крышку табурета (боковые грани книги) более плоско, ближе к их истинной форме, как показано штриховой линией на рисунке а. Но тогда сразу возникают трудности.

Введение во храм. Новгородская икона. XV в.

В случае с табуретом можно показать его ножки, как и раньше, в аксонометрии (рис. б). Однако тогда возникает впечатление, будто ножки табурета повисли в воздухе. Отчего это происходит? Дело в том, что механизм константности формы действует лишь на материальные, видимые, предметы, форма которых заранее известна. А мыслимый квадрат, в углах которого ножки касаются пола, есть нечто абстрактное. Механизм константности формы не должен "поднимать" ножки табурета, они остаются на месте, и тогда возникает обратная перспектива табурета (рис. в). В такой обратной перспективе изображен табурет левого ангела в "Троице" Рублева. Еще лучше ее видно на миниатюре из Евангелия XVI века.

В случае с Евангелием механизм константности формы приводит к разрыву боковых сторон книги (рис. б). Однако даже самый смелый современный художник не позволяет себе допускать разрывы там, где хорошо известно, что изображаемая форма непрерывна. Не мог себе такой вольности позволить и древнерусский иконописец. Поэтому он "склеивает" боковые грани книги некоей средней линией, и в результате получается обратная перспектива Евангелия (рис. в). Такие изображения мы встречали на с. 313.

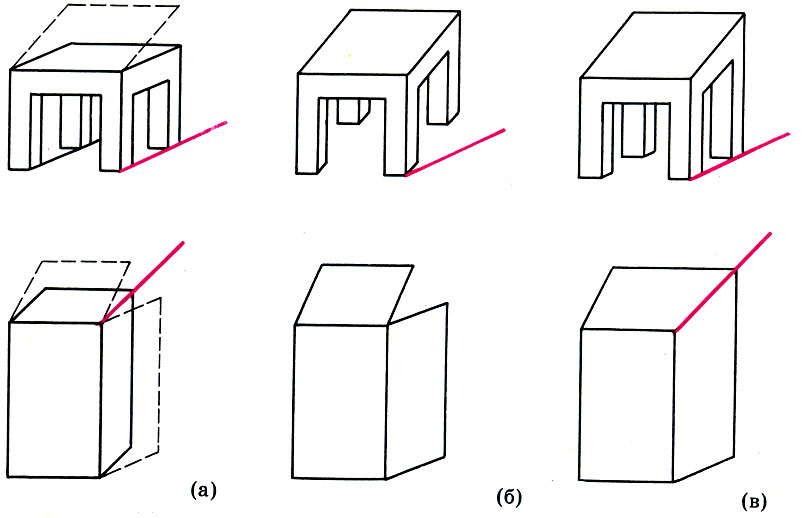
Схема возникновения обратной перспективы (по Б. В. Раушенбаху). Аксонометрическое изображение (а), действие механизма константности формы (б), обратная перспектива (в)

2. Учет бинокулярности зрения. Сегодня экспериментально установлено, что на небольших расстояниях бинокулярность зрения может привести к эффекту слабой обратной перспективы. Этот факт для нас, с детства воспитанных на линейной перспективе фотоаппарата, кино и телевидения, а также на прямой ренессансной перспективе, кажется парадоксальным. Даже в песенке поется о том, что "рельсы, как и водится, у горизонта сходятся", а тут вдруг расхождение параллельных! Но факты - вещь упрямая. Более того, существуют способы, позволяющие натренировать свой глаз на обратную перспективу. Такой "обратноперспективный" взгляд имеет, например, Б. В. Раушенбах.

Но тогда становится совершенно понятным и естественным, что древнерусский художник, еще не отягощенный канонами прямой ренессансной перспективы, рисовал ближний план таким, каким он его видел, т. е. в легкой обратной перспективе. В дальнейшем, правда, обратная перспектива часто принимала гипертрофированные формы. Но это можно понять, если учесть, что обратная перспектива стала своеобразным художественным каноном, а древнерусский иконописец никогда не писал с натуры.

Самые же удивительные открытия, касающиеся обратной перспективы, были сделаны в самое последнее время. В 1947 г. немецкий ученый, работавший в США, Р. Лунберг, опираясь на экспериментальные данные, построил математическую теорию, из которой следовало, что для участков горизонтальной плоскости, находящихся в непосредственной близости от наблюдателя, свойства перцептивного пространства могут быть описаны как свойства риманова пространства постоянной отрицательной кривизны, т. е. как свойства пространства Лобачевского. Тогда, согласно геометрии Лобачевского, всякий прямоугольник ABCD, у которого AD является ближней к наблюдателю стороной, а ВС - дальней, отобразится в перцептивном пространстве в так называемый четырехугольник Ламберта А'В'C'D' стороны которого удовлетворяют неравенству B'C'>A'D'. Следовательно, "дальняя" сторона четырехугольника Ламберта В'С' будет больше его "ближней" стороны A'D'. Но это же и есть обратная перспектива! Древнерусская икона и геометрия Лобачевского! Поистине нет предела удивительному на перекрестках науки и искусства!

3. Подвижность точки зрения. Как отмечалось в сноске на с. 313, даже мастера Возрождения, свято чтившие правила линейной перспективы, позволяли себе совмещать на одном полотне несколько точек зрения. Это была жертва геометрии в пользу искусства; она усиливала впечатление от картины, полнее раскрывала замыслы художника. Древнерусский иконописец, весьма вольно обращавшийся с геометрией живописи, тем более мог позволить себе не одну точку зрения.

Надо сказать, что подвижность точки зрения, в особенности при передаче ближнего пространства, имеет весьма веские причины. Дело в том, что поле четкого зрения человека невелико. Поэтому при осмотре пространства, особенно близкого, мы часто меняем направление осмотра, а иногда и саму точку зрения. В результате близкое пространство мы воспринимаем как совокупность нескольких перцептивных пространств, а значит, и нескольких локальных аксонометрий.

4. Увеличение информативности картины. Мы знаем, что коммуникативная функция играет важнейшую роль в искусстве. Мы видели также, что стремление к наибольшей информативности картины не останавливало древнеегипетского художника перед явными геометрическими казусами: совмещение двух видов в изображении человека (фигурка жреца на с. 266) или соединение нескольких проекций при передаче пространства (Осирис у пруда, с. 300). Все эти геометрические вольности преследовали единственную цель - увеличение информативности картины. Эти же причины часто приводили древнерусского иконописца к обратной перспективе.

Обратимся еще раз к иконе "Митрополит Алексий в житии". Желая показать на нижних клеймах иконы не только гроб, но и возложенное в него тело, Дионисий приподнимает дальнюю от зрителя стенку гроба, что приводит к сильной обратной перспективе. Также и на миниатюре Дионисия младшего. Стремясь подробнее показать содержание записи евангелиста, художник искусственно разворачивает его фолиант к зрителю, что опять-таки создает эффект обратной перспективы.

Дионисий младший. Миниатюра из Евангелия. XVI в.

Новозаветная Троица. Икона XVI в.

Аналогичных примеров, когда поверхности книг с записями, поверхности столов с яствами и вообще горизонтальные поверхности с расположенными на них предметами "информационно" повернуты к зрителю в древнерусском искусстве немало. Все эти "информационные развороты" приводят к эффекту обратной перспективы.

5. Композиционные требования. Анализируя геометрические загадки древнерусской живописи, нельзя забывать, что средневековый иконописец был не только и не столько повествователем, стремящимся наиболее правдиво и наиболее информативно поведать о своем предмете, но прежде всего художником. Не только мера - геометрия, но и красота - искусство двигает рукою всякого истинного художника. В попытках наилучшим образом построить композицию картины, художник не по геометрическим или информативным, а по чисто художественным причинам мог обратиться к обратной перспективе, которая так или иначе становилась идейно-эстетической системой художественного языка древнерусской живописи.

Таковы основные причины возникновения обратной перспективы в древнерусской живописи, названные Б. В. Раушенбахом.

Именно так часто и воспринимал близкое пространство древнерусский художник: левую часть иконы он показывал с правой точки зрения, а правую - с левой. Так поступил Андрей Рублев в своей "Троице". Так поступали и многие другие безвестные иконописцы. В результате изображение становилось более "объемным": оно как бы разворачивалось перед зрителем, переводя его взгляд с одной точки зрения на другую.

Однако неизбежной была и плата за такую геометрическую вольность: там, где сходились две аксонометрии - левая и правая, возникала сильная обратная перспектива. Такую перспективу мы видим в изображении престола на иконе "Новозаветная Троица". Такая же сильная обратная перспектива угадывается и в рублевской "Троице". Однако Рублев мудро задрапировал этот геометрический дефект одеждами ангелов, и он явно не бросается в глаза.

Итак, "склейка" левой и правой аксонометрий являлась источником сильной обратной перспективы.

Необходимо отметить многообразие и разнородность источников обратной перспективы, среди которых есть и причины, никак не связанные с геометрией живописи. Тем не менее, действуя в совокупности, они привели к возникновению нового своеобразного стиля, в котором обратная перспектива стала геометрической основой.

Заметим, что обратная перспектива так и не стала единой геометрической системой древнерусской живописи, подобно линейной перспективе в живописи эпохи Возрождения. Но эта геометрическая непоследовательность придает древнерусской живописи удивительную открытость и очарование, мудрое отрешение от мелочной суетности, некую неопределенность и недосказанность, которые так свойственны истинным произведениям искусства.

Расставаясь с древнерусским искусством, вернемся еще раз к его шедевру, к тому, что "недосказал" Рублев и о чем веками продолжают "догадываться" его наследники. Предоставим слово Б. Раушенбаху: "Не изобразив боковых сторон престола, Рублев сознательно оставил поставленный вопрос без ответа. Представляется правдоподобным, что отмечавшаяся всеми исследователями творчества великого русского художника многогранность содержания "Троицы" требовала и "многогранной", т. е. не до конца определенной, геометрии изображения, чтобы эта геометрия "жила" и "изменялась", поворачиваясь то одной, то другой своей гранью, как и вложенные в "Троицу" идеи".

Но на древнерусском искусстве увлечение Раушенбаха живописью, точнее математикой живописи, не закончилось. Не только древние черные доски, но и яркие полотна мастеров XIX и XX веков таили в себе немало геометрических загадок. В какой перспективе творили Сезанн и Ван Гог, Поленов и Верещагин, Серов и Бенуа? Пока ясно было только одно: отнюдь не в ренессансной. Но тогда в какой? И снова вопросы, вопросы, вопросы.

Из этих вопросов и родилась общая теория перспективы. Новая теория учитывала не только законы геометрической оптики, по которым видит глаз, но и закономерности работы мозга при зрительном восприятии. Последние закономерности невозможно выразить на языке геометрии с помощью проектирования прямыми или искривленными лучами зрения, поэтому новая теория перспективы носит аналитический характер.

Переход к аналитическим методам математического описания вообще отражает процесс более глубокого проникновения математики в ту или иную область знания. В данном случае этот переход означает качественно новое математичекое описание механизма зрительного восприятия. В отличие от ренессансной системы в общей теории перспективы образа точки трехмерного пространства на картинной плоскости находится не путем геометрических построений, а путем вычислений.

Конечно, геометрические построена для художника более удобны и вряд ли найдется художник, который будет расчитывать пространство своей картин! Но теория и создавалась не для этог Новая теория позволила решить задач принципиально недоступную для рене сансной: количественно оценить отклонние полученного изображения от естесвенного зрительного восприятия и на основании этих количественных оценс дать качественное заключение о xapaктере допускаемых искажений (уточнит где преобладают ошибки: в передаче мен штаба изображения, либо в передаче глубины пространства, либо в подобии избражения). А уже на основании эти качественных оценок можно дать прость и удобные геометрические приемы пстроения перспективных изображений.

Мы не будем в самом конце книг утомлять читателя математическими выкладками общей теории перспективы которые к тому же отнюдь не элементарны и требуют знания дифференциального и интегрального исчисления. Остановимся на выводах и геометрически следствиях, которые вытекают из это теории.

Общая теория перспективы - это тория перцептивного изображения, в основе которой лежат обсуждавшиеся свойства перцептивного пространства. Системы перспективы, построенные на базе oбщей теории перспективы, будем назвать научными системами перспективы. Главный вывод, к которому приходит Б. В. Раушенбах, таков: не существует идеальной научной системы перспективы. Существует бесчисленное множество равноправных систем перспективы, каждая из которых содержит свои неизбежные ошибки изображения. Все системы отличаются друг от друга тем, на какие элементы изображения смещены эти ошибки, что и может в зависимости от художественных задач служить критерием выбора той или иной системы перспективы.

Этот вывод является частным случаем более общего математического факта: невозможно взаимнооднозначно и непрерывно отобразить трехмерное пространство на двумерную плоскость. Хотя на первый взгляд это кажется и странным, но взаимнооднозначное отображение пространства на плоскость возможно. Образно говоря, можно "истолочь" пространство на бесконечно малые точки и рассыпать эти точки бесконечно тонким слоем нa. плоскости. Однако при этом безвозвратно нарушается строение пространства, близкие элементы пространства не перейдут в близкие элементы плоскости, т. е. отображение не будет непрерывным. Разумеется, подобные отображения для изобразительных целей неприемлемы, ибo изобразительное искусство прежде всегo интересует именно форма. Рассмотренные нами способы проецирования пространства на плоскость (ортогональные проекции, аксонометрия, центральные проекции), равно как и научные системы перспективы, являются своеобразным компромиссом между взаимнооднозначностью и непрерывностью отображения пространства на плоскость. Аналогичное противоречие между "содержанием" (взаимнооднозначность) и "формой" (непрерывность) отображения приходится разрешать, например, в картографии при отображении сферы Земли на плоскость карты. Эта задача также не имеет "идеального" решения.

Проанализировав различные варианты научных систем перспективы, Раушенбах пришел к своеобразному "закону сохранения искажений в изобразительном искусстве". Суть этого закона, который наиболее ярко проявляется при изображении интерьера, т. е. не слишком протяженного пространства, заключается в том, что суммарная ошибка при передаче изображения для любой системы перспективы оказывается практически одной и той же. До обнаружения этого неожиданного факта казалось, что научная система перспективы должна носить абсолютный характер, так как она исходит из объективных законов природы (законов работы глаза и мозга). А оказалось, что научных систем перспективы сколь угодно много и все они с точки зрения математики (по суммарной ошибке искажений) равноценны. Поэтому проблема выбора подходящего варианта научной перспективы становится проблемой эстетической. Вот что по этому поводу пишет Раушенбах: "Эстетика "вторглась", казалось бы, в строго математическую область с неожиданной стороны... Именно эстетические соображения отбирают из бесчисленного множества предлагаемых математических вариантов тот, который является наиболее подходящим для решаемой художественной задачи".

"Закон сохранения искажений" еще раз убеждает нас в поразительной мудрости природы. Ведь если бы удалось найти систему перспективы, наиболее адекватную зрительному восприятию, то искусство живописи (по крайней мере, для художника-реалиста) должно было бы остановиться! Художнику не оставалось бы ничего, кроме как честно следовать этой наилучшей системе. И вот математика доказывает, что такой системы попросту нет, и последнее слово вновь остается за искусством!

Каковы же они, возможные научные системы перспективы? На рисунке показаны три варианта изображения условного пейзажа, взятые из книги Б. В. Paушенбаха "Системы перспективы в изобразительном искусстве. Общая теория перспективы". Горизонтальная поверхность Земли для большей наглядности разграфлена прямоугольной координатной сеткой. К цепи гор на горизонте ведет "дорога", проходящая по диагоналям прямоугольников. Вертикальные масштабы, построенные по правилам каждого варианта, показаны черными шестами, а прилегающие к ним белые шесты обозначают вертикальные размеры, соответствующие естественному зрительному восприятию. Все рисунки построены не "от руки", а рассчитаны согласно общей теории перспективы.

Вариант (а) соответствует системе перспективы, безошибочно передающей поверхность Земли (ширину и глубину пространства), а также дальний план (горы). Как видно из сравнения белых и черных шестов, неизбежные ошибки в этой системе смещены на вертикали, причем наибольшие ошибки допускаются при изображении вертикалей переднего плана, а по мере удаления к горизонту эти ошибки убывают. Здесь может воз никнуть естественный вопрос: а почему бы в этой системе, правильно передаю щей горизонтальные размеры, не пока зывать в соответствии с естественным восприятием и вертикальные линии? Тог да бы эта система стала "идеальной"? Однако такое насильственное вторжение в строение научной системы перспективы обернется тем, что при передаче полного пространства в изображении непрерыв них элементов появятся либо разрывы либо наложения одних элементов на другие. Подобные дефекты недопустимы, и поэтому в данном случае приходится жертвовать вертикалями.

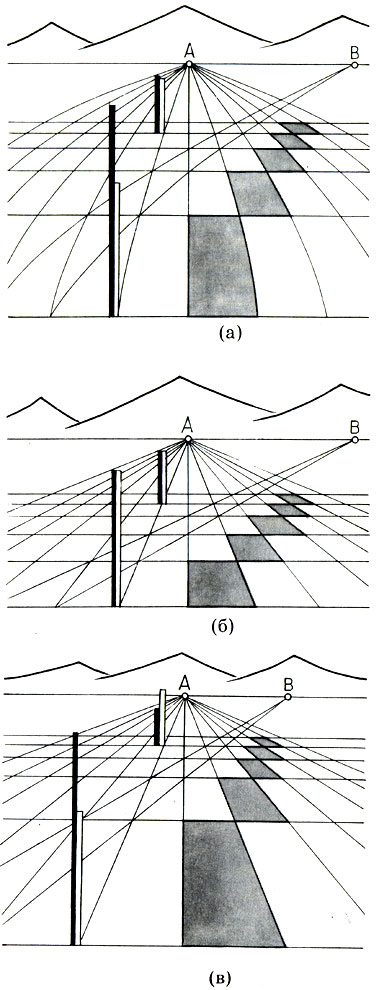
Возможные варианты научной перспективы: (а) - правильная передача поверхности земли; (б) - правильная передача вертикальных размеров; (в) - ренессансная перспектива. Рисунки Б. В. Раушенбаха

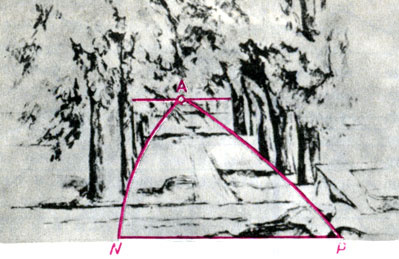
Сезанн. Каштановая аллея в Жа де Буффан. 1883-1887. Перспективный анализ Б. В. Раушенбаха

В варианте (б) ошибки в передаче вертикальных размеров исправлены. Более того, в этой системе правильно передается и ширина, а значит, сохраняется подобие фронтальных изображений. Однако какой "ценой" все это достигнуто, очевидно из самого рисунка: на нем крайне невыразительно, ослабленно передана глубина пространства, особенно глубина переднего плана.

Наконец, на рисунке (в) тот же условный пейзаж передан в ренессансной (линейной) системе перспективы. Сравнение этого рисунка с вариантами (а), (б) выявляет главный недостаток ренессансной системы: сильное преувеличение переднего плана и явное преуменьшение дальних объектов. Этот недостаток ренессансной (а значит, и фотографической) перспективы хорошо знаком альпинистам: запечатлев себя на фоне грандиозной горной панорамы, дома они обнаруживают на пленке жалкую гряду холмов на горизонте. Для среднего плана все ошибки ренессансной перспективы практически равны нулю.

Таким образом, анализ ошибок, неизбежно возникающих в той или иной системе перспективы, позволяет определить границы применимости известных систем перспективы и сделать выводы, которые были приведены на с. 317.

Анализ ошибок при изображении пейзажа (глубокого пространства) показывает, что в любой системе перспективы наибольшим искажениям подвержен именно передний план. Этот "закон наибольших искажений переднего плана" хорошо осознан художниками на практике. Поэтому при изображении пейзажа опытные мастера либо "отсекают" передний план границами картины, либо погружают его в тень.

Обратим внимание на то, что в варианте перспективы, правильно передающем глубину пространства (рис. а), образы прямых линий, уходящих к горизонту, становятся криволинейными (см. координатные линии, сходящиеся в точке А, и "дорогу"). Это свойство перспективы, правильно передающей глубину, было интуитивно "нащупано" некоторыми художниками XIX-XX вв., которые стали умело им пользоваться. А вот искусствоведы, подходившие к анализу живописи с позиций ренессансной системы перспективы либо приводившие в качестве аргументов фотографии (но это также линейная перспектива!), продолжали обвинять таких художников в своеволии и отступлении от "научных" канонов линейной перспективы.

Особенно "не повезло" здесь Полю Сезанну (1839-1906), чьи пейзажи в специальной монографии были тщательно сравнены с соответствующими фотографиями и где были указаны все его "ошибки". Возьмем, к примеру, акварель Сезанна "Каштановая аллея в Жа де Буффан". Эта акварель удобна для перспективного анализа тем, что ряды каштанов в натуре заведомо прямолинейны. Однако на акварели они явно искривлены, что и позволило сделать скоропалительный вывод о том, что Сезанн отступал от натуры. Однако, как показал Раушенбах, криволинейный треугольник ANP в соответствующем масштабе с удивительной точностью вписывается в криволинейную сетку координат на рисунке а (с. 325). Таким образом, именно горизонтальная поверхность Земли (а значит, и ряды каштанов) переданы Сезанном в полном соответствии со зрительным восприятием^*.

^* (Справедливости ради следует отметить, что Сезанн действительно иногда отступал от зрительных ощущений. Так, он часто преувеличивал размеры горы св. Виктории, которую ему хотелось видеть похожей, скорее, на гималайскую вершину. )

Не менее убедительным оказывается и сделанный Раушенбахом перспективный анализ этюда В. Д. Поленова (1844-1927) "Церковь св. Елены". Этот этюд был написан Поленовым в 1882 г. во время путешествия по Ближнему Востоку. В ренессансной системе перспективы (или на фотографии) образы параллельных линий равной высоты, проходящих по карнизам колонн и через середины (верхние точки) трех арок, должны быть прямолинейными. Как видно из иллюстрации, эти линии на этюде сильно искривлены. Пересекаясь на линии горизонта, они указывают на истинную главную точку картины, отмеченную кружком. Столь сильное искривление образов объективно прямых линий вызвано тем, что в изображаемом интерьере передний план вплотную приближен к зрителю. Однако такая геометрия этюда Поленова также не является "перспективной ошибкой", а, напротив, хорошо согласуется с вариантом (а), правильно передающим глубину пространства.

Эти два примера убеждают в том, что художники прежде всего предпочитают те варианты научной перспективы, которым свойственна правильная передача глубины пространства. Но это и понятно, ибо именно здесь решается извечный парадокс живописи: убедительно изобразить трехмерное пространство мира (а значит, прежде всего показать глубину пространства) на двумерной плоскости картины.

Еще раз отметим, что с позиций общей теории перспективы с помощью математического анализа ошибок изображения удалось строго указать границы применимости таких двух систем перспективы, как аксонометрия и слабая обратная перспектива. Эти две системы при определенных условиях (см. с. 318) являются совершенно естественными и равноправными вариантами научной системы перспективы. Аксонометрия и слабая обратная перспектива являются хорошими способами передачи формы и объема отдельного предмета, а не целостного пространства. При этом аксонометрия является счастливым исключением, абсолютно безошибочно передающим близкие и не слишком протяженные объекты. Так, в рамках общей теории перспективы обрели свое место аксонометрия и обратная перспектива, не имевшие прежде теоретического фундамента, но сыгравшие выдающуюся роль в истории искусства (см. гл. 22).

В. Поленов. Церковь Св. Елены. 1882. Перспективный анализ Б. В. Раушенбаха

Книга Б. В. Раушенбаха "Системы перспективы в изобразительном искусстве. Общая теория перспективы" вышла в свет в 1986 г. До этой книги в течение почти 500 лет не появлялось фундаментальных трудов по перспективе! Проблема перспективы казалась решенной раз и навсегда еще в XV веке! И вот в конце XX века появляется труд, автор которого исходит из того, что не было известно науке XV века - математического анализа, дифференциальных уравнений, геометрии Лобачевского - и что так и осталось недоступным искусствоведам века XX. Только человек, соединяющий в одном лице глубокое знание математики с тонким чувством прекрасного, мог сделать это открытие!

Спираль науки сделала гигантский виток длиной в 500 лет и на качественно новом уровне решила, казалось бы, старую, как мир, задачу. Но вряд ли стоит думать, что все точки над i в теории перспективы расставлены окончательно. Пути науки, как и пути искусства, не имеют "точек схода", они простираются в бесконечность.