21. В плену, в Саратове: рождение проективной геометрии

В деревню, к тетке, в глушь, в Саратов! 
Там будешь горе горевать...

А. Грибоедов

1812 год. Ноябрь. Истерзанная Бородинским сражением, испуганная московскими пожарами, измученная отсутствием продовольствия и фуража, "великая армия" Наполеона отступала. Впрочем, не отступала - бежала. Так и не дождавшись ключей от Москвы, не сумев пробиться в южные районы России, император молча скакал по им же разоренной Смоленской дороге. Из-за бескормицы начался падеж лошадей, приходилось бросать артиллерию. Лошади, еще месяц назад оглашавшие ржанием гулкие соборы Московского Кремля, валялись теперь вдоль дороги с раздутыми боками. Непрерывные атаки отрядов атамана Платова и Дениса Давыдова повергали в паническое оцепенение некогда грозную гвардию. Крепчали морозы, и таяла на глазах "великая армия" Наполеона.

3 (15) ноября авангарды генералов М. Милорадовича и Д. Голицына под местечком Красным близ Смоленска внезапно столкнулись с самим Наполеоном. Три дня шли кровопролитные бои, приведшие к разгрому лучших войск Наполеона. Французы потеряли 6 тысяч убитыми и ранеными, 26 тысяч пленными. Армия фактически была брошена императором, голодные и обмороженные солдаты прятались по лесам и далее спасались кто как может. Это была прелюдия к развязке на реке Березине.

Среди оставленных умирать на красном снегу под красным был и двадцатитрехлетний сублейтенант инженерных войск Жан Виктор Понселе. К счастью, дозорный отряд казаков заметил, что молодой "французик" еще дышит. Мундир офицера корпуса инженеров спас ему жизнь. Его подобрали и доставили в русский штаб для допроса.

Затем последовал мучительный 1000-верстный переход вглубь России. Почти пять месяцев нескончаемые вереницы полураздетых и полуживых военнопленных брели по бескрайним заснеженным равнинам. Морозы были так крепки, что ртуть застывала в термометрах. Люди падали и замерзали, не имея сил подняться. В марте 1813 г. Понселе с оставшимися в живых товарищами по несчастью оказался на берегах Волги, в губернском городе Саратове.

Русский народ всегда был велик состраданием. В обмороженных французах сердобольные волжане увидели не бывших врагов, а нынешних страдальцев. Их обогрели, откормили. Яркое апрельское солнце, молодость и жажда жизни победили. Они выжили.

Пленных не обременяли работами. Доподлинно известно лишь то, что они разбили прекрасную дубовую аллею у загородного дома саратовского губернатора. Возможно, один из немногих ныне уцелевших дубов был посажен руками Понселе. Со временем те, кто владел ремеслом, открыли лавки; другие подвизались на ниве воспитания: саратовские красавицы не упускали случая взять уроки модных парижских танцев. Жизнь вошла в свое русло.

Понселе занялся науками. Книг, разумеется, не было, письменные принадлежности - самые скудные. Поэтому прежде всего он восстановил по памяти все, что знал по математике,- от арифметики до математического анализа и высшей геометрии. Вокруг Понселе собирается кружок единомышленников - таких же, как и он, воспитанников Политехнической школы в Париже либо мечтающих выдержать туда экзамен, если когда-нибудь они снова увидят родную Францию. Занятия математикой скрашивали долгие вечера. Любопытно признание самого Понселе в том, что практически все сложные математические выкладки, которые он изучал, стерлись в его памяти, тогда как общие фундаментальные принципы остались в ней такими же ясными, как и много лет назад. Именно за этими занятиями математикой Понселе и пришел к своему гениальному творению - созданию проективной геометрии.

То, что в саратовском плену Понселе вспомнил прежде всего о геометрии, разумеется, не было случайным. Вся французская наука того времени была пронизана духом геометрии. Во главе Политехнической школы, которую Наполеон называл наседкой, несущей ему золотые яйца, стоял отец начертательной геометрии Гаспар Монж. Да и сам император оставил в геометрии несколько теорем, носящих его имя.

Саратовский плен оказался недолгим. 25 марта (6 апреля) 1814 г. Наполеон подписал в Фонтебло отречение от престола и был сослан на остров Эльба. А в сентябре того же года пленники вернулись на родину.

Понселе возвратился во Францию с семью записными книжками, хранившими его блестящие идеи. Именно "материал семи рукописных записных книжек, написанных в Саратове, в русском плену (с 1813 по 1814 г.), вместе с разными другими записями, старыми и новыми", и составил основу классического труда молодого офицера - "Трактат о проектных свойствах фигур". Первое издание трактата вышло в 1822 г. Второму изданию, вышедшему сорок лет спустя, была предпослана "апология" - описание давних приключений автора, имевших самый счастливый конец^*.

^* (Можно лишь с горечью констатировать, что сегодня нам ничего не известно о рукописи другого саратовского пленника, также написанной по памяти, но от которой нас отделяют не более 150, а менее 50 лет. Это рукопись "История развития мирового земледелия" Джордано Бруно XX века - Николая Вавилова, чья звезда так ярко взошла и столь трагически упала в Саратове. )

С выходом в свет трактата Понселе проективная геометрия стала самостоятельной наукой. Заслуга Понселе заключалась в выделении проективных свойств фигур (Понселе понимал их как свойства, которые остаются неизменными при любом центральном проектировании фигуры с одной плоскости на другую) в отдельный класс и установлении соответствий между метрическими и проективными свойствами этих фигур. Помимо точек и прямых проективными свойствами oбладают, например, линии второго порядка (окружности, эллипсы, параболы и гиперболы). Понселе были сформулированы также принцип непрерывности и принцип двойственности. Первый принцип позволил рассмотреть всякого рода исключения и особые случаи с более широкой точки зрения (например, параллельность прямых как пересечение их в бесконечно удаленной точке) и дать геометрический аналог мнимым числам в геометрии. С помощью второго принципа стало возможным в два раза увеличивать число теорем проективной геометрии, не прилагая при этом никаких усилий.

Истинное значение проективных свойств геометрии было осознано лишь в конце XIХ века, когда немецкий математик Феликс Клейн (1849-1925) доказал, что обычная геометрия Евклида, и "необычная" геометрия Лобачевского могут быть ассмотрены в рамках проективной геометрии. Так было установлено кардинальное значение проективной геометрии по всей геометрии.

"Милостивые государи! Между приобретениями, сделанными в области геометрии за последние пятьдесят лет, развитие проективной геометрии занимает свое место". Этими словами в старинном немецком городке Эрлангене в 1872 г. Клейн начал свою знаменитую лекцию, вошедшую в историю математики как Эрлангенская программа". В этой лекции, изменившей взгляд на геометрию в целом, Клейн дал новое определение древней науки: геометрия есть учение об инвариантах той или иной группы преобразований. Выбирая по-разному группу преобразований, можно получать разные геометрии. Заметим, что проективная геометрия лежит в основе теории аэрофотосъемки и находит сегодня важнейшее приложение при обработке снимков из космоса.

Рассмотрим основные идеи проективной геометрии. Как отмечалось в конце предыдущей главы, Понселе возродил идею проективной плоскости Дезарга, т. е. плоскости, дополненной бесконечно удаленными точками и бесконечно удаленной прямой. На проективной плоскости стираются различия между параллельными и пересекающимися прямыми, свойство прямых пересекаться становится инвариантным относительно операции проектирования, а поведение точек и прямых определяется двумя аксиомами (см. с. 285). Поскольку метрические свойства геометрических фигур (расстояния и углы) при проектировании не сохраняются (см. с. 275), а проективная геометрия изучает свойства фигур, инвариантные относительно операции проектирования, то метрические свойства в проективной геометрии не рассматриваются. Именно поэтому проективную геометрию называют "геометрией положения" или "геометрией линейки без делений".

Разумеется, проективная геометрия развилась не вдруг с появлением трактата Понселе. Известны три важнейшие предтечи проективной геометрии - три теоремы элементарной геометрии, которые не содержат в условиях метрических характеристик. Первая теорема известна с глубокой древности и носит имя александрийского геометра III века Паппа.

Теорема Паппа. Пусть l и m - две прямые на плоскости; А, В, С - различные точки прямой l, а А', В', С' - различные точки прямой m. Тогда точки пересечения трех пар накрест лежащих прямых АВ' и А'В, ВС' и В'С, С А' и С'А принадлежат одной прямой. Проективный характер теоремы Паппа очевиден: в ней фигурируют только точки, прямые и их пересечения; поэтому теорема Паппа остается справедлива при любом проективном преобразовании.

Через 1200 лет после Паппа шестнадцатилетний юноша Блез Паскаль (1623-1662) опубликовал свое лучшее математическое сочинение "Трактат о конических сечениях". В трактате Паскаль доказал теорему, которую он назвал Hexagramma mysticum (Волшебный шестиугольник) и которую он украсил почти 400 следствиями. Теорему Паскаля можно считать своего рода обобщением теоремы Паппа на случай конических сечений^*, которые, как и прямые, обладают проективными свойствами.

^* (Коническими сечениями (линиями второго порядка) называют эллипс (и его частный вид - окружность), параболу и гиперболу - линии, которые могут быть получены как сечения прямого кругового конуса. В последнем легко убедиться, посветив обычным карманным фонариком (световой конус) на стену. Когда фонарик перпендикулярен стене, мы видим окружность, затем при наклоне фонарика - эллипс. Когда одна из образующих светового конуса станет параллельна стене, мы Увидим параболу и, наконец, при больших углах наклона - гиперболу. Математическое доказательство этих результатов принадлежит выдающемуся античному математику Апполонию из Перги.)

Теорема Паскаля. Пусть А, В, С, А', В', С' - шесть точек, принадлежащих некоторому коническому сечению. Тогда точки пересечения трех пар накрест лежащих прямых АВ' и А'В, ВС' и В'С, СА' и С'А принадлежат одной прямой. Существует и другая формулировка теоремы Паскаля, в которой ее связь с теоремой Паппа не столь очевидна: три точки пересечения противоположных сторон шестиугольника, вписанного в коническое сечение, лежат на одной прямой (см. с. 294). Еще раз подчеркнем, что теорема Паскаля справедлива для любого конического сечения (окружности, эллипса, параболы и гиперболы). Более того, при надлежащем определении касательной в точке конического сечения теорема Паскаля будет выполняться в том случае, когда не все из шести точек различны.

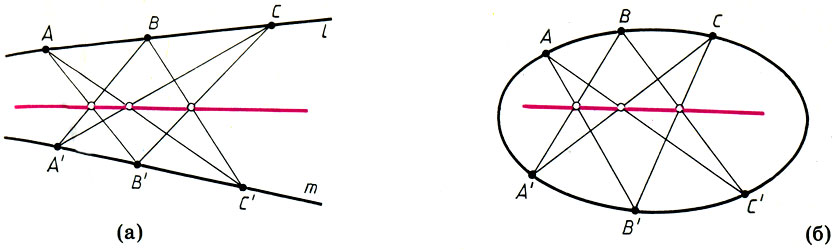
Теорема Паппа (а) и теорема Паскаля (б)

Наконец, третья теорема - одна из важнейших теорем проективной геометрии - носит имя Дезарга, который вместе с Понселе разделяет славу создания проективной геометрии.

Теорема Дезарга. Пусть ABC и А'В'С - два треугольника (необязательно лежащие в одной плоскости), такие, что прямые АА', ВВ' и СС', соединяющие соответственные вершины треугольников, сходятся в одной точке S. Тогда точки пересечения соответственных сторон этих треугольников АВ и А'В', ВС и В'С', СА и С'А' лежат на одной прямой. Плоский вариант теоремы Дезарга, как и теоремы Паппа и Паскаля, отнюдь не очевиден, тогда как ее пространственный вариант настолько прозрачен, что просто удивительно, как художники Возрождения, так много занимавшиеся теорией перспективы, не "заметили" его.

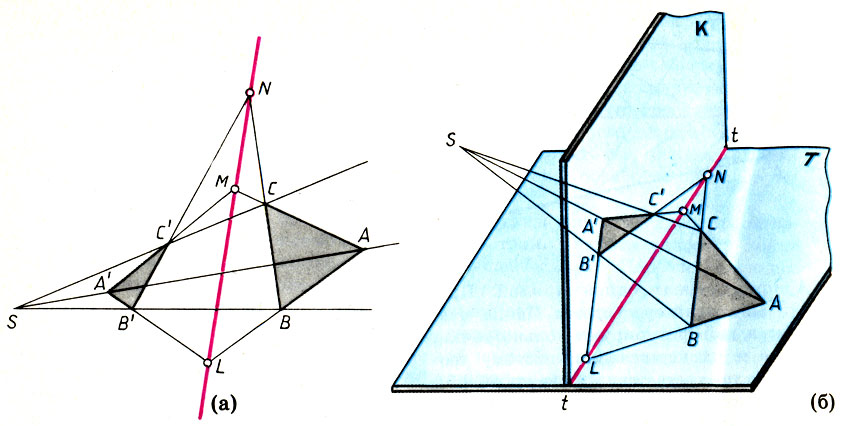
Плоский (а) и пространственный (б) варианты теоремы Дезарга

В самом деле, пусть треугольник ABC лежит в горизонтальной плоскости Т, треугольник А'В'С' есть его изображение на картинной плоскости К и точка S - центр проектирования. Прямые, соединяющие соответственные вершины этих треугольников,- это "лучи зрения", а ΔА'В'С есть сечение "пирамиды зрения" с основанием ABC и вершиной в точке S. Соответственные стороны АВ и А'В' расположены на грани SAB "пирамиды зрения", т. е. лежат в одной плоскости и пересекаются в некоторой точке L. Но точка L одновременно принадлежит прямым АВ и А'В'. Значит, она одновременно принадлежит плоскости Т и плоскости К, т. е. лежит на линии пересечения этих плоскостей - прямой tt. Аналогично доказываем, что и точка пересечения сторон АС и А'С (точка М) и сторон ВС и В'С (точка N) лежат на той же прямой tt. Следовательно, все три точки L, М, N лежат на одной прямой. Пространственная теорема Дезарга доказана.

Для доказательства плоской теоремы Дезарга достаточно ΔА'В'С', лежащий в картинной плоскости К, спроектировать на плоскость Т из двух центров проекции S и S₁ определяющих прямую S¹ S'. В результате на плоскости Т мы получим два треугольника: ABC и А'В'С. Поскольку прямые S₁A" и SA лежат в одной плоскости, то точки А" и А будут лежать на одной прямой S'A - линии пересечения этой плоскости с плоскостью Т (аналогично для точек В" и B, а также С" и С). Следовательно, прямые, соединяющие соответственные вершины треугольников ABC и А"В"С", пересекаются в одной точке S' т. е. удовлетворяют условию теоремы Дезарга. Для каждой из пар треугольников: ΔА'В'С' и ΔАВС, а также ΔА'В'С' и ΔА"В"С" -справедлива пространственная теорема Дезарга. Более того, так как в каждой паре этих треугольников имеется один й тот же ΔА'В'С', то всякий раз все три соответственные стороны этих треугольников будут пересекаться в одной точке. Так мы получим точки L, М и N, лежащее на прямой tt, т. е. придем к плоской теореме Дезарга.

Оба доказательства теоремы Дезарга настолько просты и изящны, что трудно было удержаться от соблазна привести их здесь. Но дело не только в этом. Мы доказали плоскую теорему Дезарга с помощью ее пространственного аналога, т. е. при помощи пространственных построений. Как показал в конце XIX века Д. Гильберт, без выхода из плоскости в пространство вообще невозможно доказать плоскую теорему Дезарга методами проективной геометрии (без привлечения метрических понятий). Следовательно, если задаться целью разрабатывать плоскую проективную геометрию лишь средствами плоскости, не используя пространство, то мы обязаны присоединить теорему Дезарга в качестве новой аксиомы этой плоской геометрии. Затем Гильберт показал, что, исключив "аксиому Дезарга", можно построить новую, так называемую недезар-гову, геометрию на плоскости. Так на протяжении веков раскрывалась чрезвычайно важная роль теоремы Дезарга в проективной геометрии.

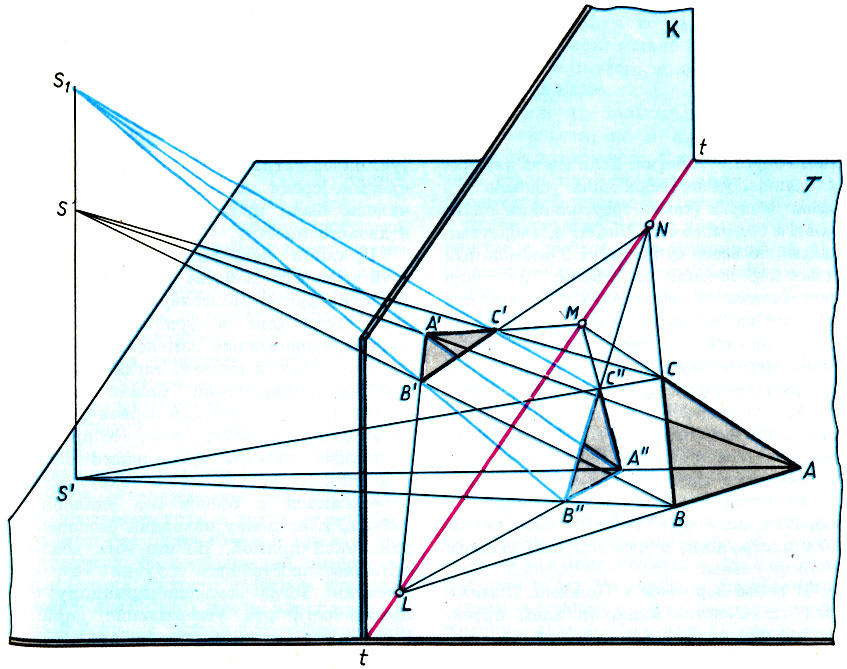
К доказательству плоской теоремы Дезарга

Заканчивая краткое знакомство с тремя великими предтечами проективной геометрии, нельзя не отметить и ту глубокую связь между теоремами Паскаля и Дезарга, которая также была раскрыта лишь спустя столетия. Если взять два треугольника, удовлетворяющих условию теоремы Дезарга (такие треугольники называются гомологическими, т. е. сходственными), то всего существует 9 возможных точек пересечения их сторон. Три точки пересечения соответственных сторон, как следует из теоремы Дезарга, лежат на одной прямой. А вот остальные шесть точек пересечения всегда лежат на некотором коническом сечении, т. е. удовлетворяют теореме Паскаля! Заинтересовавшийся читатель может сам построить массу интересных конфигураций с гомологическими треугольниками.

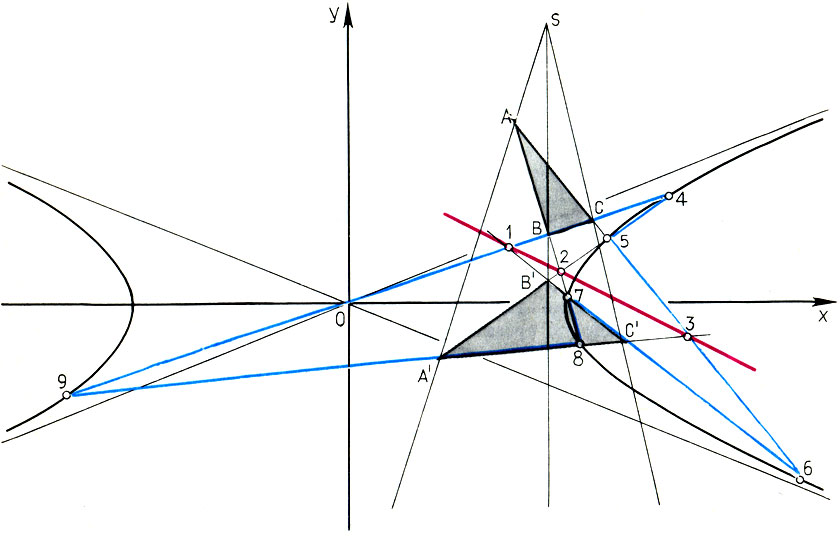
Связь между теоремами Паскаля и Дезарга: из 9 возможных точек пересечения гомологических треугольников ABC и А'В'С' 3 точки пересечения сходственных сторон лежат на одной прямой (точки 1, 2, 3), а остальные 6 - на коническом сечении (гиперболе) - точки 4, 5, 6, 7, 8, 9

Наконец, теорема Дезарга является теоретическим фундаментом перспективных построений, о чем мы еще скажем в конце главы.

И снова вернемся к Понселе. Помимо того что Понселе возродил идею проективной плоскости Дезарга и придал "геометрии положения" самостоятельный статус, он обогатил новую науку и новыми идеями, среди которых, как уже отмечалось, были принципы непрерывности и двойственности.

Принцип непрерывности, позволяющий выводить свойства одной фигуры из свойств другой, Понселе сформулировал так: "Если одна фигура получается из другой непрерывным изменением и столь же обща, как и первая, тогда без дальнейших соображений можно отнести свойства, доказанные для первой фигуры, ко второй". Например, ясно, что противоположные стороны правильного шестиугольника, вписанного в окружность, пересекаются в бесконечно удаленных точках, т. е. лежат на одной бесконечно удаленной прямой. Но это есть доказательство простейшего случая теоремы Паскаля! Тогда согласно принципу непрерывности это утверждение должно быть справедливо и для любого шестиугольника, вписанного в коническое сечение, т. е. мы получаем доказательство общей теоремы Паскаля! Итак, сформулировав и доказав теорему проективной геометрии в простейшем частном случае, Понселе автоматически получал ее обобщение для любой проекции, в которой вид первоначальной конфигурации мог измениться до неузнаваемости.

Несмотря на неточную формулировку, в руках Понселе принцип непрерывности дал новые и верные результаты. Однако на пути применения принципа часто возникали подводные камни. Например, легко видеть, что эллипсы или параболы пересекаются на плоскости в четырех точках, тогда как окружности - только в двух. Между тем как конические сечения эти линии должны обладать одинаковыми свойствами. Вводя на плоскости систему координат и следуя принципу непрерывности, Понселе пришел к выводу, что все окружности помимо двух действительных точек пересечения имеют на плоскости еще две точки пересечения, которые являются не только бесконечно удаленными, но и мнимыми (точнее, комплексно-сопряженными). Так в геометрии появились комплексные числа.

Но если принцип непрерывности достаточно сложен и требует поистине математического полета фантазии, то принцип двойственности прост и прозрачен. Рассмотрим, как действует принцип двойственности в планиметрии.

Вспомним основные аксиомы проективной геометрии на плоскости, формулировка которых стала возможной с введением понятия бесконечно удаленных точек (см. с. 285). Принцип двойственности основан на том простом факте, что эти две аксиомы обнаруживают двойственность, т. е. переходят друг в друга, если поменять местами слова точки и прямые (соответственно из соображений литературности языка следует поменять глаголы лежат и проходят, а также предлоги на и через). Если же, говоря о точке, лежащей На прямой, или о прямой, проходящей через точку, ввести более общий термин прямая и точка инцидентны, то последние языковые различия устраняются и аксиомы проективной планиметрии примут наиболее универсальный вид:

А.1. Две различные точки на проективной плоскости определяют прямую, и притом только одну, которой они обе инцидентны.

А.2. Две различные прямые на проективной плоскости определяют точку, и притом только одну, которой они обе инцидентны.

Теперь эти две аксиомы отличаются друг от друга только выделенными словами, т. е. словами точки и прямые, а мы получаем возможность сформулировать сам принцип двойственности: все утверждения проективной планиметрии образуют пары, в которых одно из утверждений пары можно непосредственно получить из другого, взаимозаменив слова точка и прямая.

Понселе не только открыл принцип двойственности, но и применял его до пределов возможного. С легкой руки Понселе стало принято записывать теоремы проективной геометрии в два столбца: в одном столбце пишут доказанную теорему, а в другом - двойственную ей. Разумеется, доказательство двойственной теоремы становится излишним. Таким образом, с открытием Понселе стало возможным удвоить число теорем проективной геометрии, не затратив при этом никакого труда.

В качестве примера двойственных теорем приведем следующую пару. В левом столбце записана известная нам теорема Паскаля, которая сформулирована в удобном для "двойственного перевода" виде. Дополнив наш "словарь двойственных терминов" еще одной парой: точка пересечения двух прямых и прямая, проходящая через две точки,- мы легко получаем в правом столбце теорему, двойственную теореме Паскаля. (В обеих теоремах взаимозаменяемые термины выделены, а выражения, проясняющие смысл, взяты в скобки.)

Если А, B, С, D, Е, F - любые точки конического сечения, то три точки пересечения двух противоположных прямых (сторон вписанного шестиугольника) инцидентны одной прямой. Теорема Паскаля

Если А, В, С, D, Е, F - любые прямые (касательные) к коническому сечению, то три прямые, проходящие через две противоположные точки (вершины описанного шестиугольника), инцидентны одной точке. Теорема Брианшона

Каков же был восторг Понселе, когда в теореме, двойственной теореме Паскаля, он увидел теорему, доказанную в 1806 г. его однокашником, студентом Политехнической школы Шарлем Брианшоном (1785-1864)! Однако в отличие от Брианшона Понселе доказывал эту теорему "автоматически". Это открытие утвердило Понселе в могуществе принципа двойственности.

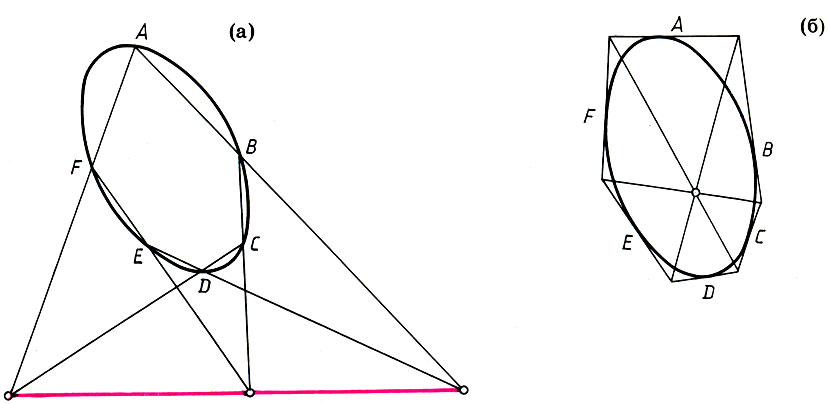
Принцип двойственности: теорема Паскаля (а) и теорема Брианшона (б)

И в заключение вновь перейдем от математики к искусству. Рождению проективной геометрии во многом способствовали геометрические исследования художников Возрождения. А появившись на свет, проективная геометрия стала теоретическим фундаментом искусства перспективы. Важную роль при построении перспективных изображений играет теорема Дезарга. Мы остановимся на двух приложениях этой теоремы к теории перспективы.

Теорема Дезарга и способ архитекторов. Способ-архитекторов, который мы применили в предыдущей главе для построения перспективы интерьера комнаты и перспективы параллелепипеда (см. с. 282), состоит, по существу, в построении двух точек: точки схода изображаемой линии и точки пересечения этой линии с основанием картины. Зная эти две точки, мы можем построить перспективное изображение данной линии. Метод построения точки схода на перспективе был нами разобран на с. 279, доказательство его справедливости очевидно из рисунка на с. 281. А вот найти точку пересечения образа данной линии с основанием картины позволяет нам теорема Дезарга.

Обратимся для определенности к рисунку на с. 282. Прежде всего заметим, что любую фигуру, состоящую из прямых линий, можно разбить на соответствующее число треугольников. Рассмотрим треугольник ABC на плоскости Т (рис. б) и его перспективное изображение треугольник abc на плоскости К (рис. а). По теореме Дезарга соответственные стороны этих треугольников пересекаются в одной точке на основании картины tt. Именно поэтому в наших построениях мы продолжили сторону ВС до пересечения с линией основания tt в точке М (рис. б), а затем перенесли эту точку ни линию tt в плоскости К. Так мы нашли неизвестную нам точку пересечения образа линии ВС с линией основания tt (точка m на рис. а). Аналогично найдена и точка п. Зная точки пересечения m, a, n и их точки схода F_l и F₂, легко построить перспективу прямоугольника ABCD.

Теорема Дезарга и недоступные точки схода. Случается, что при построении перспективного изображения художник, а еще чаще архитектор сталкиваются с такой трудностью: точка схода некоторой линии оказывается за пределами картины (чертежа). Покажем, как теорема Дезарга может помочь в этом случае.

Пусть на плоскости картины К даны две прямые а и b, идущие в недоступную точку схода (в качестве одной из таких прямых чаще всего выступает линия горизонта). Требуется через некоторую точку С∈К провести прямую с в недоступную точку схода. Выберем на плоскости К произвольную точку L и проведем через эту точку три произвольных луча l₁, l₂, l₃. Лучи l₁, и l₃ пересекут прямые а и b в точках А, В и А', В' соответственно. Через точку С проведем прямые МА и СВ, пересекающие луч l₂ в точках М и N. Наконец, проведем прямые МА' и NB' до пересечения в точке С'. Как следует из теоремы Дезарга, прямая с, проходящая через точки С и С', пересекается с прямыми а и b в одной точке, т. е. прямая с и является искомой прямой, идущей в недоступную точку схода.

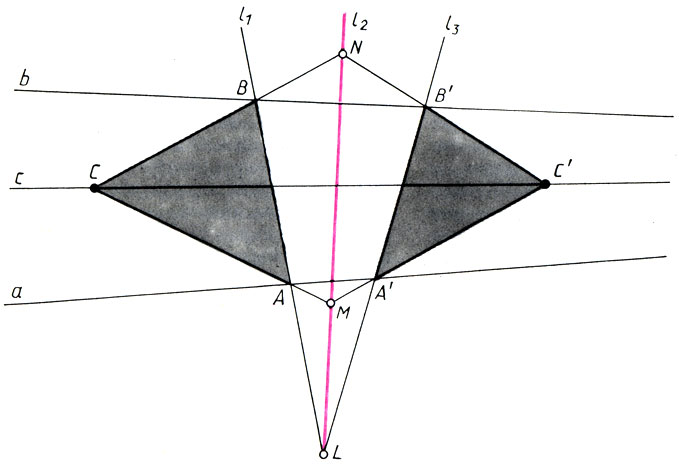
Проведение прямой с в недоступную точку схода с помощью теоремы Дезарга

Мы познакомились с геометрическими методами отображения трехмерного пространства на плоскость картины. Методы эти составляют предмет изучения самостоятельной науки - начертательной геометрии, которая в свою очередь стимулировала развитие еще одной ветви математики - проективной геометрии. Но эти же геометрические методы живут полнокровной жизнью и в искусстве живописи. Они помогают художнику разрешать извечный парадокс искусства живописи: заставить зрителя в плоском холсте, покрытом красками, увидеть реальный трехмерный мир, окружающий человека. В разные эпохи эта "вечная" проблема живописи решалась по-разному, в том числе и разными геометрическими методами, в чем легко убедиться, прочитав следующую главу.