20. Перспектива - геометрия живописи [1992 Волошинов А.В.

Все проблемы Перспективы можно пояснить при помощи пяти терминов Математики: точка, линия, угол, поверхность и тело.

В первом наскальном изображении первый первобытный художник столкнулся с непростой математической задачей: отобразить трехмерный оригинал на двумерную плоскость "картины". Сама природа помогла ему в решении этой задачи, ибо, как заметил Леонардо да Винчи, "первая картина состояла из одной-единственной линии, которая окружала тень человека, отброшенную солнцем на стену".

Почему художник не довольствовался трехмерной скульптурой, а стремился к двумерному изображению оригинала, понять нетрудно: плоская поверхность пещеры или стены храма, глиняной таблички или папируса, пергамена или бумаги была удобным носителем графической информации. В последних случаях такую поверхность можно было попросту свернуть в рулон и унести с собой.

Люди издревле научились отображать всевозможные объекты окружающего их трехмерного мира на двумерную плоскость картины. Однако по мере развития такого искусства отображения все чаще возникал вопрос: насколько точно и насколько убедительно эти плоские образы отражают реальные трехмерные прообразы? На эти вопросы призвана была ответить наука, и прежде всего геометрия. И она по мере сил отвечала на них, хотя решение столь простой на первый взгляд задачи растянулось на тысячелетия.

В этой главе мы рассмотрим с точки зрения геометрии, какие основные возможности имеются в решении задачи отображения трехмерного пространства на двумерную плоскость. А в главе 22 мы увидим, как эти возможности реализовы-вались в искусстве живописи.

Раздел геометрии, в котором изучаются различные методы изображения пространственных форм на плоскости, называется начертательной геометрией. В основе начертательной геометрии лежит метод проекций, сущность которого такова. В пространстве выбирают фиксированную точку S - центр проектирования и плоскость проекций К (картинную плоскость), не проходящую через S. Для получения изображения - проекции^* - объекта на плоскость К через центр проекций S и каждую точку А, В, С,... объекта проводят проектирующие лучи до пересечения с плоскостью К. Совокупность точек пересечения проектирующих лучей с картинной плоскостью и даст изображение (проекцию) объекта, которое называют центральной проекцией.

Представим теперь, что центр проектирования S уходит в бесконечность. Тогда проектирующие лучи становятся параллельными между собой. Считая центр проектирования расположенным в бесконечно удаленной точке S_∞ , мы, таким образом, приходим к важному частному случаю центрального проектирования - параллельному проектированию. Наконец, важным частным случаем параллельных проекций являются ортогональные проекции, когда проектирующие лучи ортогональны К, т. е. образуют прямые углы с плоскостью проекций К.

При построении проекций некоторые свойства оригинала сохраняются и на его проекции. Такими неизменными свойствами - инвариантами - при центральном проектировании обладают:

При параллельном проектировании помимо того сохраняются следующие свойства:

6) метрические свойства плоских фигур, параллельных картинной плоскости (плоские фигуры, параллельные картинной плоскости, проектируются на эту плоскость без искажений).

Обратим внимание на то, что свойство параллельности прямых при центральном проектировании не сохраняется.

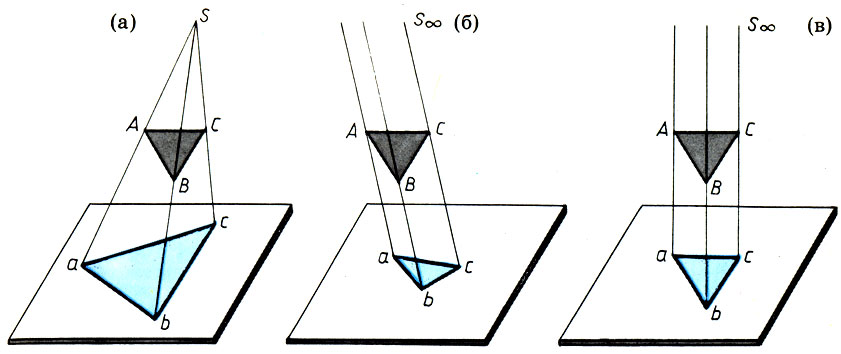
Важнейшие виды проекций: центральные (а), параллельные (б) и ортогональные (в)

Приложение начертательной геометрии к технике выдвинуло требование "обратимости" чертежа, т. е. возможности точного определения пространственной фигуры по плоскому чертежу, или, говоря языком математики, взаимно однозначности отображения пространства на плоскость. Рассмотренные проекции являются однозначными, но не взаимно однозначными отображениями, т. е. каждой точке пространства соответствует единственная точка плоскости, но не наоборот. Нетрудно убедиться и в том, что для определения положения точки в пространстве по ее чертежу необходимо иметь две проекции точки, полученные из двух центров или при двух направлениях проектирования. Эта гениально простая мысль и составляет основу начертательной геометрии, заложенную выдающимся французским математиком, активным деятелем Великой французской революции, другом и советником Наполеона Гаспаром Монжем (1746-1818).

Суть метода Монжа можно изложить двумя предложениями, как это сделал член-корреспондент АН СССР Б. Н. Делоне: "Пространственный объект проектируется ортогонально (т. е. перпендикулярами) на плоскость и также проектируется на некоторую другую ей перпендикулярную плоскость, и затем одна из этих плоскостей поворачивается вокруг прямой пересечения этих плоскостей, пока не совместится с другой. В результате на одной и той же плоскости оказываются две различные проекции (вида) рассматриваемого объекта, по которым уже можно, методами Монжа, восстановить размеры, углы и т. д., имеющиеся у данного пространственного объекта в натуре."

Несмотря на то что ортогональные проекции известны человечеству с незапамятных времен (вся живопись Древнего Египта есть не что иное, как ортогональные проекции на плоскость рисунка), простая мысль использовать две ортогональные проекции для получения взаимно однозначного отображения пространства на плоскость пришла Монжу лишь в конце XVIII века. Имея огромное практическое значение в теории фортификации, метод Монжа еще в течение 15 лет оберегался как военная тайна. Простота метода Монжа ошеломила современников. Познакомившись с его идеями, Лагранж, перемежая иронию с восторгом, воскликнул: "До слушания лекции Монжа я не знал, что мне известна начертательная геометрия!"

На рисунке показаны различные типы проекции одного и того же прямоугольного параллелепипеда с отношением сторон 1:2:3. Метод ортогональных проекций Монжа иллюстрирует рисунок а. Заметим, что третья проекция с точки зрения математики является лишней, но ею часто пользуются, чтобы создать более полное представление о пространственном теле. Как отмечалось, при ортогональном проектировании сохраняются истинные размеры контуров тела.

Однако ортогональные проекции не дают целостного впечатления о форме пространственного объекта. Более наглядное представление о форме тела дают аксонометрические проекции^* - частный вид параллельных проекций, отображающих на плоскость К все точки пространственного объекта вместе с декартовой системой координат, к которой этот объект отнесен. На рисунке б построена аксонометрическая проекция нашего параллелепипеда. Мы видим, что в аксонометрии происходят искажения линейных размеров, различные по разным осям. Согласно основной теореме аксонометрии - теореме Польке, три произвольных отрезка на плоскости, выходящие из одной точки, могут быть приняты за параллельную проекцию трех равных и взаимно перпендикулярных отрезков, выходящих из некоторой точки пространства, Следовательно, аксонометрические оси и коэффициенты искажения по ним (отношение длины по аксонометрической оси к истинной длине по соответствующей оси) могут быть выбраны произвольно. (В нашей аксонометрии углы между осями равны 120°, а коэффициенты искажения - 1.)

^* (Аксонометрия - от греч. axon - ось и metreо - измеряю.)

Наконец, на рисунке в построена центральная проекция нашего параллелепипеда. Сопоставляя все три проекции, мы видим, что перспектива наиболее адекватно, т. е. "похоже", передает видимый нами объект. Это замечательное свойство центральной проекции и снискало ей славу в искусстве живописи, где она получила особое название - перспектива (от лат. perspicio - ясно вижу). Перспективные проекции, являются и наиболее трудными из рассмотренных нами, поэтому остановимся на перспективе более подробно.

Прежде всего заметим, что реально существующий мир и видимый нами мир - не одно и то же. В самом деле, вспомним всем хорошо знакомый пример: рельсы железной дороги кажутся нам сходящимися на горизонте, хотя мы прекрасно знаем, что это не так и ни один машинист, увидев такую картину, не бросится останавливать поезд.

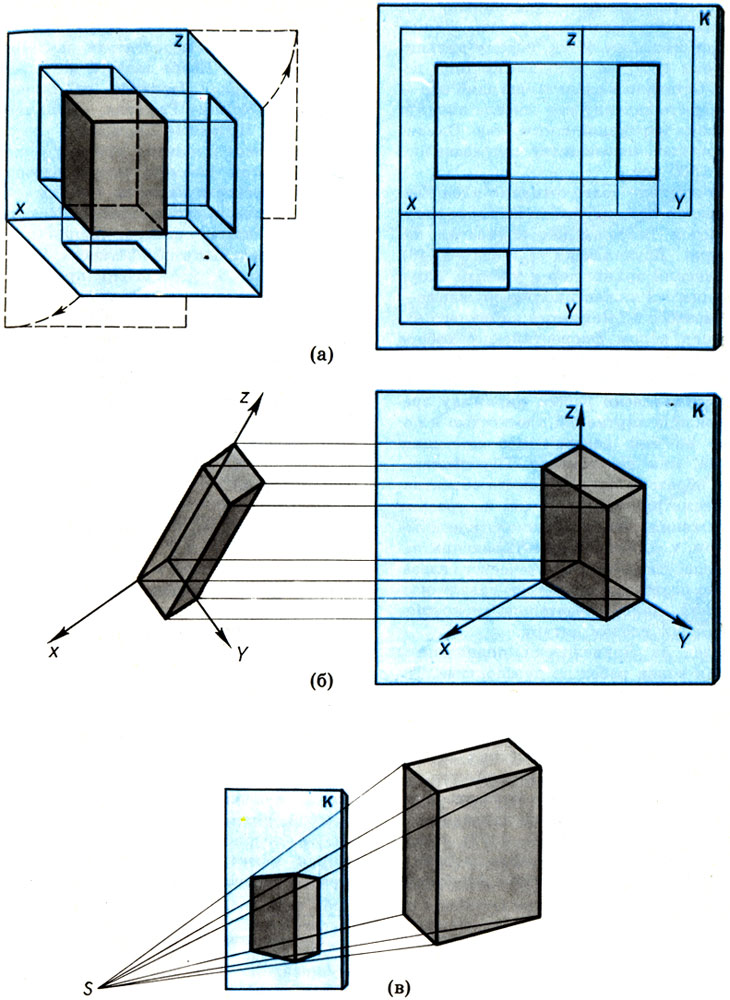
Ортогональные (а), аксонометрические (б) и центральные проекции (в) прямоугольного параллелепипеда с отношением сторон 1:2:3

Объяснение этому "парадоксу" было известно еще до нашей эры. В своем сочинении "Оптика" Евклид постулировал, что мы воспринимаем предметы, когда исходящие от них прямолинейные лучи света сходятся в нашем глазу. Таким образом, всю систему лучей зрения можно представить в виде "пирамиды зрения", вершина которой находится в глазу, а основанием служит рассматриваемый объект. В предложении 4 "Оптики" Евклид доказал, что из двух предметов одинакового размера более удаленный, т. е. видимый под меньшим углом зрения, кажется меньшим. Итак, почему дальние предметы кажутся меньшими, было понятно. Оставалось сделать еще один шаг - рассмотреть картину как сечение пирамиды зрения картинной плоскостью. Однако на этот шаг человечеству потребовалось более 1500 лет.

Мучительно долго ожидали идеи Евклида своего часа, и только в XIV веке могучий поток Возрождения подхватил их. Филиппо Брунеллёски (1377-1446), итальянский архитектор и ученый, автор выдающегося инженерного сооружения - грандиозного 42-метрового каменного купола над хором флорентийского собора Санта-Мария дель Фьоре, ставшего символом Флоренции,- сделал оставшийся шаг. Брунеллёски рассек пирамиду зрения Евклида картинной плоскостью и получил на ней центральную проекцию объекта, или перспективу. Перспектива, таким образом, была не просто объективным геометрическим методом построения изображения, но и "физиологическим" методом, т. е. методом, учитывающим закономерности работы человеческого глаза. Именно поэтому перспектива давала изображения, столь замечательно "похожие" на видимую глазом натуру.

Вслед за Брунеллёски поднимается мощная волна работ по перспективе. Титаны Возрождения не замыкаются в геометрических построениях, а воплощают теоретические разработки в своих бессмертных полотнах. Геометрия и живопись идут рука об руку. Вместе с трактатами "О живописи" Леона Баттисты Альберти, "О живописной перспективе" Пьеро делла Франчески^* (ок. 1420-1492), "Трактатом о перспективе" Леонардо да Винчи, "Руководством к измерению" Альбрехта Дюрера, "Шестью книгами о перспективе" Гвидо Убальди (1545-1607) рождаются и такие памятники перспективе, как "Бичевание Христа" Пьеро делла Франчески, "Тайная вечеря" Леонардо да Винчи, "Обручение Марии" Рафаэля, "Меланхолия" и "Св. Иероним" Дюрера...

^* (Пьеро делла Франческа был не только живописцем, но и математиком, автором "Книги о пяти правильных телах", учителем Луки Пачоли. )

Но вернемся к нашему примеру с железной дорогой. Посмотрим, как изобразятся на плоскости картины "рельсы" - прямые, ортогональные плоскости картины, и "шпалы"- равноотстоящие прямые, параллельные этой плоскости. Пусть точка зрения S есть центр проекций, который определяет положение глаза художника; Т - горизонтальная плоскость, на которой лежат изображаемые объекты; К - плоскость картины (К1.Т). Из точки S мы смотрим^* на "точки закрепления рельс к шпалам" А₁, А₂, А₃, ... и В₁, В₂, В₃,... Точки пересечения лучей зрения SA_i и SB_i с плоскостью К дают нам изображения (проекции) этих точек а₁, а₂, а₃,... и b₁, b₂, b₃,... на картине К. Очевидно, что точки, лежащие в основании картины, tt - линии пересечения плоскостей К и Т - при проектировании переходят сами в себя, т. е. линейные размеры в основании картины не искажаются.

^* (Следует отметить, что теория перспективы - это наука о видении одним глазом (монокулярная теория). Бинокулярная теория зрения пока далека от завершения.)

Ясно, что по мере удаления точек А_i и B_i в бесконечность лучи SA_i и SB_i становятся все более пологими и все ближе подходят друг к другу (так как угол зрения, под которым мы видим равные отрезки A_iB_i, уменьшается), пока наконец не сольются, заняв предельное положение SS_∞. Можно считать, что луч SS_∞пересекается с обоими "рельсами" (и вообще, с любой прямой, параллельной "рельсам") в бесконечно удаленной точке Sx, которая проектируется в главную точку картины О. Точка О лежит на прямой hh, называемой линией горизонта, которая есть линия пересечения картинной плоскости К и плоскости, проходящей через точку S параллельно плоскости Т. Расстояние SS' = 00' называется высотой точки зрения.

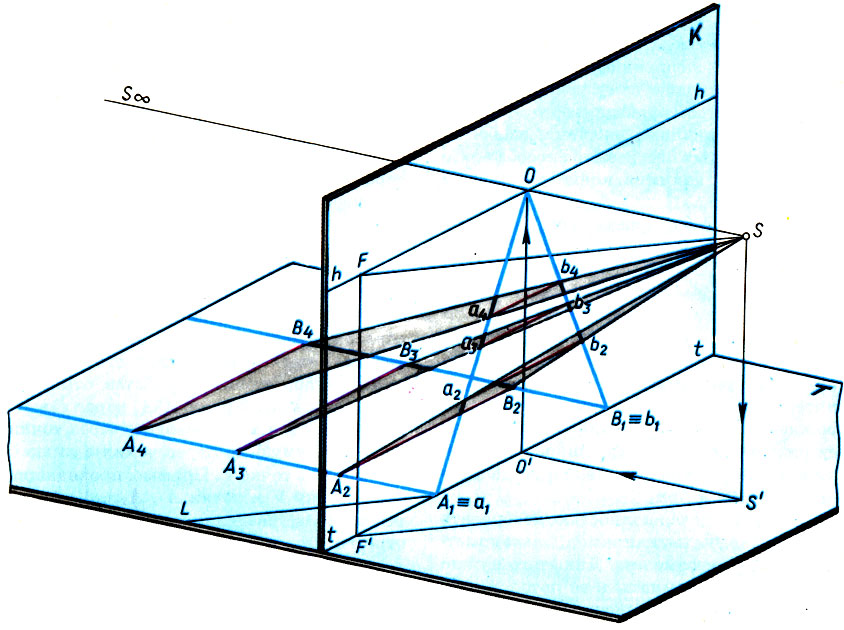
Построение перспективного изображения прямых, перпендикулярных и параллельных картинной плоскости

Таким образом, мы приходим к основной теореме теории перспективы: семейство бесконечных параллельных прямых на плоскости Т, не параллельных основанию картины, изображается семейством пересекающихся отрезков на плоскости К, причем точка пересечения этих отрезков - точка схода - лежит на линии горизонта hh. Различным направлениям на плоскости Т соответствуют различные точки схода на линии горизонта. Следовательно, линия горизонта есть геометрическое место точек схода для всевозможных направлений на плоскости Т. Прямые плоскости T, параллельные основанию картины, точки схода не имеют и проектируются на плоскости К в прямые, параллельные основанию картины ("шпалы" на рисунке).

Разумеется, получать проекции точек объекта на картинной плоскости с помощью пространственных построений, как это сделано на рисунке, трудно и неудобно. Поэтому еще архитекторами Возрождения был разработан способ построения перспективы, названный способом архитекторов, позволяющий с помощью точек схода и линии горизонта непосредственно переходить с горизонтальной плоскости Т на плоскость картины К. Для построения точки схода F линии L по способу архитекторов из проекции точки зрения S' проводят линию L' параллельно L до пересечения с основанием картины в точке F'. Точка F' есть проекция точки схода F на основание картины. Восстанавливая из F' перпендикуляр до линии горизонта, находим саму точку схода F. (Доказательство справедливости этого построения очевидно из рисунка, а обоснование остальных построений способа архитекторов мы дадим в конце следующей главы.)

Перспектива открыла перед живописцами небывалые возможности. Впервые у художников появился геометрический метод изображения не отдельного предмета, а всего видимого трехмерного пространства, всего окружающего мира. Невиданные возможности перспективы наиболее ярко раскрывались в изображении интерьера. Вот почему художники Возрождения так любили изображать интерьер (вспомним "Афинскую школу" Рафаэля и "Тайную вечерю" Леонардо да Винчи, см. с. 55 и 308).

В самом деле, полностью изобразить интерьер комнаты, например, в аксонометрии просто невозможно. Для этого нужно считать стены комнаты и ее потолок прозрачными. Можно, конечно, дать ортогональные проекции стен, пола и потолка, но это будет чертеж комнаты. Иное дело - перспектива. Она чудесным образом раскрывает перед нами всю комнату, позволяя увидеть одновременно и ее стены, и пол, и потолок.

На рисунке в способом архитекторов построена перспектива "математической" комнаты в форме куба, имеющей окно, дверь, две балки на потолке и пол, выложенный квадратными плитами. Вынутая стена ABCD комнаты совпадает с плоскостью картины К и передается на ней без искажений (естественно, сохраняются и все размеры на ABCD, такие, как х, у, z и т. д.). Глаз художника расположен напротив центра комнаты, т. е. главная точка картины находится в центре квадрата ABCD. В главной точке картины пересекаются все прямые, перпендикулярные плоскости картины. Для построения перспективы берем план пола комнаты и, проводя из проекции точки зрения S' прямые, параллельные диагоналям пола, находим проекции точек схода F₁' и F₂' диагоналей. Перенося эти точки на линию горизонта hh, получаем точки схода диагоналей F₁ и F₂. В этих точках на перспективе пересекаются диагонали пола и параллельные им (на плане) прямые. Дальнейшее построение перспективы пола и стен комнаты, а также горизонтальных границ окна и двери понятно из рисунка.

Разметка вертикальных линий окна точками А₂, А₃, А₄ делается следующим образом. Берем отрезок A₁A₅, задающий вертикальные линии окна, и его перспективное изображение а₁а₅. Затем откладываем из точки а₁ отрезок A₁A₅ параллельно линии горизонта и проводим через точки А5 и а₅ прямую до пересечения с линией горизонта в точке V. Прямые, проходящие через точку V и точки А₁, А₂, ... , А₅ отрезка A₁A₅, разделят перспективу этого отрезка а₁a₅ в том же отношении. Аналогично размечаются вертикальные линии двери. Перспектива нашей "математической" комнаты готова.

Заметим, что проблема правильного построения перспективы "клетчатого" пола долго не давалась художникам Возрождения. Вот почему, решив эту геометрическую задачу, мастера Возрождения так любили изображать квадраты пола на своих полотнах (см. например, "Афинскую школу" и "Обручение Марии" Рафаэля, с. 310). Квадратные плиты были своеобразной координатной сеткой на плоскости пола и придавали глубине картины особую выразительность.

Заканчивая короткое знакомство с геометрическими основами теории перспективы, покажем, как построить перспективу прямоугольного параллелепипеда, расположенного под углом к плоскости картины К. Для простоты будем считать, что переднее ребро параллелепипеда лежит в плоскости картины. Пространственные построения здесь неудобны (см. рисунок в на с. 277), поэтому перспективу параллелепипеда найдем способом архитекторов, используя только основание параллелепипеда - прямоугольник ABCD, лежащий в горизонтальной плоскости Т.

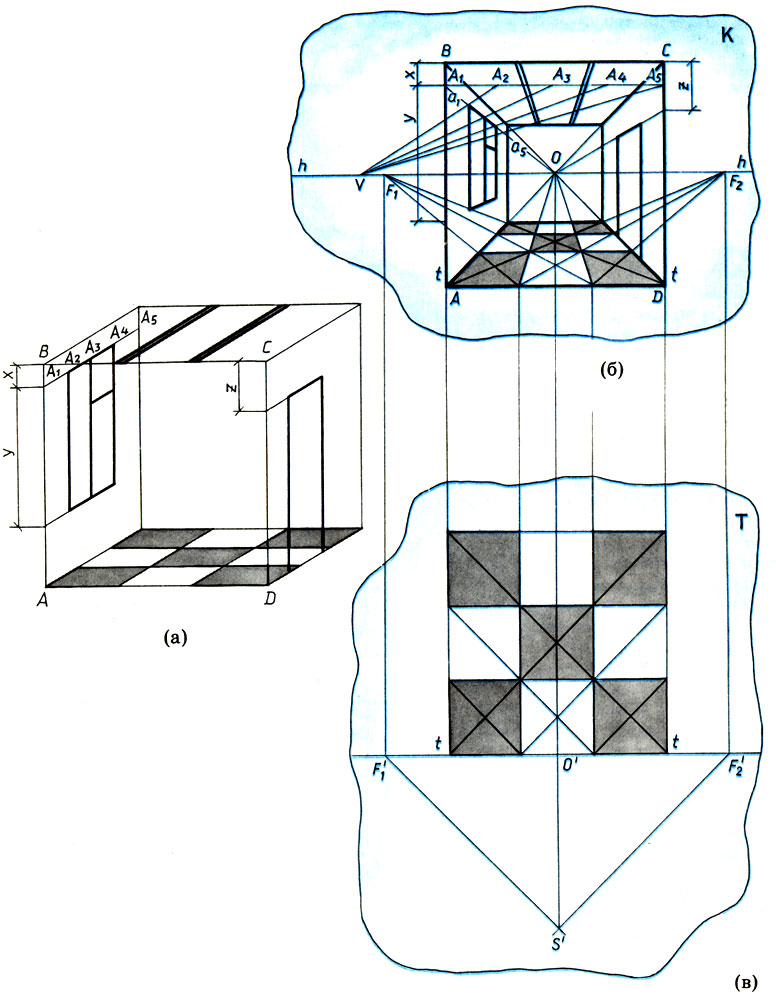
Построение перспективы интерьера комнаты способом архитекторов: (а) - аксонометрия комнаты; (б) - перспектива комнаты; (в) - план пола комнаты и проекция точки зрения

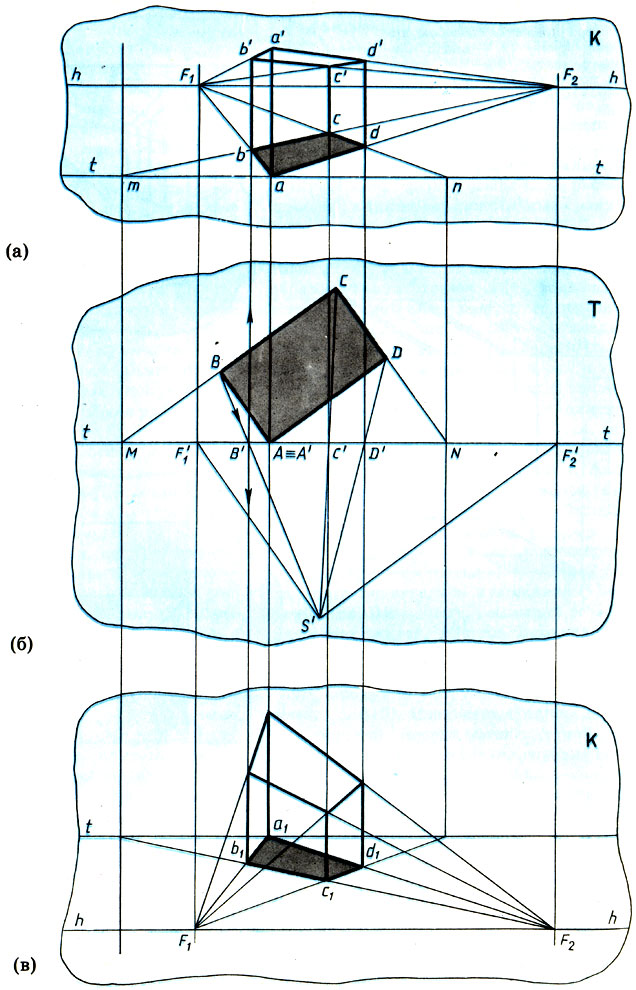
Прямая (а) и обратная (в) перспективы прямоугольного параллелепипеда, расположенного под углом к картинной плоскости (б)

Прежде всего на плоскости картины К проводим линию основания tt и линию горизонта hh, которая выбирается по усмотрению художника (это высота точки зрения художника). Затем, проводя прямые S'F₁' и S'F₂' параллельные CD и СВ, строим точки схода F₁ и F₂ этих линий. Делая построения, понятные из рисунков а, б, получаем перспективу abcd основания ABCD. Далее, восставляя из точек а, b, с, d перпендикуляры и откладывая из точки а высоту параллелепипеда (так как переднее ребро параллелепипеда лежит в плоскости картины, то его размеры в перспективе сохраняются), получаем вершину параллелепипеда а'. Наконец, соединяя точку а' с точками схода F₁ и F₂, а также соединяя образуемые при этом точки b' и d' с соответствующими точками схода, получаем перспективу всего параллелепипеда.

Вообразим теперь, что, проводя линию горизонта hh, мы ошиблись и она оказалась у нас не выше, а ниже основания картины (рис. в на с. 282). В точности повторяя все предыдущие построения, мы получим обратную перспективу а, b, с, d прямоугольника ABCD.

Вместо привычного в прямой перспективе сокращения видимых размеров предмета по мере удаления его от наблюдателя в обратной перспективе происходит увеличение этих размеров. Заметим, что обратную перспективу a₁b₁c₁d₁ прямоугольника ABCD можно увидеть, если посмотреть на прямую перспективу abed этого прямоугольника из-за картины, да еще и "вверх ногами" (в этом легко убедиться, перевернув книгу и посмотрев на abed на свет с другой стороны страницы).

Если далее повторить все те же построения с высотами параллелепипеда, по-прежнему сохраняя его высоту в плоскости картины, то мы получим обратную перспективу всего параллелепипеда. Еще раз обратим внимание на "странность" обратной перспективы: видимые размеры фигуры в обратной перспективе по мере удаления от глаза наблюдателя не сокращаются (как в прямой перспективе), а увеличиваются.

До тех пор пока ваши построения обратной перспективы носили чисто геометрический характер, в них, может быть, и не было бы ничего странного, кроме замеченного расхождения обратной перспективы с нашим зрительным опытом. Но уж совсем удивительным оказывается то, что именно обратная перспектива является геометрической основой древнерусской живописи. Такая странная геометрия живописи Древней Руси до сих пор не дает покоя ее исследователям. Некоторые называют ее просто "ошибочным приемом". Другие связывают "потустороннее" геометрическое происхождение обратной перспективы (вспомните наш взгляд из-за картины) с тем "потусторонним" неземным ирреальным миром, который призвана была изображать древнерусская икона. Наконец, есть и третий, как нам кажется, наиболее реалистичный и научный взгляд на обратную перспективу. Но обо всем этом речь пойдет несколько позже.

Итак, перспектива - это очень просто. Это чистая геометрия. Так что же, овладев геометрией перспективы, каждый может стать художником? К сожалению, нет. Математически точная перспектива - это еще не живопись, а только чертеж, хотя бы и такой прекрасный, как воспроизведенный здесь нами. Перспектива - это только геометрическая основа живописи. Но эта основа мертва, до тех пор пока художник не вложит в нее частичку своей души, не сделает ее живописью. При этом в чем-то можно и поступиться геометрией (что часто и делали художники) во имя жизни самого искусства живописи.

Как мы видели, построение перспективных изображений - дело довольно сложное. Поэтому наряду с разработкой строгих математических основ теории перспективы художники Возрождения старались дать своим собратьям и простые практические методы построения перспективы. Остроумное устройство для построения перспективы описывает А. Дюрер в трактате "Руководство к измерению". На стене закреплена проушина (это "глаз" художника), через которую продет шнур, идущий последовательно от точки к точке предмета (это "луч зрения"). Шнур проходит через раму, которая закрывается дверцей с натянутой на ней бумагой. Рама имеет подвижные нити - горизонтальную и вертикальную, позволяющие фиксировать координаты точки пересечения "луча зрения" с открытой рамой и переносить их на бумагу (для этого шнур убирают, закрывают дверцу с бумагой и отмечают на ней соответствующую точку). Свой метод Дюрер иллюстрирует прекрасной гравюрой, которая, несмотря на свое "техническое" содержание, сама является произведением искусства.

Перспективный чертеж церкви Покрова Богородицы на Нерли - геометрия, переходящая JB искусство

Как происходило дальнейшее развитие теории перспективы? Уже наше короткое знакомство с перспективой убеждает в том, что по перспективному изображению весьма трудно судить об истинных размерах предмета. Желая преодолеть эту трудность, математик и архитектор из Лиона Жерар Дезарг (1593-1662) в работе "Общий метод изображения предметов в перспективе" предложил использовать при построении перспективы метод координат. Изображение предмета предлагалось выполнять совместно с системой координат, относительно которой он ориентирован в пространстве. Метод Дезарга положил начало новому самостоятельному методу изображения, впоследствии названному аксонометрическим.

Дезарг обратил внимание и на другую особенность, возникающую при построении перспективы. Как мы видели, при центральном проектировании прямые, параллельные в горизонтальной плоскости Т, могут переходить в пересекающиеся прямые в картинной плоскости К (см. на с. 281). При этом точка схода параллельных прямых в картинной плоскости (точка О на рисунке) не имеет своего прообраза в плоскости Т. Желая избавиться от тацой особенности, Дезарг предложил дополнить обычную евклидову плоскость (плоскость с конечными точками) бесконечно удаленными точками, названными несобственными точками. Сколько бесконечно удаленных точек следовало ввести на плоскости Т? Очевидно, сколько есть направлений для параллельных прямых, так как естественно считать, что все параллельные друг другу прямые пересекаются в одной бесконечно удаленной точке. Ясно, что таких точек бесконечно много. Совокупность бесконечно удаленных точек на плоскости Т образует бесконечно удаленную прямую, которая на картинной плоскости К переходит в линию горизонта. Плоскость, дополненная бесконечно удаленными точками и бесконечно удаленной прямой, получила название расширенной, или проективной плоскости.

Далее Дезарг предложил стереть различия между собственными и несобственными элементами расширенной плоскости. Это значительно упрощало и обобщало многие рассуждения. В самом деле, в таком случае на расширенной плоскости исчезало само понятие параллельности прямых, так как параллельные прямые можно было считать пересекающимися в бесконечно удаленной точке. Но тогда автоматически устранялась и та особенность центрального проектирования, с которой все и началось: на расширенной плоскости пересекающиеся прямые (в том числе и пересекающиеся в несобственной точке, т. е. параллельные) проектировались в пересекающиеся. Таким образом, на расширенной плоскости центральные проекции дополнялись еще одним инвариантом (см. с. 275) - свойством прямых пересекаться.

Дюрер. Устройство для изображения предметов в перспективе. Гравюра. Ок. 1520

Поведение точек и прямых на расширенной плоскости управлялось лишь двумя аксиомами:

1) две различные точки на расширенной плоскости определяют прямую, и притом только одну, которой они принадлежат;

2) две различные прямые на расширенной плоскости определяют точку, и притом только одну, через которую они проходят.

Нет параллельных прямых! Нет знаменитого пятого постулата Евклида, который 2000 лет не давал покоя математикам! Геометрия расширенной плоскости - это геометрия точек, прямых и пересечений. Любая теорема о конфигурации этих элементов на расширенной плоскости оставалась справедливой и для любой центральной проекции этой конфигурации. Отсюда и пошло название новой геометрии - проективная геометрия.

Так, в недрах искусства живописи родилась новая наука - проективная геометрия - еще одно свидетельство тесных уз между наукой и искусством.

Новые идеи оказались чрезвычайно плодотворными и позволили Дезаргу получить ряд первоклассных результатов, в том числе и знаменитую теорему, носящую его имя. Однако идеи Дезарга опередили его время. Его сочинения отпугивали современников сжатостью изложения и многочисленностью новых обозначений. О Дезарге и его методе просто забыли...

Пути науки неисповедимы. Судьбе угодно было распорядиться так, чтобы ровно через 150 лет после смерти Дезарга его идеи возродил его же соотечественник. Однако произошло это не в родной Франции, а в далекой России, в глухом провинциальном городе Саратове...