19. "Законы красоты" человека

Человек - мера всех вещей.

Протагор

Во все времена, от наскальной живописи в Сахаре до полотен Сальвадора Дали, человек был и остается главной темой изобразительного искусства. "Виллендорфская Венера" или Венера Милосская, царь Хаммурапи или бог Аполлон, Сикстинская мадонна или девушка с персиками - для художника все они прежде всего были образами человека. Более того, в предыдущей части мы увидели, что образ человека, его пропорции нашли воплощение и в архитектурных произведениях от античных й древнерусских храмов до ультрасовременных сооружений Ле Корбюзье. Настало время подробнее поговорить об этих пропорциях - "законах красоты" человека^*.

^*(Конечно, каковы они, "законы красоты" человека, никто не знает; поэтому речь в этой главе пойдет лишь о пропорциях человека, которые, безусловно, являются составной частью этих законов.)

С древнейших времен пропорции человека составляли предмет изучения художника, его "математическую лабораторию". На первых порах художником руководило, быть может, не столько стремление "дойти до самой сути", сколько необходимость в каких-то объективных - числовых или геометрических - формах передать свой опыт и свое мировоззрение преемникам. Так в искусстве возникали каноны.

Известны три древнеегипетских канона : первый канон эпохи Древнего царства, приписываемый Имхотепу (XXVIII в. до н. э.), слагает рост человека из 6 ступеней ноги; второй - эпохи Среднего и Нового царства (XXI-XII вв. до н. э.) разбивает каждую ступню еще на три части и таким образом составляет рост человека из 18 единиц; третий канон позднего периода^** (XI-IV вв. до н. э.) складывает рост человека из 21 части с четвертью. Текст египетских канонов не сохранился, хотя в дошедшем до нас каталоге храмовой библиотеки в Эдфу под шестым номером значится трактат "Предписание для стенной живописи и канон пропорций". Легко видеть, как с течением времени усложнялся древнеегипетский канон, хотя и на такие ничтожные для современника "уточнения" потребовалось ни много ни мало 2500 лет!

^**(Распределение канонов по периодам истории Древнего Египта весьма условно.)

Да, мерно, как воды Нила, текло время в Древнем Египте. И столь же неторопливым, статичным было египетское искусство. Более того, следование раз и навсегда принятым канонам, в том числе и художественным, неизменность всего сущего были своего рода философией древнеегипетского общества. И эта философия оцепенения мастерски воплощена древним художником в камне. Впрочем, для нас важно другое: почти за 3000 лет до н. э. изобразительное искусство подверглось математическому анализу и анализ этот был весьма объективен, коль скоро он устраивал древнеегипетских художников на протяжении тысячелетий. Только в математических закономерностях и можно было на века сохранить художественные каноны.

Вера египтян в универсальность математического знания отражена в одном из математических папирусов, который начинается словами: "Точное сложение - врата в знание всех вещей и мрачных тайн". А вера в универсальность канона доходила до того, что один и тот же канон египтяне применяли как в живописи, так и в архитектуре. Сетка квадратов, применявшаяся с равным успехом и в ваянии, и в зодчестве, была у египтян математической основой, организующей изображение. Меняться могли лишь абсолютные размеры этой сетки, само же изображение, его пропорции оставались неизменными.

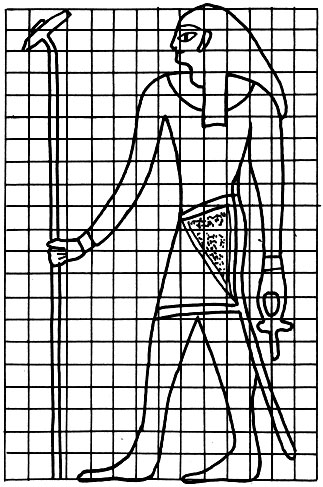
Сетка квадратов 21¹/₄ X14 - канон древнеегипетского искусства, применявшийся как в живописи, так и в зодчестве

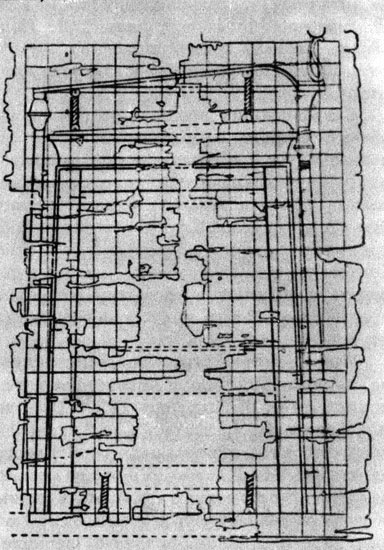
Сетка квадратов 21¹/₄X14 - канон древнеегипетского искусства, применявшийся как в живописи, так и в зодчестве

Но и внутри сетки положение фигуры строго регламентировалось математическими законами. Рассмотрим одно геометрическое построение, которое, как полагают, было известно древним египтянам. Стороны квадрата ABCD разделим в золотой пропорции точками Е_i (i = 1, 2,..., 8). (Это легко сделать, разбив данный квадрат на четыре квадрата и в каждом двойном квадрате выполнив построения, указанные на рисунке, с. 265.) Из вершины квадрата проведем в точки деления по две "диагонали". В результате образуется восьмиконечная звезда, внутри которой заключены два малых квадрата, образующих звездчатый восьмиугольник. Соединяя через одну точки пересечения малых квадратов, построим меньший квадрат со сторонами, параллельными сторонам исходного квадрата. В последнем квадрате всю процедуру можно повторить. Таким образом, получится созвездие вписанных друг в друга восьмиконечных звезд, столь же красивое, как и созвездия пятиконечных и десятиконечных звезд, которые мы наблюдали на рисунках (с. 206).

Не будем перегружать рисунок дополнительными построениями и лишать любителей математики удовольствия самим найти на чертеже две гаммы треугольников, подобных прямоугольным треугольникам АВЕ₂ и AFH. Отметим лишь, принимая сторону исходного квадрата за единицу, главное. В ΔАВЕ₂ АВ = 1, BЕ₂ = φ, АЕ₂ = √1 + φ² = ψ. В ΔABF ~ ΔАВЕ₂

AF = ¹/_ψ, BF = ^φ/_ψ, AB = 1. Из ΔABF и ΔBFG, имеющих общую сторону BF, можно найти элементы ΔBFG: BF = ^φ/_ψ, FG = ^φ/_2ψ ,BG = ^ψ/₂, а значит, и элементы ΔAFH: AF = ¹/_ψ, FH = ¹/_2ψ, АH = ^ψ/_2φ. (Напомним, что φ = (√5 - 1)/2 и при выводе соотношений в треугольниках используется аддитивное свойство ряда золотого сечения: 1 = φ + φ², φ = φ² + φ³, ... .)

Продолжая рассмотрение подобных треугольников, легко увидеть, что отношения соответствующих элементов треугольников, подобных ΔABE₂, образуют бесконечно убывающую геометрическую прогрессию :

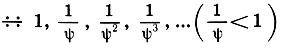(19.1)

а отношения соответствующих элементов треугольников, подобных ΔAFH, образуют прогрессию:

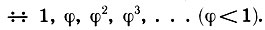(19.2)

Кроме того, имеют место комбинации двух основных типов прогрессий, а именно прогрессии вида

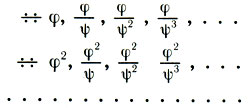(19.3)

Итак, построения рисунка дают нам не только ряд золотого сечения (19.2), но и гамму геометрических прогрессий вида

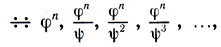(19.4)

соответствующие члены которых также находятся в золотой пропорции.

Любопытно, что в 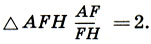Заметим также, что в

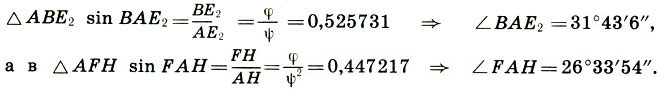
Таким образом, меньшие углы в треугольниках ΔВЕ₂ и AFH почти равны; следовательно, эти треугольники почти подобны, а углы исходного квадрата делятся "диагоналями" почти точно на три части. Итак рассмотренное построение дает нам прекрасный пример приблизительной симметрии (см. гл. 4).

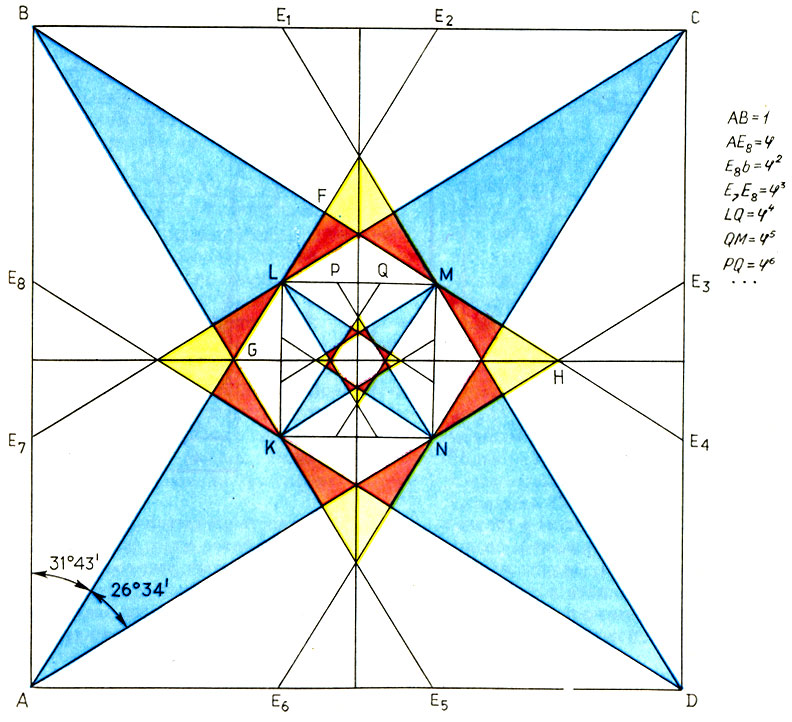
Созвездие восьмиконечных звезд, вписанных в квадрат, содержит целую гамму золотых пропорций и использовалось древнеегипетскими художниками в пропорциях человека

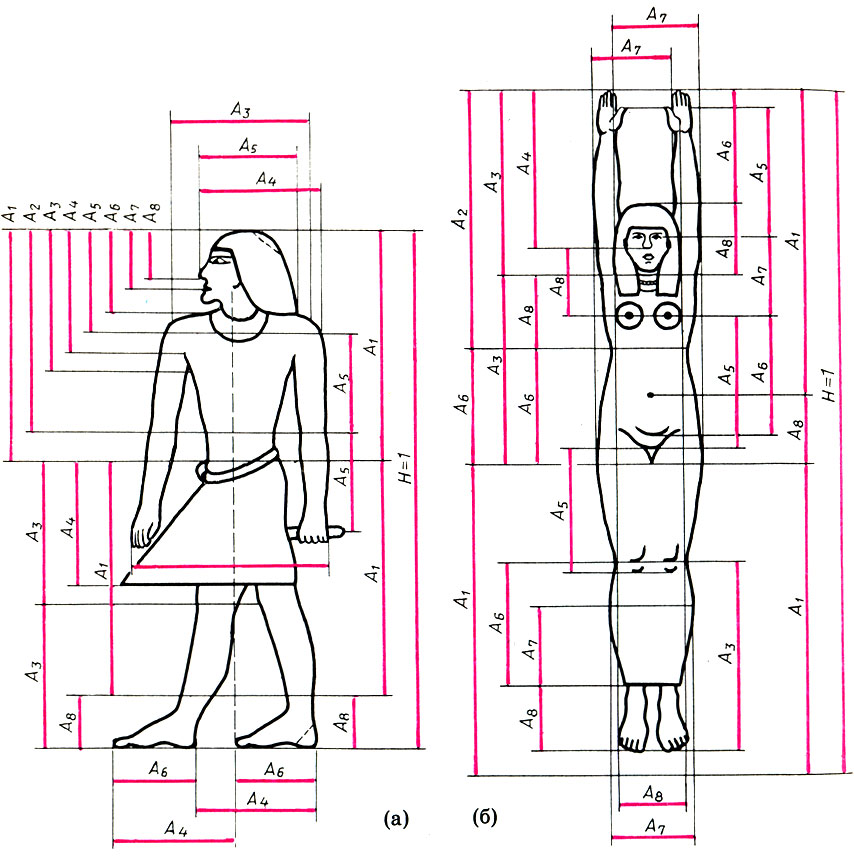
Математическое построение древнеегипетских рисунков на базе восьми пропорциональных величин (по Ф. де Кора). Фигурки жреца (а) и богини Ночи (б)

Интересно, что... Впрочем, достаточно. Оставим радость открытия любителям математики, тем более что у любителей искусства, видимо, давно уже созрел вопрос: "А какое отношение вся эта геометрия и алгебра имеют к теме нашего разговора - пропорциям человека?" А вот какое.

По мнению французского египтолога Фурнье де Кора, восемь величин из ряда (19.4), а именно

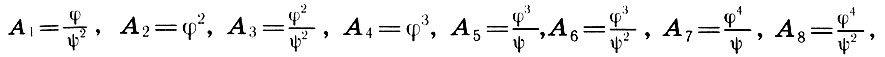(19.5)

определяют весь пропорциональный строй древнеегипетской живописи. Этот вывод де Кора основан на кропотливом изучении пропорции многих памятников изобразительного искусства Древнего Египта. На рисунке мы видим, что местоположение всех основных элементов фигур - уровень глаз, носа, рта, шеи, плеч, пояса и т. д.- с удивительной точностью определяется пропорциональными величинами (19.5), умноженными на общую длину фигурки (Н). Пользуясь (19.5) и соотношениями φⁿ = φⁿ⁺¹ + φⁿ⁺², легко доказать равенства типа 2А₁ + А₈ = 1, А₁ + А₂ + А₆ = 1, А₁ + 2А₃ = 1, А₆ + А₈ = А₃, А₃ + A₈ = A₂, А₃ + А₆ = А₁, и т. д.

Конечно, ряд (19.4) дает настолько богатую гамму пропорций, что при достаточном числе членов она может быть точнее миллиметровой линейки. Математику, разумеется, не понравится, что в (19.5) пропущены члены φ, ^φ/_ψ, ^φ2/_ψ и φ⁴ отчего теория де Кора теряет в логической стройности. Да, по прошествии четырех тысячелетий трудно установить, какой именно системой пропорций пользовался древнеегипетский художник. Поэтому так много различных теорий пропорций. Но бесспорно другое: древнеегипетский художник применял жестко детерминированную систему математических правил, которая на века определила стиль древнеегипетского изобразительного искусства. Эта математика рисунка, ставшая каноном, на века сковала искусство Древнего Египта.

Описание египетского канона позднего периода и любопытную историю, связанную с ним, мы находим у древнегреческого историка Диодора Сицилийского (ок. 90-21 гг. до н. э.). По преданию, отец Пифагора Мнесарх построил на родном острове Самос храм в честь Аполлона Пифийского, статую для которого поручили изваять прославленным греческим скульпторам. "Из древних скульпторов наибольшею славою пользовались у них Телекл и Феодор, сыновья Река, которые соорудили для самосцев статую Аполлона Пифийского. Рассказывают, что одна половина этой статуи была приготовлена Телеклом на Самосе, другая же часть была сделана его братом Феодором в Эфесе. Будучи сложенными, эти части настолько соответствовали одна другой, что казалось, будто все произведение исполнено одним мастером. Однако этот род работы никогда не применяется у греков, но большей частью употребляется у египтян... У них соразмерность статуи определяется не на глаз, но они после того, как высекут камни и обработают, разделив их на части, берут пропорцию от мельчайших до наибольших частей; рост тела они делят на 21¹/₄ - часть и так дают все соразмерности живого человека. Поэтому после того, как работники сговорятся о размерах, то, разделивши между собой труд, обрабатывают согласно заданной величине так точно, что работа их наполняет изумлением". Возможно, что эта история, рассказанная Диодором, не более чем легенда. Но важен в ней даже не факт совпадения сложенных изваяний, сколько сама постановка такого вопроса. В этой истории, даже если она и легенда, отражена безграничная вера древних греков в могущество математики, которую с равным успехом можно применять не только в инженерных расчетах (вспомним о самосском туннеле, с. 89), но и в искусстве ваяния. Создавая свои бессмертные творения, древние не боялись "алгеброй разрушить гармонию" и твердо верили: математика поможет там, где, по словам Дюрера, "рука из-за спешки обманет тебя".

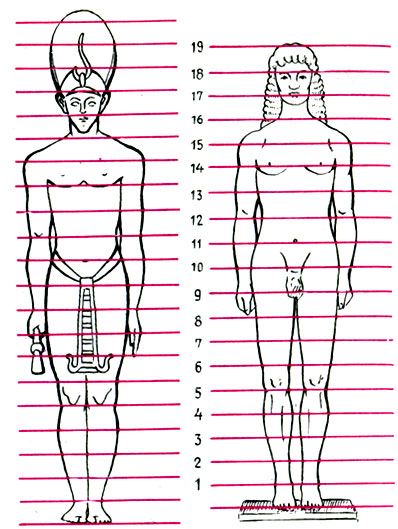
Курос из Теней ('Аполлон Тенейский'). Ок. 560 до н. э. Тождественность пропорций Аполлона Тенейского и египетского канона ваяния позднего периода еще раз доказывает факт влияния древнеегипетского искусства на раннее греческое искусство периода архаики

На рисунке изображен египетский канон, описанный у Диодора. Высота фигуры разделена точно на 21 - части, причем одно целое деление соответствует длине среднего пальца. Высота фигуры без головного убора составляет 19 частей. Рядом расположена греческая скульптура Аполлона Тенейского, относящаяся к середине VI века до н. э.- так называемому архаическому (от греч. "архайос" - древний) периоду греческого искусства. Точное совпадение пропорций этих двух фигур является математическим доказательством достаточно очевидной истины: греческое искусство периода архаики взросло на почве древнеегипетского искусства. Конечно, художественные образы этих фигур совершенно различны. Аполлон Тенейский, юноша-атлет (курос), светится жизнью и радостью: еще мгновение - и он сойдет с места навстречу новому искусству Эллады. Однако его пропорции- "математика Аполлона" - полностью сохраняют влияние древнеегипетского канона.

Греческое искусство развивалось очень динамично. Уже через 100 лет после Аполлона Тенейского, в середине V века до н. э., греческая цивилизация достигает своего апогея. Наступает период наивысшего расцвета искусства Древней Греции, именуемый периодом высокой классики. Возвышенные идеалы классики, вера в духовное, нравственное и физическое совершенство свободного эллина нашли отражение в скульптурах Поликлета, творившего во второй половине V века. Поликлет был не только гениальным скульптором, автором "Дорифора", "Дуадумена" и "Раненой амазонки", но и выдающимся теоретиком искусства.

Свои теоретические воззрения о пропорциях человека Поликлет изложил в трактате "Канон". Трактат этот, увы, не сохранился. Но как бы предчувствуя бренность написанного и бессмертие изваянного, Поликлет создает статую, в которой в бронзе воплощает свои теоретические воззрения. (Статуя эта также не сохранилась, но, к счастью, сохранилась ее римская мраморная копия.) Вот почему прославленная статуя юноши-копьеносца "Дорифор" имеет также и другое название - "Канон".

К сожалению, мы опять-таки не знаем, в каких конкретных математических отношениях выражался канон Поликлета. Но знание философских воззрений Поликлета, а главное - его скульптура помогают восстановить эти отношения. Поликлет был пифагорейцем, следовательно, он был неплохим математиком и, безусловно, был знаком с золотой пропорцией, которую пифагорейцы считали верхом совершенства. Можно только догадываться, какое изумление и радость испытал пифагореец Поликлет, когда обнаружил, что золотая пропорция присуща не только абстрактной геометрической фигуре, главному пифагорейскому символу - пятиконечной звезде, но и естественным образом входит в пропорции человека. Человеческое тело оказалось благодатным материалом для философа-пифагорейца: как нам известно, золотая пропорция пронизывает тело человека от малых размеров (три фаланги среднего пальца) до самых больших (см. с. 214). Анализ пропорций "Дорифора" и других скульптур Поликлета подтверждает наши предположения: в скульптурах Поликлета с большой точностью выдержаны пропорции ряда золотого сечения (см. с. 207)

Заметим, что в самом методе построения пропорций Поликлета есть принципиальное отличие от метода пропорционирования египтян. Египтяне исходили из какой-то условной единицы измерения, например длины среднего пальца, которую затем целое число раз "укладывали" в ту или иную часть изображения человека. Поликлет же рост человека принимает за единицу, затем фиксирует определенную часть тела, какова бы она ни была по размерам, и находит их отношение. Такое отношение могло выражаться не только отношением целых чисел, как у египтян, но и быть иррациональным числом, как в случае золотого сечения.

Таким образом, открытие золотой пропорции в строении человека, которое, по-видимому, принадлежит Поликлету, можно считать вслед за открытием закона целочисленных отношений в музыке вторым важнейшим событием в "математической теории искусств".

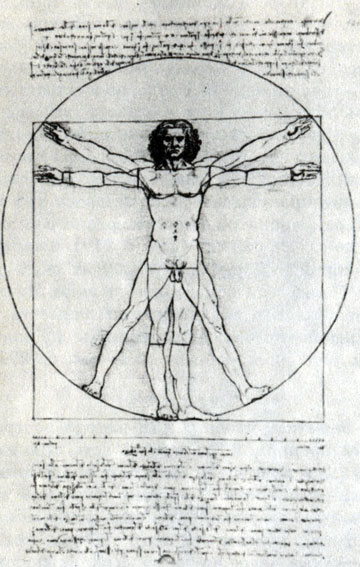
Рисунок Леонардо да Винчи из анатомических рукописей, связавший совершенные геометрические фигуры с пропорциями человека, стал своеобразным символом синтеза математики и искусства

Разумеется, в рамках этой главы невозможно даже кратко остановиться на всех теориях пропорций человека, имеющих тысячелетнюю традицию и массу вариаций. Желая ярче передать тот или иной образ, художник намеренно усиливал одни пропорции и сглаживал другие и таким образом создавал свой собственный канон. Так, уже через сто лет после Поликлета, в IV веке до н. э., в Древней Греции сложился другой, более "утонченный" канон скульптора Лисиппа, бывшего придворным художником Александра Македонского. Как писал Плиний, Лисипп изображал людей не "какими они есть", но "какими они кажутся". Впрочем, вопрос о том, какие пропорции и насколько соответствуют тому или иному художественному образу, является вопросом искусствоведения, и нам не следует погружаться в него. Однако имена двух гениальных художников и мыслителей, двух титанов эпохи Возрождения - Леонардо да Винчи и Альбрехта Дюрера - мы не можем обойти здесь молчанием.

В построении пропорций человека Леонардо да Винчи исходит прежде всего из анализа многочисленных измерений самого человека, из его анатомии, а не из каких-то "высших" соображений, как это делали средневековые художники. Жажда научного знания, основанного на опыте и только опыте, отражает переворот в мышлении эпохи Возрождения, знаменует начало экспериментального естествознания. Стремление как можно глубже изучить пропорции и вообще строение человека, столь необходимые Леонардо-художнику, переросло в страсть к науке анатомии Леонардо-ученого, Составленные им анатомические тетради явились вершиной анатомии того времени и по сей день остаются непревзойденным образцом синтеза науки и искусства.

Свои исследования Леонардо не успел (а может, и не хотел) систематизировать, и они остались рассыпанными в виде рукописных набросков, в которых говорится буквально обо всем на свете, а текст перемежается великолепными рисунками. Мы остановимся лишь на одном наиболее популярном рисунке Леонардо на тему о пропорциях. Вот отрывок текста, которым Леонардо сопровождает рисунок: "Если ты раздвинешь ноги настолько, что убавишься в росте на ¹/₁₄, и если ты тогда разведешь руки и поднимешь их так, что коснешься средними пальцами макушки головы, то должен ты знать, что центром круга, описанного концами вытянутых членов, будет пупок и что пространство между ногами образует равносторонний треугольник. А пролет распростертых рук человека равен его росту". Заметим, что идея этого рисунка восходит к известному нам сочинению Витрувия.

Свое высшее развитие учение о пропорциях человека получило в трудах Дюрера. С немецкой скрупулезностью проводит Дюрер свои измерения и в конце концов доводит разбиение человеческого тела до 1/1800 части его длины, т. е. до величины, не превышающей одного миллиметра! По мнению А. Лосева, столь тщательное измерение "стало самоцелью и каким-то измерительным спортом!". Ни до, ни после Дюрера учение о пропорциях не доводилось до такой степени точности. Но главное, пожалуй, было в другом: Дюрер отказался от создания какого-либо "идеального" канона, а разработал не менее 26 различных типов пропорций человека.

Обратимся к трактату Дюрера "Четыре книги о пропорциях". "Если я намереваюсь сделать изображение человека,- читаем мы,- то прежде всего я поступаю таким образом: я беру линейку длиннее, чем фигура, и провожу на ней прямую линию такой длины, какой должна быть изображенная фигура, так, чтобы один конец касался макушки головы, а другой подошв... И я старательно делю всю длину, которую я обозначаю цифрой 1, на части от двух до пятидесяти или ста частей, сколько мне нужно, наношу их точками на линейку возле длинной линии, провожу из них линии вверх до высоты макушки и обозначаю их цифрами 2, 3, 4 и т. д. Таким образом, меньшие цифры будут обозначать более длинные части, а большие - короткие. Так, половина всей длины будет 2, треть - 3, четверть - 4 и т. д.". Затем Дюрер указывает "важнейшие расчленяющие линии": "верхнюю я называю макушкою, следующую под нею - лбом, следующую - бровями, затем идут нос, подбородок и далее плечевые мускулы, шейная впадина, верх груди..." и так далее вплоть до подошвы.

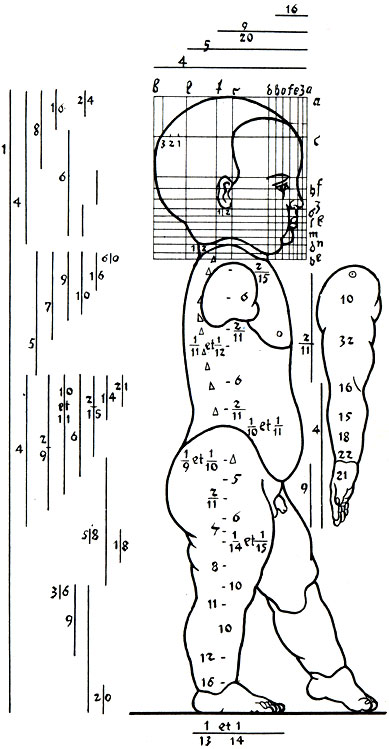
Пропорции фигурки младенца из трактата Дюрера 'Четыре книги о пропорциях'

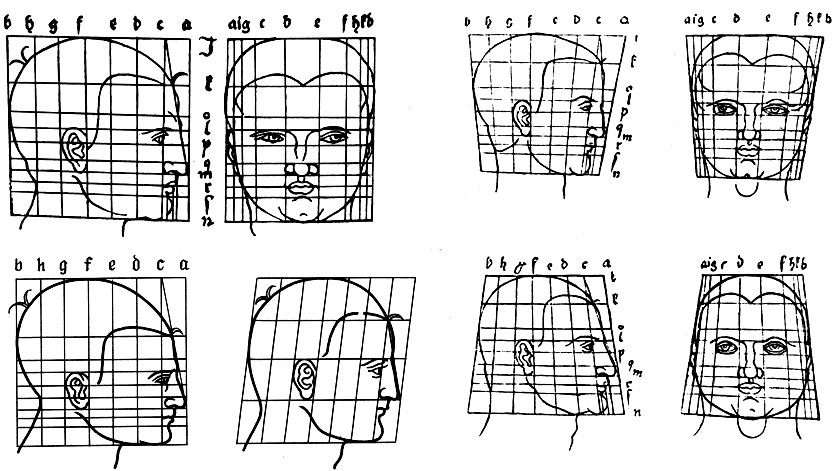
Рисунки из 'Четырех книг о пропорциях' Дюрера. В своем трактате художник пытался найти совокупность геометрических преобразований, позволяющую охватить все многообразие человеческих лиц

Хотя Дюрер и отмечает, что таковых линий "можно сделать больше или меньше", большая тщательность в анализе фигуры человека современному читателю кажется просто немыслимой. Далее следуют промеры указанных линий, которые Даются для различных типов фигур: от мужских и женских фигур до фигурки младенца. Последняя дает ясное представление о том, сколь филигранными были геометрические построения Дюрера. В третьей книге трактата Дюрер показывает, "как можно изменять или искажать эти вышеописанные размеры... благодаря чему фигура становится неузнаваемой...". Предложенный Дюрером для этой цели "измените ль" представляет собой не что иное, как систему подобных треугольников. При этом Дюрер ясно осознает, что если пропорционально изменить все размеры фигуры, то ее вид останется прежним. И напротив, "если увеличить одни части и уменьшить другие, вид вещи станет иным".

Но если пропорции человеческой фигуры еще можно как-то классифицировать, то лицо человека никак не укладывалось у Дюрера в жесткие рамки пропорциональной сетки. Дюрер изобретает массу геометрических способов, которыми можно до неузнаваемости трансформировать изображение лица. Однако чем большим становится набор таких способов, тем яснее видно, что их число уходит в бесконечность. Дюрер-художник интуитивно осознает это: в его трактате не раз проскальзывает фраза о том, что "контуры человеческой фигуры нельзя начертить при помощи циркуля и линейки". И в то же время Дюрер-геометр упрямо продолжает поиски универсального геометрического метода в построении изображения человека.

На рисунке приведены некоторые из геометрических преобразований Дюрера. В первой строке слева показано исходное "правильное" лицо. Вторая строка слева представляет собой геометрические преобразования, которые в математике называются аффинными. Аффинное преобразование, или отображение,- это такое взаимно однозначное отображение, при котором параллельные прямые исходной плоскости (верхняя строка) переходят в параллельные прямые на плоскости отображения (вторая строка). Рисунки справа дают пример более сложных геометрических преобразований.

Глядя по прошествии 500 лет на геометрические построения Дюрера, хорошо видно, как в его исследованиях назрела потребность в точной науке о непрерывных процессах, науке о проявлении прерывного в непрерывном, науке о бесконечно большом числе бесконечно малых изменений. Такая наука родилась лишь через полтора века после Дюрера в трудах Ньютона и Лейбница, когда вместе с понятием производной "в математику вошли движение и диалектика" (Ф. Энгельс, т. 20, с. 573). Таким образом, творчество Дюрера еще раз убеждает нас в том, что пути науки и искусства связаны тысячами нитей. В геометрических поисках Дюрера мы видим, как одно из величайших завоеваний человеческой мысли - дифференциальное исчисление - зрело не только в лоне науки, но и в недрах искусства.

А как развивалась теория пропорций человека после Дюрера? В XVII веке движение вошло не только в науку, но и в искусство. На смену застывшим формам объекта, где царствовали покой и пропорция, в искусстве пробуждается интерес к изменчивому, как солнечный луч, субъекту, его настроению и мироощущению. Голландским люминаристам XVII века и французским импрессионистам XIX века уже не нужны были пропорции, ибо форма, объект растворялись в их полотнах в потоках воздуха, цвета и света. Искусство XX века еще более динамично: оно разрушает все каноны, часто не успевая провозгласить свои. Сегодня каждый художник стремится создать свой собственный канон, что порождает бесконечные споры об искусстве. Тот же "канон Ильи Глазунова" расколол наших современников на сторонников и противников, что, впрочем, не мешает и тем и другим в едином строю опоясывать Манеж с выставками художника.

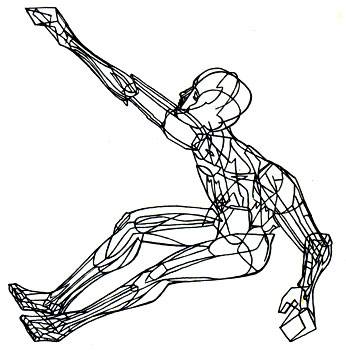
Рисунок человека, выполненный ЭВМ в исследовательском отделе фирмы 'Боинг'. Система топологических правил, введенных в ЭВМ, позволяет нарисовать различные стадии движения человека

Так что же, теория пропорций стала отжившим рудиментом искусства? Автору так не кажется. Да, в своем "арифметическом" выражении теория пропорций себя исчерпала. Да, человек - мера всех вещей - настолько разнообразен, что его нельзя втиснуть в рамки дискретных канонов. Но пропорции живы, как жив и сам человек.

Теория пропорций сегодня не умерла, а лишь замерла в ожидании качественно нового скачка, в ожидании перехода от "арифметического" к "аналитическому" и даже "компьютерному" выражению. Почва для такого скачка сегодня созрела: есть современный математический аппарат, позволяющий описать контуры человека не "на уровне циркуля и линейки"; есть современные ЭВМ с их графопостроителями и дисплеями. Нужно содружество художников и математиков.

Примеры такого содружества есть. В исследовательском отделе американской фирмы "Боинг" выполнен рисунок на ЭВМ. Рисунок математически сконструирован по стандартным дюреровским пропорциям человека и ряду топологических правил, определяющих работу суставов и обеспечивающих непрерывность контура человека при его перемещениях. Таким образом, этот "машинный человечек" может двигаться, а сама ЭВМ может создать целый мультфильм. Однако эта увлекательная тема - искусство и ЭВМ - выходит за рамки нашей книги.