
17. Пропорции: от Покрова на Нерли до Модулора ле Корбюзье
И однажды возникло из грезы, Из молящейся этой души, Как трава, как вода, как березы, Диво дивное в русской глуши.
Настало время поисков пропорций. Утверждается дух архитектуры.
В 1784 г. смиренный отец боголюбовской монашеской братии испросил разрешения у преосвященнейшего Виктора, архипастыря владимирского, благословления на разборку для монастырских потреб обветшавшей и полузаброшенной церковки. Разрешение было милостиво жаловано, но, как говорится, жизнь распорядилась по-своему: заказчики и подрядчики не сошлись в цене. Работы не начались, а там о них и вовсе забыли. Так волею судьбы остался жив памятник, который обошли стороной полчища Батыя и Мамая, пощадили столетия и пожарища бесконечных войн, шедевр древнерусского зодчества церковь Покрова Богородицы на Нерли.
В ясные летние дни среди зелени заливных лугов ее стройная белизна, отраженная гладью старицы Клязьмы, дышит поэзией сказки. Лишь в короткие минуты заката белая свеча церкви загорается тревожно-багряным пламенем. В суровые зимы бескрайняя снежная пелена, будто заботливая мать, укутывает и прячет свое замерзшее дитя. "Во всей русской поэзии, давшей миру столько непревзойденных шедевров, нет, быть может, памятника более лирического, чем церковь Покрова на Нерли, ибо этот архитектурный памятник воспринимается как поэма, запечатленная в камне. Поэма русской природы, тихой грусти и созерцания" (Л. Любимов).
Прежде чем приблизиться к тайне очарования древнерусской архитектуры, нам необходимо познакомиться с системой мер, существовавшей в Древней Руси. Мы уже отмечали (с. 198), что в разных местах земного шара, в разные времена и у разных народов эталоны длины были в принципе одинаковыми: они так или иначе происходили от человеческого тела. Эти так называемые антропометрические меры обладали ценнейшим для архитектуры качеством, о котором с введением метрической системы мер забыли, но к которому в XX веке вернулся Ле Корбюзье. Дело в том, что антропометрические меры в силу своего происхождения соразмерны человеку и поэтому удобны для конструирования искусственной среды обитания людей - архитектурных сооружений. Более того, в "человечьих" мерах заложены пропорции, отобранные самой природой, такие, как деление пополам, золотое сечение, функция золотого сечения. Следовательно, в антропометрических мерах естественным образом заложена гармония природы.
Основной строительной мерой в Древней Руси была сажень, равная размаху рук в стороны. Сажень делилась на 2 полусажени, полусажень - на 2 локтя - расстояние от кончиков пальцев до локтя, локоть - на 2 пяди - расстояние между вытянутыми в противоположные стороны большим пальцем и мизинцем. Все четко и логично. Однако чем пристальнее историки изучали древнерусские летописи, тем больше становилось саженей, а когда их число перевалило за десять, голова у историков пошла кругом. Необходимо стало навести математический порядок в древнерусской системе мер. Это сделали историк, академик Б. А. Рыбаков и архитектор И. Ш. Шевелев. Начало антропометрическим мерам дает рост человека а. Главной из всех видов саженей является мерная, или маховая, сажень См, которая равна размаху рук человека в стороны. Изучение пропорций человеческого тела показывает, что См = 1,03а. Другой важной мерой у всех народов являлся двойной шаг, который равен высоте туловища от стоп до основания шеи. Последнее расстояние, как мы знаем (с. 220), равно 5/6а. Таким образом, двойной шаг, или малая (тмутараканская) сажень, Ст = 5/6а = 0,833а. Но главный сюрприз кроется в отношении этих двух основных размеров:
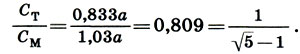 (17.1)
(17.1)Следовательно, малая сажень Ст относится к мерной См как сторона двойного квадрата к его диагонали без малой стороны:
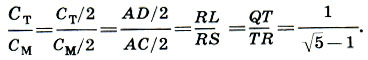
Из (17.1) ясно, что отношение мерной полусажени См/2 к малой сажени Ст равно золотому сечению:
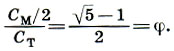 (17.2)
(17.2)Итак, в установленном самой природой отношении полуразмаха рук (RS) к высоте туловища (LQ), т. е. в отношении двух основных мер Древней Руси, заключено золотое сечение, столь распространенное в древнерусской архитектуре.
Рост человека: а = АВ
Мерная сажень: Сн = AC = CN = 1,03a
Малая (тмутараканская) сажень: 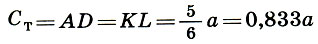
Сажень без чети: 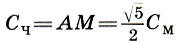
Косая новгородская сажень: 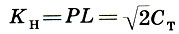
Косая великая сажень: 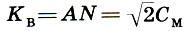
Соотношения между саженями: 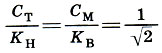
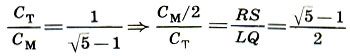
- золотое сечение
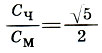
- функция золотого сечения
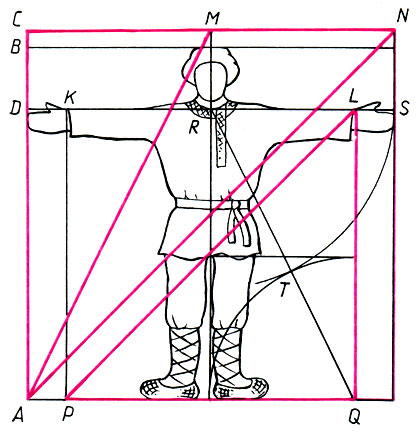
Основные древнерусские меры длины и геометрическая взаимосвязь между ними
Построив квадраты на малой Ст и мерной См саженях и проведя в них диагонали, мы получаем еще два типа саженей: косую новгородскую сажень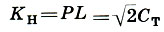 и великую косую сажень
и великую косую сажень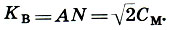 . В отличие от первых двух саженей (малой и мерной), выражающих природные меры, косые сажени получены чисто геометрическим путем. Ясно, что
. В отличие от первых двух саженей (малой и мерной), выражающих природные меры, косые сажени получены чисто геометрическим путем. Ясно, что
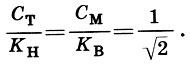 (17.3)
(17.3)
Наконец, существовала еще одна сажень, получаемая геометрическим путем. Это так называемая сажень без чети Сч, равная диагонали AM половины квадрата, построенного на мерной сажени См. У этой сажени не было соответствующей косой пары, и поэтому ее называли саженью без пары, без четы, или без чети. Из треугольника АСМ следует, что 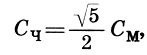 , откуда
, откуда
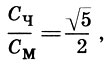 (17.4)
(17.4)т. е. отношение сажени без чети Сч к мерной сажени См равно функции золотого сечения (см. с. 219).
Таковы лишь основные типы саженей, существовавших в древнерусской метрологии. Новгородская мерная трость, найденная в 1970 г. (см. с. 219), позволила уточнить их размеры. Новгородские меры XII века соответствуют росту человека: а = 170,5 см. Тогда См = 175,6 см, Ст = 142,1 см, Кн= 200,9 см, Кв= 248,3 см, Сч= 196,3 см. Если же рост человека принять равным 6 греческим футам: а = 6*30,87 = 185,22 см, то для основных саженей (мерной и малой) получим значения: См = 190,8 см и Ст = 154,3 см. Именно эти меры наиболее часто встречаются в древнерусских храмах XI века, строительство которых, по-видимому, велось византийскими мастерами. Так, вместе с христианством Русь наследовала византийскую систему мер, которая в свою очередь взросла на античной средиземноморской культуре. Абсолютные размеры саженей в России с течением времени сильно колебались вплоть до введения метрической системы мер в 1918 г. Но важно то, что пропорциональные отношения между парными саженями сохранялись. Эти пропорции становились пропорциями архитектурных сооружений.
О том, что меры древнерусскими строителями применялись парами, свидетельствует, например, новгородская грамота XVI века, которая так описывает размеры Софийского храма в Новгороде: "а внутри главы, где окна,- 12 сажен, а от Спасова образа ото лбу до моста церковного - 15 сажен мерных". (Обмеры показывают, что упоминаемые сажени соотносятся как 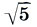 :2.) О применении парных мер говорит и новгородская мерная трость, в которой малая сажень Ст использовалась либо в паре с мерной саженью См(Ст:См = 1:(
:2.) О применении парных мер говорит и новгородская мерная трость, в которой малая сажень Ст использовалась либо в паре с мерной саженью См(Ст:См = 1:(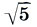 - 1)), либо с косой новгородской Кн(Ст:Кн = 1:√2). Если же на новгородской трости брались мерные полусажени в паре с малой саженью, то эта пара давала золотое сечение (См/2:Ст=φ). Итак, красота пропорций древнерусской архитектуры заложена в самой системе древнерусских мер, дающей такие важнейшие пропорции, как золотое сечение, функция золотого сечения, отношение двойного квадрата.
- 1)), либо с косой новгородской Кн(Ст:Кн = 1:√2). Если же на новгородской трости брались мерные полусажени в паре с малой саженью, то эта пара давала золотое сечение (См/2:Ст=φ). Итак, красота пропорций древнерусской архитектуры заложена в самой системе древнерусских мер, дающей такие важнейшие пропорции, как золотое сечение, функция золотого сечения, отношение двойного квадрата.
Но помимо всех этих пропорций, которые от самой природы перешли в систему мер, а затем и в архитектурные памятники, был у древнерусских мастеров и еще один секрет. Именно этот секрет позволял придавать каждому древнему сооружению неповторимую прелесть, "нюанс", как говорят архитекторы. Секрет этот раскрыт в рядной записи плотника Федора на постройку деревянной церкви Усть-Кулуйского погоста (кон. XVII в.), где сказано: "А рубить мне, Федору, в высоту до порога 9 рядов, а от полу до поволоки - как мера и красота скажет..."
"Как мера и красота скажет..." Эта замечательная формула безвестного русского плотника выражает суть диалектики взаимодействия рационального (мера) и чувственного (красота) начал в достижении прекрасного, союз математики (мера) и искусства (красота) в создании архитектурных памятников.
Перейдем, наконец, к анализу пропорций церкви Покрова на Нерли. Этот архитектурный шедевр для русского человека значит столько же, сколько Парфенон для грека. Поэтому неудивительно, что пропорциональный строй небольшой церкви анализировался многими исследователями и каждый из них старался дать свою "окончательную" разгадку тайны ее очарования. Рассмотрим кратко и мы пропорции церкви Покрова на Нерли с двух точек зрения.
Согласно архитектору Шевелеву, в основе пропорционального строения церкви Покрова лежит отношение сажени без чети к мерной сажени, которое является функцией золотого сечения (Сч:См = √5:2), а сам план церкви был построен следующим образом. Вначале размечался прямоугольник длиной 3 сажени без чети и шириной 3 мерные сажени, который очерчивал столбы, несущие барабан и своды. Поскольку 3Сч: 3См = √5:2 = 1,118, то стороны этого прямоугольника относятся к функции золотого сечения, а сам прямоугольник является почти квадратом, или, в терминологии Жолтовского, "живым квадратом". Проведя в исходном прямоугольнике диагонали, зодчий получал центр храма, а отложив на диагоналях от вершин к центру по 1 мерной сажени,- подкупольный прямоугольник и размеры несущих столбов. Так было построено ядро плана, определявшее все дальнейшие горизонтальные и вертикальные размеры сооружения. Мерная сажень строителей церкви Покрова равнялась См = 1,79 м.
Отмерив от Центра храма на восток 3См и на запад 3Сч, мастер получал длину внешнего прямоугольника, равную 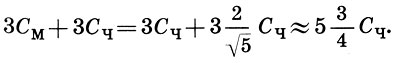 . А отложив этот размер в мерных саженях,- его ширину 53/4См. Таким образом, внешний прямоугольник плана церкви подобен ядру плана и также является "живым квадратом". Диагональ подкупольного прямоугольника определила диаметр центральной абсиды (подкупольного алтарного выступа) и диаметр барабана храма. Короткая сторона подкупольного прямоугольника задавала диаметры боковых абсид.
. А отложив этот размер в мерных саженях,- его ширину 53/4См. Таким образом, внешний прямоугольник плана церкви подобен ядру плана и также является "живым квадратом". Диагональ подкупольного прямоугольника определила диаметр центральной абсиды (подкупольного алтарного выступа) и диаметр барабана храма. Короткая сторона подкупольного прямоугольника задавала диаметры боковых абсид.
Наконец, высота основания храма - четверика, читаемая по высоте тонких колонок,- равна удвоенной длине ядра плана, т. е. 2*3Сч = 6Сч, а высота барабана с шлемовидной главой* - удвоенной ширине ядра, т. е. 2*3См = 6См. Таким образом, главные вертикальные размеры храма - высота основания и высота завершения - также относятся в функции золотого сечения. Сам же четверик представляет собой "почти куб", основанием которого является "почти квадрат", а высота почти равна сторонам основания. Итак, в построении четверика храма явно виден принцип приблизительной симметрии, который так часто встречается в природе и искусстве (см. гл. 4). Можно указать и на более мелкие членения храма, относящиеся в функции золотого сечения, т. е. в отношении сажени без чети к мерной сажени. Например, каменный поясок, венчающий колончатый фриз, который охватывает всю церковь и является ее важной архитектурной деталью, делит высоту четверика в функции золотого сечения.
* (Первоначально церковь Покрова имела характерный для древнерусских храмов шлемовидный купол, напоминавший шлем воина. В XVII веке шлемовидный купол был переделан на луковичный, который мы и видим сегодня.)
Рассмотрим теперь ихнографию храма Покрова на Нерли, какой ее видит знаток древнерусской архитектуры К. Н. Афанасьев. Согласно Витрувию, "ихнография есть надлежащее и последовательное применение циркуля и линейки для получения очертаний плана". Как считает Афанасьев, исходным размером церкви Покрова является меньшая сторона подкупольного прямоугольника, равная 10 греческим футам: а = 10 греч. фут. = 308,7 см. Тогда большая сторона подкупольного прямоугольника получается как диагональ двойного квадрата со стороной а/2. Таким образом, подкупольный прямоугольник является "живым квадратом", стороны которого соотносятся в функции золотого сечения. Толщина столбов определяется отношением золотого сечения к модулю а/2. Дальнейшие построения ясны из рисунка. Так строится ядро плана. Остальные размеры плана получаются аналогичными построениями, опираясь в основном на модуль а/2.
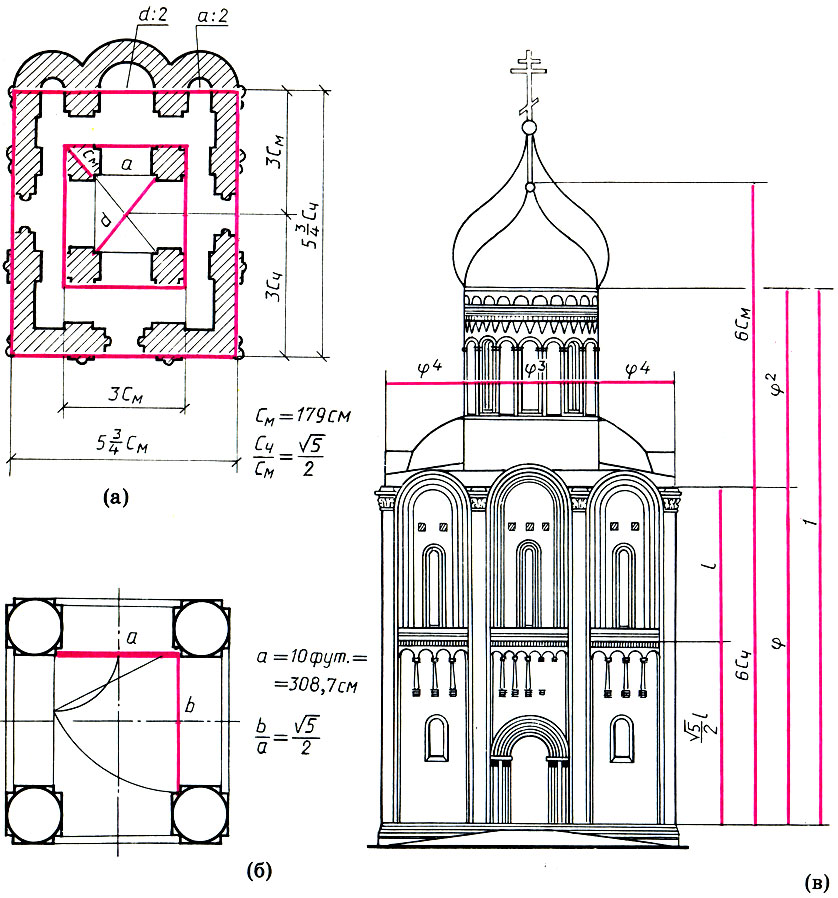
Пропорции церкви Покрова Богородицы на Hepли. Построение плана с помощью парных мер по Шевелеву (а). Геометрическое построение ядра плана по Афанасьеву (б). Некоторые пропорциональные членения западного фасада (в)
Заметим, что вместе с функцией золотого сечения закон золотого сечения также определяет пропорциональный строй церкви Покрова. Это неудивительно, ибо данные отношения связаны геометрией двойного квадрата. Как установил Афанасьев, закону золотого сечения подчинены прежде всего главные вертикали храма, определяющие его силуэт: высота основания, равная высоте тонких колонок четверика, и высота барабана. Диаметр барабана относится к его высоте также в золотой пропорции. Эти пропорции видны с любых точек зрения. Переходя к западному фасаду, ряд золотого сечения можно продолжить: плечи храма относятся к диаметру барабана в золотой пропорции. Итак, принимая высоту белокаменной части церкви (от цоколя до купола) за единицу, мы получаем ряд золотого сечения: 1, φ, φ2, φ3, φ4, который определяет силуэт архитектурного сооружения. Этот ряд можно продолжить и в более мелких деталях. (Разумеется, западный фасад с точки зрения золотой пропорции не составляет исключения и взят нами лишь в качестве примера.)
Подведем некоторые итоги. Мы видим, что непостижимая, казалось бы, гармония храма Покрова подчинена математически строгим законам пропорциональности. План церкви построен на пропорциях функции золотого сечения - "живых квадратах", а ее силуэт определяется рядом золотого сечения. Эта цепь математических закономерностей и становится волшебной мелодией взаимосвязанных архитектурных форм. Конечно, законы пропорциональности определяют только "скелет" сооружения, который должен быть правильным и соразмерным, как скелет здорового человека. Но помимо математических законов меры в недрах архитектурного шедевра непременно заложены и непознанные законы красоты: "как мера и красота скажет..."! Именно диалектика взаимодействия законов меры и законов красоты, которые часто проявляются в отклонениях от законов меры, и создает неповторимый образ архитектурного шедевра.
Заметим, что с точки зрения геометрии рассмотренные нами реконструкции пропорционального строения церкви Покрова аналогичны. Они согласуются между собой и дают в плане три вписанных друг в друга "живых квадрата", отношение сторон которых √5:2 определяет весь пропорциональный строй храма. Однако с точки зрения истории архитектуры эти реконструкции отличаются принципиально. Первая из них основана на древнерусской системе мер и, следовательно, предполагает, что церковь Покрова была построена русскими зодчими. Вторая же в качестве основного размера имеет греческую меру и потому дает основание считать, что церковь строилась приглашенными из Византии мастерами... Кто и как создал жемчужину русской архитектуры? Возможно, мы еще узнаем ответ и на этот вопрос...
Церковь Покрова была построена в 1165 г. А через 73 года она стала свидетельницей небывалой в истории России беды: полчища Батыя, превратив в пепелище Рязань, Коломну и Москву, осадили Владимир. Русскому государству, истерзанному княжескими раздорами, был нанесен смертельный удар, оправиться от которого в полной мере Россия смогла только через 200 лет, к концу XV века.

Церковь Вознесения в селе Коломенском (ныне Москва). 1532. Шедевр древнерусского зодчества, один из первых каменных шатровых храмов на Руси
В 1530 г. в царской усадьбе - селе Коломенском под Москвой - родился будущий царь пробуждающейся России Иван Грозный. А через два года здесь же, в Коломенском, на крутом берегу Москвы-реки, было завершено строительство церкви, поставленной в память об этом событии. Зодчие будто предвидели рождение небывало грозного царя: церковь тоже была небывалой. В ней все", и высота (почти 62 м), и каменный шатер, и устремленная ввысь форма - было невиданным. Новый храм словно символизировал прорыв России в свободное от татарского ига будущее. "...Бе же церковь та велми чюдна высотою и красотою и светлостию, такова не бывала прежде на Руси",- писал о ней летописец. Весь пропорциональный строй церкви, все ее безудержное стремление ввысь как нельзя более соответствовали названию - храм Вознесения.
Но для нас храм Вознесения интересен еще и тем, что он является не только гимном расправляющей крылья России, но и архитектурным гимном геометрии.
Ни один из рассмотренных архитектурных шедевров, в том числе и Парфенон, не настолько пронизан геометрией, не настолько прост и лаконичен в своей размерной структуре, как храм Вознесения в Коломенском. Соразмерности храма с предельной ясностью определены двумя парными мерами: горизонтальные - малой (тмутараканской) саженью Ст и косой новгородской саженью Кн (Ст:Кн = 1:√2), вертикальные - малой саженью Ст и мерной саженью См (Ст:См = 1:(√5 - 1)) и их комбинацией См:2Ст= (√5 - 1):2 = φ, дающей золотое сечение. Таким образом, храм Вознесения является также прекрасным примером применения московскими мастерами измерительного инструмента типа новгородской мерной трости, созданной, как мы помним, для работы именно этими двумя парами мер (см. с. 220). Рассмотрим пропорциональ-ный анализ храма, сделанный архитектором Шевелевым.
В основу плана церкви Вознесения положен квадрат ABCD со стороной в 10 малых сажень: а = АВ = 10Ст. Ясно, что диагонали квадрата равны 10 косым новгородским саженям: AC = BD = 10√2СТ = 10Кн. Так с помощью парных мер Ст и Кн осуществлялся контроль правильности построения исходного квадрата. Окружность радиуса R = 5Kн, описывающая квадрат, определяет положение всех 12 наружных углов плана храма. Вписав через середины сторон в квадрат ABCD новый квадрат и сделав построения, мы получим внешний контур плана - 20-уголъник. Выступающие над исходным квадратом части называются притворами, их ширина равна а/2 = 5Ст. Выразив радиус описанной окружности R в мерных саженях и отложив эту величину в малых саженях, строители получали сторону квадрата b, определяющего внутреннее пространство храма:
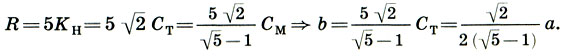
Разумеется, коломенские мастера не вычисляли никаких радикалов! Они просто прикладывали мерную трость разными сторонами и автоматически переходили из одной меры в другую. План церкви построен. А мы выразим еще сторону квадрата с, охватывающего притворы: с = √7/2а (треугольник, из которого находится с/2, на чертеже не показан, чтобы не портить красоту центральной симметрии плана; найдите его). Зная а, b, с, легко выразить все остальные размеры плана и соотношения между ними.
Перейдем к объемам и вертикальным членениям храма. Церковь Вознесения со всех сторон окружена крытой галереей, поднятой над уровнем земли и называемой гульбищем. Гульбище делалось на уровне перекрытия подклета - полуподвального помещения, используемого в хозяйственных целях. Вход в церковь устраивался с гульбища, на которое в храме Вознесения ведут три крыльца, и, таким образом, вертикальные размеры церкви с гульбищем воспринимаются от уровня последнего.
Основной объем храма составляет 20-гранная призма, поставленная на подклет. Ее высота равна стороне исходного квадрата а. Таким образом, ядром основного объема является куб - четверик а×а×а (а=10Ст), украшенный гранями притворов. Вместе с подклетом высота 20-гранной призмы равна диагонали исходного квадрата а√2 = 10√2Ст = 10Кн. Итак, сторона и диагональ исходного квадрата (ядра плана) полностью определяют вертикальные размеры основного объема (ядра основания).
Двадцатигранная призма основного объема через затейливый пояс кокошников переходит в восьмигранную призму - восьмерик. Восьмерик также вписан к куб d×d×d(d = 9Cт). Затем восьмерик переходит в восьмигранный шатер, высота которого h = d√2 = 9√2Ст = 9Кн, т. е. шатер вписан в прямоугольный параллелепипед 9Ст×9Ст×9Кн. Площадь верхнего сечения шатра уменьшена в 16 раз, а его линейные размеры - в 4 раза. Поскольку 1/4 сажени равна локтю, то, следовательно, верхнее сечение вписано в квадрат где Лт - малый (тмутараканский) локоть (4Лт = Ст). Наконец, через венчающий карниз шатер завершается восьмигранным барабаном, сечение которого на малый полулокоть превышает верхнее сечение шатра. Барабан чуть нависает над шатром и вписан в куб f×f×f (f = 9,5Лт), а вместе с главкой, взятой без яблока (см. рис. на с. 242), барабан вписан в прямоугольный параллелепипед f×f×√2f.
Итак, мы видим как сторона ядра плана а, измеренная то малой саженью, то косой новгородской, рождает все главные вертикали храма. Заметим, что общая высота церкви от верха цоколя до яблока, на котором стоит крест, равна 4а = 40Ст, т. е. также простейшим образом выражается через исходный размер а. И еще одно важное отношение. Пояс кокошников, через который четверик основания переходит восьмерик шатра, делит храм на две части - основание и завершение. Высота основания h1≈14Cт, а высота завершения h2≈14Kн, откуда h1:h2 = Cт:Kн = 1:√2, т. е. главные вертикальные членения храма также относятся как малая и косая новгородская сажени.
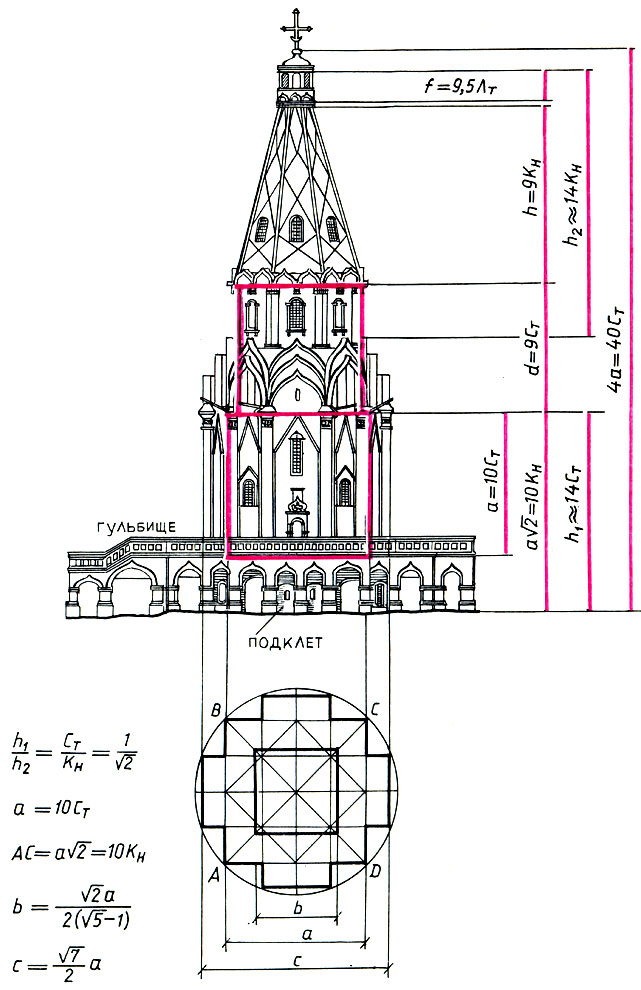
Пропорциональный строй церкви Вознесения в Коломенском (по Шевелеву)
Но пропорции храма Вознесения определены не одной, а двумя математическими закономерностями. Помимо пропорции Ст:Кн= 1:√2, определяющей основание, статическое начало храма, есть в нем и другая тема - тема развития вверх, вознесения, которая определена пропорциональной цепью: Ст:См = 1:(√5 - 1), а также пропорцией золотого сечения: См:2Ст=φ. В проведении этой темы соблюден знакомый нам по Парфенону принцип встречного движения пропорций. Две разные пропорциональные цепи накладываются друг на друга, сталкиваются и противоборствуют. В этом столкновении двух противоборствующих начал - горизонтального и вертикального - и заключается архитектурный образ церкви Вознесения. Не останавливаясь на математическом анализе этих двух систем, предоставим слово автору прекрасного эстетического анализа церкви Вознесения, искусствоведу А. Циресу. "В образе этой церкви,- пишет Цирес,- сплетаются два основных лейтмотива: мотив острого, полного столкновений и диссонансов динамизма и мотив гармонически спокойной красоты... Сложный ритм арок нижних галерей... идет, учащаясь от краев к центру,... теснит арки от краев к углам основного массива церкви и к ее середине,... подсказывает смену горизонтального движения движением, направленным ввысь... Так снизу вверх идет последовательное смягчение кристаллизма и нарастание компактности объема, вплоть до его стянутости в крепкий узел, венчающий всю объемную композицию главкой".
Но закончить разговор о пропорциях церкви Вознесения в Коломенском нам хочется словами автора математического анализа ее пропорций, Шевелева. "Подчеркнем выразительнейшую деталь размерной структуры, наиболее ярко показывающую особенность логики древнего мастера, стремящегося особенно точно выразить в метрологии главное. Так же как 10 саженей определили, по существу, весь храм, его ядро, так же и 10 локтей определили символ и венчание церкви - крест (10СтХ10СтХ10Ст - четверик; 10СтХ10СтХ10Кн - призма четверика; 10ЛтХ10Лт - соразмерность креста, ибо в нем заключен для зодчего и смысловой символ соединения, и символ торжества вертикали, и символ храма, и символ пропорции, построившей этот образ)".
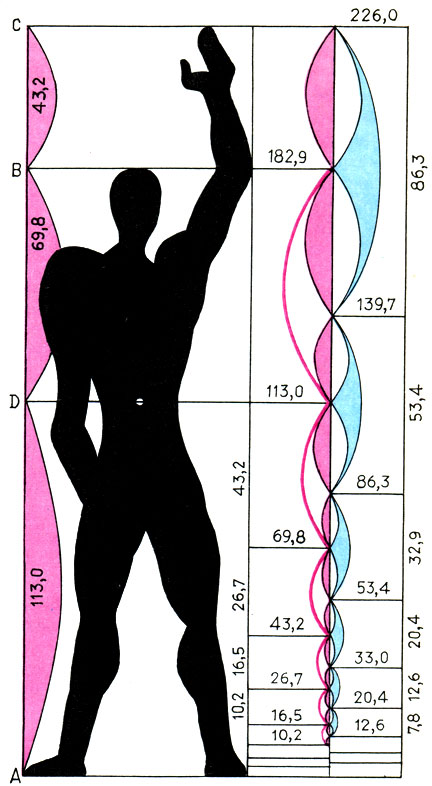
Модулор Ле Корбюзье. Рисунок Ле Корбюзье. 'Модулор - это измерительный прибор, в основе которого лежат человеческий рост и математика' (Ле Корбюзье)
Нам остается только добавить, что село Коломенское давно уже стало частью современной Москвы и тем, кто не знает этого, мы рекомендуем сойти на одноименной станции метро и воочию убедиться в гениальности безвестных русских мастеров. Ну а те, кто знаком с храмом Вознесения, быть может, захотят теперь взглянуть на него другими глазами, увидеть в нем не только причудливую игру воображения художника, но и мудрый расчет изощренного ума мастера.
Коль скоро речь у нас зашла о метро, то перенесемся, наконец, в современный XX век. Время поисков пропорций и сегодня не кануло в Лету, напротив, по мнению Ле Корбюзье, оно только настало.
Мы уже отмечали (с. 220), что антропометрические меры благодаря своему происхождению оказались как нельзя лучше приспособлены для конструирования архитектурной среды. Мы только что убедились в том, что антропометрические меры содержали в себе замечательные пропорции, позволявшие древним мастерам создавать прекрасные памятники архитектуры.
7 апреля 1795 г. во Франции была введена метрическая система мер, в разработке которой участвовали такие крупнейшие ученые, как Лаплас, Монж, Кондорсе. За единицу длины - метр - была принята 1/10 000 000 часть 1/4 длины парижского географического меридиана. Метрическая система обладала бесспорными преимуществами и все шире раздвигала границы своего существования. Однако метр никоим образом не был связан с человеком, и, по мнению Ле Корбюзье, для архитектуре это имело самые серьезные последствия^ "Принимая участие в постройке хижин, жилых домов, храмов, предназначенных для потребностей человека, метр, по-видимому, ввел в них чужие и чуждые единицы измерения и, если мы присмотримся к нему ближе, может быть обвинен в дезориентации современной архитектуры и ее искажении... Архитектура, построенная на метрических измерениях, сбилась с правильного пути".
Но главная причина, толкавшая зодчих XX века на поиски новых систем измерений в архитектуре, была все-таки не в недостатках метрической системы мер. Английская архитектура с постоянством продолжала пользоваться футами и дюймами, но и у нее возникли те же проблемы. Дело было в том, что вместе с XX веком в архитектуру пришли невиданные объемы и темпы строительства. Проектирование архитектурной среды стало преимущественно типовым, а сама архитектура - индустриальной. В этих условиях строительные элементы необходимо было стандартизировать и унифицировать. Кроме того, архитекторам хотелось бы примирить непримиримое: красоту и стандарт. Требовалось найти такие методы пропорционирования, которые обладали бы максимальной гибкостью, простотой и универсальностью. "Если бы появился какой-нибудь линейный измеритель, подобный системам музыкальной записи, не облегчился бы ряд проблем, связанных со строительством?" - спрашивал Ле Корбюзье. И в 1949 г. он сам отвечает на этот вопрос, предложив в качестве такого измерителя систему модульной унификации - модулор.
Идея построения модулора гениально проста. Модулор - это ряд золотого сечения (15.2):
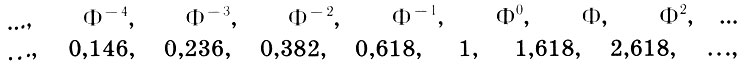 (17.1)
(17.1)умноженный на два коэффициента. Первый коэффициент k1 равен росту человека; умножая (17.1) на k1, Корбюзье получает так называемый красный ряд. Второй коэффициент k2 равен расстоянию от земли до конца поднятой руки человека (это большая сажень в древнерусской системе мер)- При умножении (17.1) на k2 получается синий ряд. Осталось только выбрать числовые значения коэффициентов. Желая примирить в моду лоре английскую и французскую системы мер, а также следуя античной традиции, согласно которой рост человека равен 6 футам, Корбюзье взял в качестве k1 6 английских футов, т. е. k1 = 6*30,48 = 182,88 см. Значение k2 принято равным 226,0 см. Так были получены красный ряд:
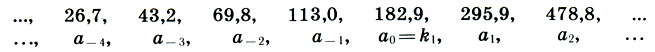 (17.2)
(17.2)и синий ряд:
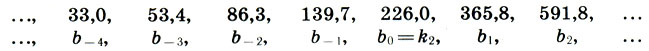 (17.3)
(17.3)Значение k2 было выбрано еще и так, чтобы между красным и синим рядами существовала простая связь:
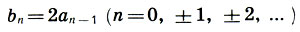 (17.4)
(17.4)Следовательно, синий ряд фактически есть удвоение красного ряда.
Будучи геометрическими прогрессиями, члены обоих рядов модулора образуют цепь равных отношений: an+1:an = bn+1:bn = Φ, т. е. в моду лоре воплощается принцип гармонии: "из всего - единое, из единого - все". Благодаря аддитивному свойству золотого сечения "части" модулора сходятся в "целое". Наконец, абсолютные значения шкал модулора происходят от человека и потому хорошо приспособлены для проектирования архитектурной среды. Так, по мнению автора, модулор вносит порядок, стандарт в производство и в то же время связывает все его элементы законами гармонии.
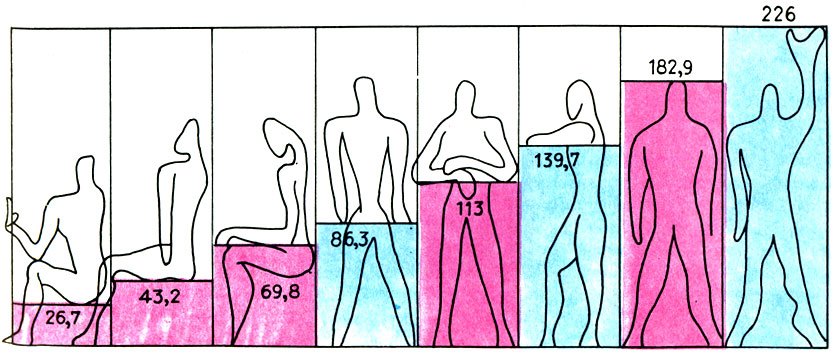
Числа красной и синей шкал модулора - действительные размеры, соответствующие определенным положениям тела человека. Рисунок Ле Корбюзье

Капелла в Роншане. 1958 (б). Эти два антипода в творчестве великого зодчего, две различные философии в архитектуре связаны воедино гаммой архитектурных пропорций - модулором

Ле Корбюзье. 'Лучезарный дом' в Марселе. 1947-1952 (а). Эти два антипода в творчестве великого зодчего, две различные философии в архитектуре связаны воедино гаммой архитектурных пропорций - модулором
Однако "погоня за двумя зайцами" (желание иметь хорошие числа и в метрах, и в футах) вылилась в серьезный недостаток: размеры модулора оказались несоразмерными со средним ростом человека. Широкого распространения модулор не получил. Но идеи стандарта и гармонии, заложенные в модулоре, не перестают волновать архитекторов. Вечный поиск совершенной гармонии продолжается. Недавно советским, архитектором Я. Д. Гликиным разработана универсальная система пропорциональности, которая, как показывает автор, вбирает в себя все известные до сего времени системы пропорционирования: системы триангулирования на египетском и на равностороннем треугольнике; системы Вйтрувия, Альберти, Хэмбриджа, Месселя, Шевелева; систему древнерусских мер и модулор Ле Корбюзье.
Что же объединяет все системы пропорциональности? Дело в том, что любая пропорциональная система - это основа, скелет архитектурного сооружения, это та гамма, а точнее, тот лад, в котором будет звучать архитектурная музыка. Именно это свойство модулора Ле Корбюзье имел в виду Альберт Эйнштейн, давая ему восторженную оценку: "Модулор - это гамма пропорций, которая делает плохое трудным, а хорошее - легким". Но гамма - это еще не мелодия, не музыка. Это хорошо осознавал и сам Корбюзье: "Модулор - это гамма. Музыкант располагает гаммой и создает музыку по своим способностям - банальную или прекрасную". В самом деле, как гамма уже третье тысячелетие дает возможность композитору создавать бесконечное разнообразие мелодий, так и система пропорционирования - модулор - нисколько не стесняет в творчестве архитектора. Сам
Корбюзье блестяще доказал это, построив с помощью своего модулора и знаменитый "Лучезарный дом" в Марселе, и не менее знаменитую капеллу в Роншане. Эти два произведения великого зодчего - два антипода, две разные философии в архитектуре. С одной стороны, воплощение здравого смысла, ясного, прямолинейного и рационального. С другой - нечто иррациональное, пластическое, скульптурное, сказочное. Единственное, что объединяет эти два выдающихся памятника зодчества - это модулор, архитектурная гамма пропорций, общая для обоих произведений Ле Корбюзье.
Но почему великий Эйнштейн систему пропорционирования в архитектуре - модулор - сравнивает с музыкальной гаммой? Почему его великий соотечественник Гёте называет архитектуру отзвучавшей музыкой? Что общего между архитектурой и музыкой? Это и будет последний вопрос, на который мы попытаемся ответить в этой части книги.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'