16. Пропорции: от Парфенона до Нотр-Дама

...Вся наша Франция заключена в наших соборах, как и вся Греция сжата в одном Парфеноне.

О. Роден

"Человек - мера всех вещей..." Этот знаменитый афоризм древнегреческого философа-софиста Протагора (ок. 490 - ок. 420 до н. э.) является ключом к разгадке тайны пропорций Парфенона, его поразительной гармонии и спокойствия. Как это ни парадоксально, но между живыми линиями человеческого тела и застывшими на тысячелетия каменными очертаниями древнего сооружения существует глубокая связь, выраженная в математических законах пропорциональности. Но по порядку...

Мы уже знаем о многих теориях античных пропорций, пытавшихся объяснить гармонию Парфенона на основе золотого сечения (см. гл. 14). Такой подход понятен ввиду особой роли золотого сечения как в природе, так и в искусстве, роли, которая во многом еще остается загадочной. Кроме того, апологеты золотого сечения ссылались на некоторые высказывания Платона о пропорциях. Однако эти высказывания великого философа, видимо, понимались слишком узко (см. с. 195). В главе 14 мы показали, что многие внешне различные теории пропорций Парфенона математически приводят к золотому сечению в отдельных элементах этого архитектурного шедевра. Но целостной теории на базе золотого сечения все-таки не получалось.

Некоторых исследователей отсутствие единой теории античных пропорций вообще разуверило в принципе пропорциональности. Пессимисты подняли на щит высказывание великого теоретика пропорций XX века Ле Корбюзье о том, что "Парфенон - это более, чем архитектура, это - скульптура". Они объявили математическое исследование пропорций Парфенона кощунством. Действительно, тщательное изучение показало, что в Парфеноне, как и в человеческом теле, нет прямых линий. Линии Парфенона наполнены жизнью и пластикой. Однако это отнюдь не означает, что в них нет пропорциональной зависимости, той самой, которую так одержимо искали и находили в теле человека Поликлет, Леонардо да Винчи, Дюрер и др.

А оптимисты продолжают поиск законов строения архитектурных шедевров, поиск тех вечных истин, которые, возможно, являются общими законами формообразования и в природе, и в искусстве. Оригинальную теорию разрабатывает в течение последних двадцати лет архитектор И. Ш. Шевелев. Это теория парных мер, которая настолько естественна, что просто удивительно, почему она до середины XX века никому не пришла в голову. Парные меры - это два эталона длины а и Ь, которые позволяли устанавливать одинаковые отношения между отдельными парами архитектурного сооружения a:b = na:nb (n = 1, 2, 3, ...). Какие же величины выступали в качестве парных мер? Сама история развития математики указывает на то, что это были геометрические объекты: сторона и диагональ прямоугольника. В самом деле, математика начиналась с геометрии, а слово "геометрия" означает землемерие. Основной задачей последнего было измерение площадей земельных участков. Древнейшим методом измерения площадей был метод приложения, суть которого состояла в следующем. К измеряемому прямоугольнику прикладывается эталон площади (как правило, квадрат). В прямоугольнике, образованном стороной эталона и стороной измеряемого участка, проводилась диагональ до пересечения с продолжением второй стороны эталона.

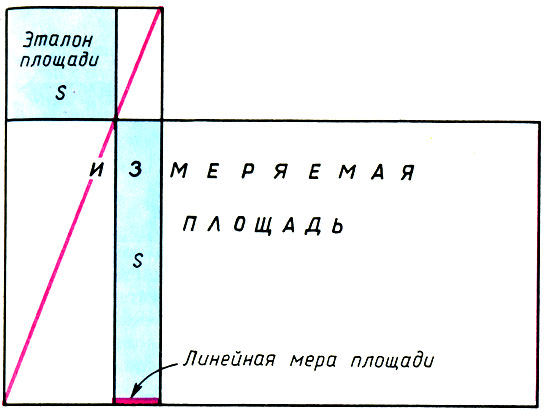
Измерение площади прямоугольного участка 'методом приложения'

Получалось три прямоугольника. Два из них, через которые прошла диагональ, подобны, а третий равновелик эталону (докажите это). Сторона равновеликого прямоугольника и служила линейной мерой для определения площади. Так измерение площади сводилось к простому подсчету числа линейных мер в стороне измеряемого прямоугольника. Так сторона и диагональ прямоугольника становились основными инструментами древних землемеров-математиков.

Из всего множества прямоугольников квадрат и двойной квадрат обладают тем практическим преимуществом, что требует для построения прямого угла не три, а две меры (в двойном квадрате большая сторона получается двукратным отложением малой). Так появились парные меры 1:√2 и 1:√5 (см. с. 199).

Знания, накопленные в геометрии, использовались и в архитектуре. Древние зодчие были прекрасными математиками. Но в отличие от землемерия архитектура обладает третьим измерением - высотой. Поэтому стороны и диагональ прямоугольника, проведенные на земле, пришлось заменить мерными палками, которыми можно было оперировать и в третьем измерении. Парную меру двойного квадрата 1:√5 мы и видим в руках древнеегипетского зодчего Хесиры (см. с. 200).

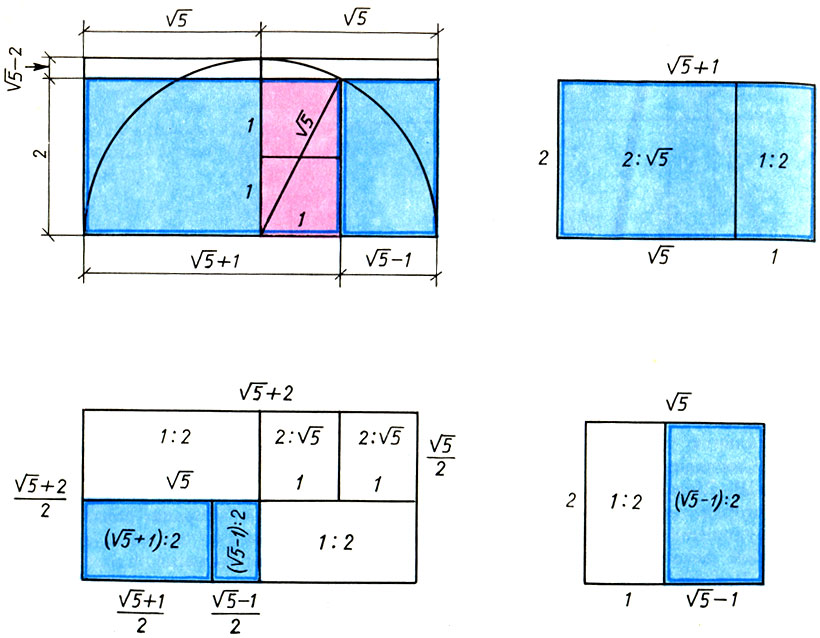
Геометрические свойства системы двух квадратов. Исходный двойной квадрат показан красным, прямоугольники золотого сечения - синим. Рисунок демонстрирует также аддитивное свойство прямоугольников системы двойного квадрата

Парная мера 1:√5 встречается во множестве древних сооружений, разделенных между собой веками и тысячами километров: пирамиды Джосера, Хеопса, Хефрена и Миккерина, пропорции Парфенона и Эрехтейона, церковь Покрова на Нерли и храм Вознесения в Коломенском, древние храмы Киева и Новгорода...

Разумеется, причина популярности этой парной меры не только в том, что для построения прямого угла с ее помощью требуются именно две, а не три меры. Истинная причина заключена в разнообразии математических свойств двойного квадрата.

В самом деле, возьмем квадрат со стороной 1, построим двойной квадрат (т. е. прямоугольник со сторонами 1 и 2), проведем в нем диагональ и опишем ею полуокружность (см. рис. ). Так мы построим новый двойной квадрат с малой стороной √5. Продлив стороны исходного двойного квадрата до пересечения со сторонами нового, мы получим целую гамму пропорций, содержащую практически все коэффициенты пропорциональности от 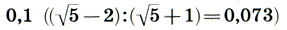до 1 с шагом 0,1:

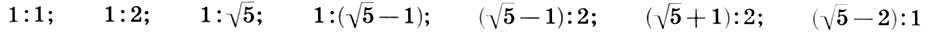
и т. д. Заметим: двойной квадрат тесно связан с золотым сечением. Так, в результате наших построений мы получили два прямоугольника золотого сечения, выделенные синим цветом: 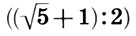и .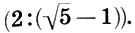

Ну а какое отношение математика двойного квадрата имеет к архитектуре? Широкое распространение в архитектуре пропорции двойного квадрата, как и пропорции золотого сечения, получили благодаря свойству, которое по аналогии с золотым сечением можно назвать аддитивным свойством площадей. Дело в том, что каждое архитектурное произведение или его часть можно вписать в прямоугольник. Так вот, прямоугольники системы двойного квадрата могут без остатка разлагаться на другие прямоугольники этой же системы. Это и есть аддитивное свойство площадей системы двух квадратов, аналогичное линейному аддитивному свойству золотого сечения. Например, прямоугольник золотого сечения (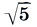+1) одной линией можно разделить на два прямоугольника, стороны которых будут относиться как 1:2 и 2: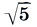, а прямоугольник со сторонами 2 и 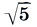легко разложить на "золотой" прямоугольник (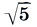-1):2 и двойной квадрат 1:2. Прямоугольник 1:2 четырьмя линиями разбивается на шесть прямоугольников: два неравных прямоугольника 1:2, два равных прямоугольника 2: √5 и два неравных "золотых" прямоугольника (√5 - 1): 2. И т. д. Таким образом, система двух квадратов дает поразительное разнообразие разбиений целого на части, находящиеся в тех же пропорциональных отношениях. Так, благодаря аддитивному свойству площадей системы двух квадратов достигается взаимосвязь целого и его частей, осуществляется основной принцип гармонии: "из всего - единое, из единого - все".

Заметим, что получаемые в системе Двух квадратов прямоугольники с отношением сторон 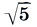:2≈1,118 близки к квадратам, а само отношение √5:2 представляет так называемую функцию золотого сечения, введенную архитектором Жолтовским. В терминах ряда золотого сечения (15.5) функция золотого сечения определяется как отношение

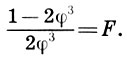
Поскольку 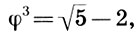, то мы легко получаем

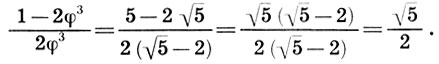
Прямоугольник с отношением сторон 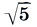:2 Жолтовский называл "живым квадратом", считая, что он должен заменить в архитектуре математический квадрат, который не встречается в природе и не радует глаз своей пропорцией (1:1). Будучи большим энтузиастом золотого сечения и его функции, Жолтовский нашел многочисленные примеры этих пропорций в архитектурных шедеврах, в том числе и в Парфеноне (см. с. 202). Итак, среди многих пропорций, обладающих аддитивным свойством площадей, двойной квадрат содержит и такие "выдающиеся" пропорции, как золотое сечение и функцию золотого сечения.

Теория парных мер родилась в 60-е годы. Однако, кроме мерных палок Хесиры, эта теория реальных подтверждений не имела и, по существу, оставалась гипотезой, построенной на математических рассуждениях. Правда, пропорциональные циркули (см. с. 199) также представляют собой парные меры. Но это меры, с помощью которых строился чертеж архитектурного сооружения, а не само сооружение. И вот в 1970 г. теория парных мер получила еще одно блестящее доказательство. При археологических раскопках в Новгороде экспедицией члена-корреспондента АН СССР А. В. Арциховского был найден обломок мерной трости конца XII века. Мерная трость представляет собой брусок прямоугольного сечения, на трех гранях которого нанесены три различные шкалы. 24 деления каждой из шкал дают разные сажени: тмутараканскую (С_т= 142,1 см), мерную (С_м = 175,6 см) и косую новгородскую (К_н = 200,9 см). Но ведь это не что иное, как парные меры системы двух квадратов! В самом деле, С_т : С_м = 1:(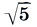 - 1) = 0,809, С_т:К_н = 1:√2 = 0,707. (Подробнее о древнерусских парных мерах и системах пропорционирования мы поговорим в следующей главе.) Так мерная трость^*, а вместе с ней и парные меры из математических абстракций перешли в область реального. Так в нетрадиционной области - теории архитектуры - еще раз проявилось удивительное свойство математики совершать открытия "на кончике пера". Так геометрия двойного квадрата связала воедино мерные палки Хесиры, античные пропорциональные циркули и новгородскую мерную трость.

^* (Первые упоминания о мерной трости имеются в библейских текстах, рассказывающих о строительстве храма царя Соломона и относящихся к X веку до н. э. )

Вернемся, наконец, к теории пропорций Парфенона, к афоризму Протагора: "человек - мера всех вещей". Для древнегреческой философии, искусства и религии всегда было характерно очеловечивание сил природы - антропоморфизм. Даже греческие боги были подвержены человеческим слабостям и страстям. Архитектура в антропоморфизме греков не составляла исключения. Вот что по этому поводу писал тонкий знаток античной архитектуры, профессор Н. И. Врунов: "Ордер классического греческого храма является также главным носителем человеческого начала: он осуществляет на языке архитектуры образ монументализированного человека-героя... Самая форма дорической колонны вызывает ассоциации, связанные с человеческим телом. Прежде всего - вертикализм колонны. Вертикаль - главная ось человеческого тела, основная характерная особенность внешнего облика человека, главное его отличие от облика животного".

Но какой именно математической зависимостью связаны пропорции дорической колонны и человеческого тела? В поисках ответа на этот вопрос роковую роль сыграло следующее высказывание Витрувия: "Желая сделать так, чтобы они (колонны.- А. В.) были пригодны к поддержанию тяжести и обладали правильным и красивым обличьем, они измерили след мужской ступни по отношению к человеческому росту, и, найдя, что ступня составляет шестую его долю, применили это соотношение к колоннаде, и, сообразно с толщиной основания ее ствола, вывели ее высоту в 6 раз больше, включая сюда и капитель. Таким образом, дорийская колонна стала воспроизводить в зданиях пропорции, крепость и красоту мужского тела". Итак, по Витрувию, справедливы отношения: (стопа человека): (высота его тела) = (диаметр колонны): (общая высота колонны) = 1:6. Между тем обмеры дорических колонн упрямо противоречили Витрувию. Неумолимые цифры заставили Брунова отказаться от своих прежних воззрений: "Нельзя утверждать, что дорическая колонна повторяет пропорции тела человека, потому что людей таких пропорций, как колонны Парфенона, не существует". Разгадка была где-то рядом, но ее нашел только в 60-е годы архитектор Шевелев. Вот его решение.

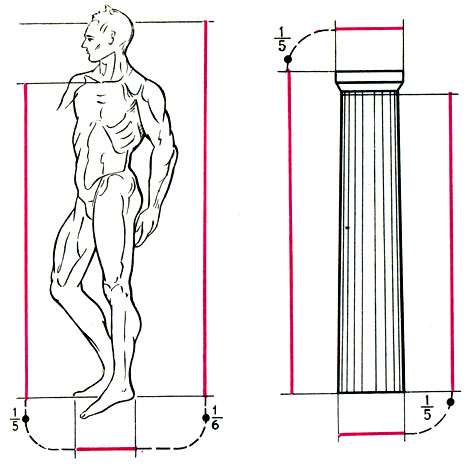
Отношение длины стопы человека к длине его тела от основания шеи до стопы 1:5 - ключ к пропорциональному строю Парфенона (по Шевелеву)

Со времен Поликлета установлено, что если стопу человека принять за единицу измерения - фут (греческий фут = 30,89 см), то рост человека составит 6 футов, а голова вместе с шеей - 1 фут. В этом можно убедиться, глядя на рисунок на следующей странице. Следовательно, на оставшуюся часть тела приходится 5 футов. Именно эта часть и олицетворяет "крепость и красоту мужского тела". В самом деле, в "человеческой колонне" шея - самое слабое место. Груз взваливают на плечи, и даже атланты сгибают шеи и принимают тяжесть на поднятые к голове руки. Эта простая мысль и привела Шевелева к тому, что ствол колонны, несущий тяжесть, должен ассоциироваться не с полным ростом человека, а с его наиболее крепкой частью от стоп до основания шеи. Все сразу стало на свои места. Возникла цепочка пропорций, выполнявшихся с прекрасной точностью:(нижний диаметр колонны):(высота ствола колонны)=(ширина капители по абаке):(высота колонны с капителью) = (стопа человека):(высота человека от стоп до основания шеи)=1:5. Далее, поскольку "подобное в мириады раз прекраснее того, что неподобно" (Витрувий), отношение 1:5 было распространено на всю соразмерность колоннады в целом: (высота колоннады = колонна + антаблемент):(длина храма по стилобату)=1:5.

Мы употребили немало терминов, относящихся к классическому ордеру. Ордер (от лат. ordo - порядок) - это тип архитектурной композиции, названный так Витрувием и основанный на художественной переработке стоечно-балочной конструкции (см. с. 181). Огромную роль в развитии европейской архитектуры сыграли родившиеся в Древней Греции классические ордеры: дорический, ионический и коринфский. Название ордера происходит от названия соответствующей области Древней Греции или Малой Азии. Все последующие архитектурные стили, не говоря уже о зодчестве Возрождения и классицизма, развивались под влиянием классического ордера. Наиболее древний - дорический - ордер (ордер Парфенона) отличается торжественной монументальностью форм, строгостью пропорций и лаконизмом деталей.

Основные элементы дорического ордера, видимые на главном фасаде Парфенона, и их выражение через ширину стилобата: а = 100 фут. = 30,87 м

Итак, в дорической колонне воспроизведены пропорции несущей части мужского тела 1:5. В том же отношении находятся и крайние размеры всего Парфенона - высота колоннады и длина храма. Но вспомним Платона: "невозможно, чтобы две вещи совершенным образом соединились без третьей...", которая является их средним геометрическим (см. с. 195)^*. Следовательно, пропорции Парфенона должны определяться еще одной величиной - средним геометрическим чисел 1 и 5, т. е. 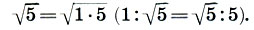Ho ведь √5 есть не что иное, как диагональ двойного квадрата! Таким образом именно парная мера 1:√5 являлся ключом к пропорциональному строению всего Парфенона! Вслед за Шевелевым нам остается только убедиться в справедливости этой гипотезы. В самом деле, между крайними размерами - высотой колоннады и длиной храма - должно лежать и их среднее геометрическое - ширина сооружения. Размеры Парфенона подтверждают это:

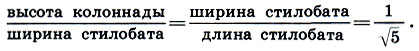(16.1)

^* (Хотя Платон в период строительства Парфенона еще не родился, но сохранившееся в его сочинениях учение о пропорциональности восходит к самому Пифагору и было, безусловно, известно Иктину и Калликрату - зодчим Парфенона.)

Поскольку ширина стилобата точно равна 100 греческим футам, то естественно предположить, что именно этот размер был выбран за исходный размер Парфенона. Итак, если ширина стилобата равна а, то согласно (16.1) его длина b = a√5, a высота колоннады а₁ = а:√5. Так же и шаг колонн связывает всю колоннаду в единое целое и является средним геометрическим диаметра колонны и высоты ее ствола:

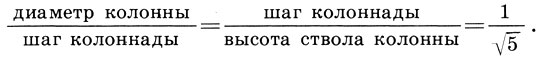(16.2)

Высота колоннады а₁ складывается из высот колонны и антаблемента либо из высот нагрузки а₂ и ствола колонны а₃, т. е. а₁ = а₂ + а₃. Последние две высоты также относятся как 1:√5, откуда легко получить выражение а₃ через а₁.

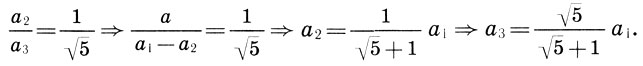
Зная высоту ствола колонны а₃, из (16.2) находим шаг колоннады b = а₃:√5 и диаметр колонны b₂ = b₁:√5.

Далее. В композиции главного фасада Парфенона можно выделить две пары связанных между собой элементов. Первая пара - это два горизонтальных каменных пояса: нагрузка а₂ и стереобат а₄. Эта пара связана числом членений: стереобат и нагрузка содержат по четыре элемента. (Возможно, число элементов в этих парах навеяно учением о четырех стихиях, ибо Парфенон является воплощением в камне всей античной философии.) Вторую пару образуют стволы колонн а₃ и фронтон а₅. Обе пары связаны все тем же законом пропорциональности 1:√5:

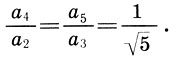(16.4)

Таким образом, "главный фасад оказался зарифмован через строку,- пишет Шевелев.- Причем движение от меньшего к большему (от стереобата к нагрузке), определенное пропорциональной связью первой пары, уравновешено движением от меньшего к большему второй пары (фронтон - ствол колонны), которое противоположно направлено".

Перейдем к оставшимся вертикальным Размерам Парфенона. Высота капители а₇ и диаметр колонны b₂ опять же соотносятся как 1: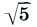, откуда а₇=b₂: 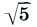= а:5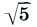( 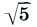+ 1). Зная а₇, легко выразить высоту антаблемента: а₆ = а₂ - а₇ = 4а:5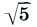( 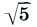+ 1). Наконец, антаблемент а₆ и капитель а₇ разделены одинаково, зеркально-симметрично, в отношении 1:1: 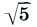на части х, х, х: 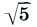и y, y, y: 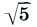соответственно. Тогда из условия x+x+x: 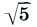= a₆ и у+у+у: 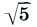= а₇ находим: x = k₂a₆, y = k₂a₇, k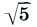₂ = :(2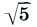 + 1), т. е. находим высоты составляющих антаблемент частей - архитрава а₈ = k₂a₆, фриза а₁₀ = k₂а₆ и карниза a₁₂ = k₂a₆: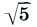, а также высоты элементов капители - абака a₉ = k₂a₇, эхина a₁₁ =k₂a₇ и шейки а₁₃ = k₂а₇:.

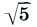Таковы лишь основные идеи пропорционального деления основных элементов Парфенона.

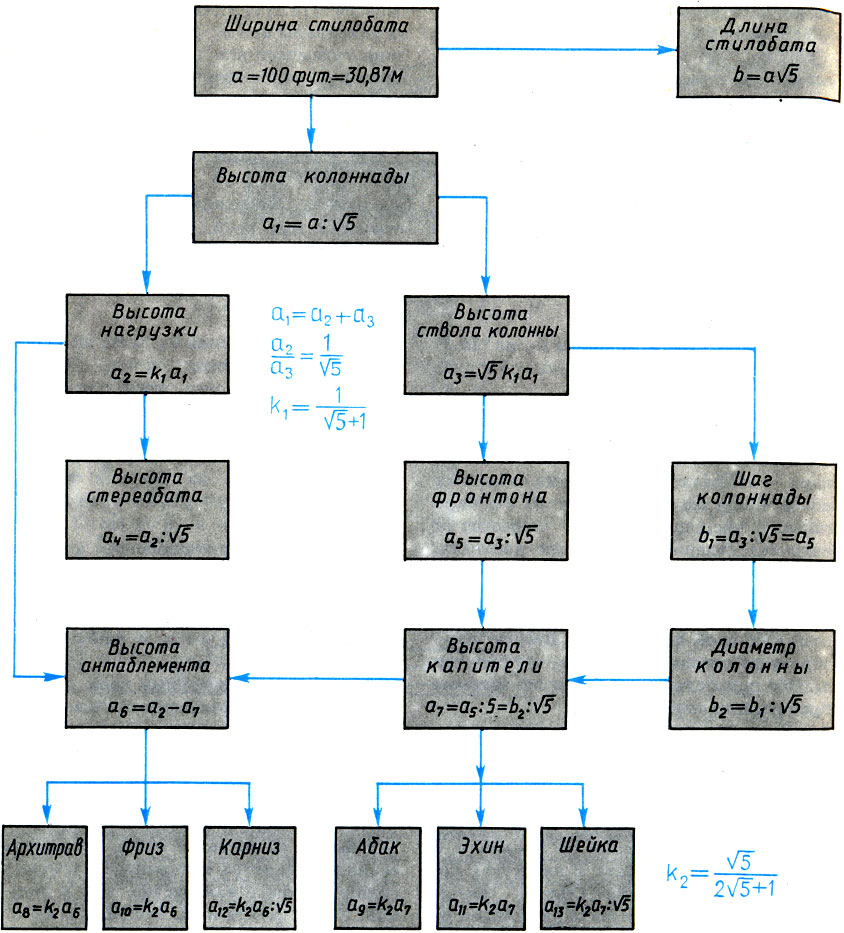
Пропорциональное дерево Парфенона (по Шевелеву). Все размеры храма от длины стилобата b = 69,5 м до высоты шейки а₁₃ = 0,158 м выражаются через ширину стилобата: а = 100 фут. = 30,87 м

А более пытливому исследователю Парфенон открывает и свои более сокровенные тайны. Оказывается, что угловые колонны в Парфеноне толще остальных, рядовых, и сближены с ними. Отношение верхнего диаметра к нижнему в угловых колоннах менее контрастно, чем в рядовых. Такая расстановка колонн логична: ведь и в жизни сильных людей ставят на флангах. Но дело не столько в этом. Дело в том, что угловые колонны смотрятся на фоне яркого неба Эллады. Солнечные лучи дифрагируют, огибают угловые колонны. Поэтому если их сделать одинаковыми с рядовыми колоннами, которые смотрятся на темном фоне целлы - святилища храма, то угловые колонны будут казаться тоньше. Итак, в конструкцию Парфенона введены так называемые оптические поправки.

Древние греки прекрасно знали особенности оптического восприятия человеческого глаза: строго вертикальные и параллельные колонны кажутся распадающимися, а горизонтальная балка - прогнувшейся книзу.

Но даже оптические поправки в Парфеноне подчинены закону 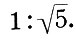Действительно, нижний диаметр угловых колонн больше "теоретического диаметра" b₂ = a:5( 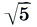+ l) = 190,79 см на 2,96 см, а у рядовых - меньше на 1,32 см. Взяв отношение этих поправок, мы с изумлением обнаруживаем: 1,32:2,96 = 0,446 ≈ 1:( 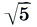= 0,447!

Оптические иллюзии восприятия. Так выглядел бы Парфенон, если бы его линии были строго горизонтальны и вертикальны (а). Таков Парфенон в действительности (б). Парфенон, каким мы его видим благодаря оптическим поправкам (в). Наклоны и искривления прямых сильно преувеличены

Раз уж мы заговорили об отличии "теоретических" размеров Парфенона от истинных, следует расставить все точки над i. Разумеется, совпадение "теоретических" размеров (см. (16.1) - (16.4) и рис. на с. 222) с реальными размерами Парфенона не является абсолютным. Относительные расхождения теории с действительностью колеблются в пределах от 05% до 1,6%. Наибольшее расхождение получается для высоты антаблемента - 3,5%. Это и понятно, ибо высота антаблемента - единственный размер в "пропорциональном дереве Парфенона", полученный не с помощью закона пропорциональности 1:(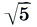, а выражением через другие размеры. Таким образом, антаблемент является наиболее слабым местом в теории Шевелева, и эта слабость теории автоматически проявилась в математической оценке погрешностей. Впрочем, как нам кажется, и такая точность в расстояниях между горизонтальными линиями сооружения (3,5 см на 1 м) является желанным эталоном для некоторых современных строителей.

Заканчивая наш анализ пропорций Парфенона, естественно поставить вопросы: является ли теория Шевелева окончательной теорией Парфенона? Таков ли на самом деле был план построения чертежа Парфенона мудрым Иктином? Ответы на эти вопросы, возможно, даст время. Ибо, как это ни парадоксально, но чем дальше мы уходим от древних, тем лучше мы их узнаем. В этом убеждает нас весь ход развития исторической науки.

И последнее. Внимательный читатель должен задать еще один вопрос: а как теория Шевелева стыкуется с "теориями золотого сечения Парфенона", рассмотренными нами в главе 14? Напомним, что там мы привели к общему знаменателю разнообразные теории пропорций Парфенона, Цейзинга, Жолтовского, Гримма, Хэмбриджа и Месселя и показали, что все они, несмотря на внешнее различие, дают золотое сечение в главных вертикалях Парфенона, т. е. в отношении несущих частей с₁ к несомым с₂ (см. с. 202). А как обстоит дело с этим отношением в теории Шевелева? Из рисунка ясно, что

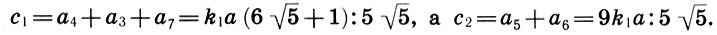
Поэтому

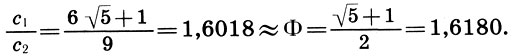(16.5)

Итак, мы выполнили обещание, данное на с. 203, и показали, что и теория Шевелева, столь не похожая на все остальные теории Парфенона, там, где оно есть, с большой точностью дает золотое сечение. Точные обмеры показывают, что в самом Парфеноне закон золотого сечения выполнен приблизительно.

(Для поклонников золотого сечения покажем, что в теории Шевелева таковое имеется и в чистом виде. Например, отношение а₁ :(a₂ + a₅) = l:2k₁ = (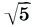 + 2):2 = Φ. Этот факт еще раз говорит только о том, что двойной квадрат 1: 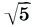тесно связан с золотым сечением.)

Прежде чем окончательно расстаться с Парфеноном, заметим, что и пропорции этого шедевра, и дорический ордер, в котором он выполнен, были не единственными архитектурными канонами, созданными гениальными древними греками. Неподалеку от Парфенона, на том же священном для древних и для современной цивилизации Акрополе, возвышается и другой бессмертный шедевр - храм Афины и Посейдона-Эрехтея - Эрехтейон, построенный чуть позже Парфенона, в 421 - 406 гг. до н. э. Но как не похоже это изящное и изысканное асимметричное сооружение, исполненное в ионическом ордере, на спокойный, строгий и симметрично уравновешенный Парфенон! Сколь отличны их пропорции! Достаточно сказать, что колонны Эрехтейона "вдвое стройнее": в них отношение диаметра основания к высоте равно 1:10. Но пропорции Эрехтейона - это еще одна увлекательная страница в архитектуре античности. А нас уже ждут гулкие своды готики.

Из светлого и жизнеобильного мира Древней Эллады перенесемся сквозь полтора тысячелетия в сумрачную эпоху европейского средневековья. Как все переменилось! Иная культура, иная философия, иная религия, иная архитектура... Вместо озаренной улыбкой античной любви к жизни и человеку - философия "умерщвления плоти", презрения земных радостей, аскетизма. Любые ростки свободной мысли, всякий вольный полет фантазии проходили через безжалостное прокрустово ложе церковных канонов. Но и в этих условиях

Дух знанья жил, скрыт в тайном 
эликсире, 
Поя целебно мутный мрак веков. 
.............................
Искал алхимик камень мудрецов, 
Ум утончался в преньях о вампире, 
Познать творца пытался богослов,- 
И мысль качала мировые гири.

(В. Брюсов)

"В те времена каждый родившийся поэтом становился зодчим. Рассеянные в массах дарования, придавленные со всех сторон феодализмом... не видя иного исхода, кроме зодчества, открывали себе дорогу с помощью этого искусства, и их илиады выливались в форму соборов. Все прочие искусства повиновались зодчеству и подчинялись его требованиям... Архитектор - поэт - мастер в себе одном объединял скульптуру, покрывающую резьбой созданные им фасады, и живопись, расцвечивающую его витражи, и музыку, приводящую в движение колокола и гудящую в органных трубах. Даже бедная поэзия, подлинная поэзия, столь упорно прозябавшая в рукописях, вынуждена была под формой гимна или хорала заключить себя в оправу здания..." (В. Гюго. "Собор Парижской Богоматери").

Но если греческое сознание всегда было обращено к человеку, если даже в дорических колоннах греки видели торжественное могущество мужского тела, а в изящных завитках ионических волют - женскую грацию и кокетство, то ни о каких реминисценциях с пропорциями человеческого тела в готической архитектуре не могло быть и речи. Человеческая плоть презиралась христианской религией, и в пропорциях готики господствует холодная геометрия. Треугольники и квадраты - простейшие геометрические фигуры - вот основа готических пропорций; триангулирование и квадрирование^* - вот методы достижения гармонии в готике. Но ведь и чистая геометрия прекрасна, и она смогла стать теоретической базой готической архитектуры, которая, по словам Гоголя, "есть явление такое, какого еще никогда не производил вкус и воображение человека".

^* (Триангулирование и квадрирование - методы геометрических построений, в основе которых лежат треугольники (лат. triangulum) или четырехугольники (лат. guadratus) и, в частности, квадраты.)

Хотя средневековье на полтора тысячелетия ближе к нам, чем Древняя Греция, мы также почти не располагаем подлинными документами о методах строительства готических соборов. И причиной тому не столько пламя военных пожарищ, беспрерывно полыхавшее над Европой, сколько особый характер созданных средневековыми строителями и зодчими организаций. Это были не просто обычные для средневековья цеховые объединения. Это были союзы, именовавшие себя братствами строителей-каменщиков, которые, подобно пифагорейским союзам, были окружены плотной завесой тайны. Члены братства каменщиков считали себя избранными, приобщенными к тайнам высочайшего искусства архитектуры. Как и пифагорейцы, каменщики пользовались лишь им понятным символическим языком, тщательно оберегая от непосвященных свои профессиональные секреты. И если у пифагорейцев их главной богиней была математика, то средневековые каменщики боготворили архитектуру. Собрания членов братства происходили в закрытых помещениях - ложах. Ложи имели строгую иерархию, разделяя братьев на учеников, подмастерьев, мастеров, великих мастеров. Вступая в ложу, ученики приносили клятву верности братству и соблюдения тайны великого искусства архитектуры. Собрания и прием новых членов регламентировались строго разработанным церемониалом, до краев наполненным средневековым мистицизмом. Все это свидетельствует об исключительном авторитете науки и искусства архитектуры в средние века. Заметим, что под влиянием союзов каменщиков-строителей средневековья с начала XVIII века в Европе возникают религиозно-этические союзы вольных каменщиков-масонов (от франц. macon - каменщик). Ложи масонов, сохранившие на Западе огромное влияние и поныне, уже не имели никакого отношения к строительству, хотя и заимствовали у своих средневековых предшественников полный набор мистических обрядов и традиций. (Собрание масонской ложи красочно описано в "Войне и мире" Льва Толстого.)

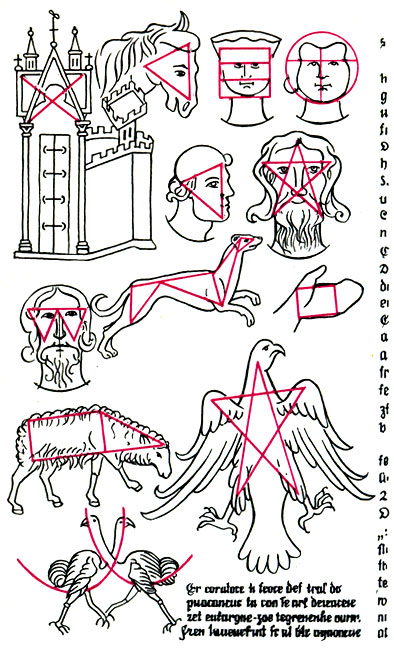
Виллар де Оннекур. Рисунки из альбома. 1235. Париж. Национальная библиотека. Попытки геометризированного рисования человека и животных, приведшие к полному отрицанию естественных пропорций

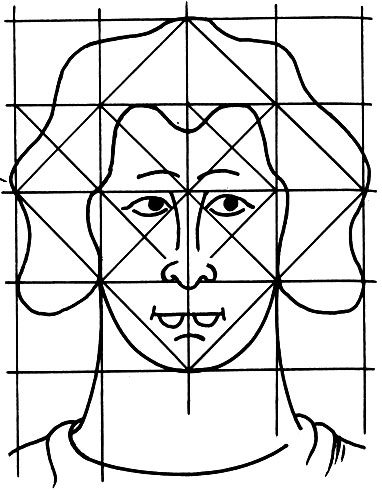
Виллар де Оннекур. Рисунки из альбома. 1235. Париж. Национальная библиотека. Попытки геометризированного рисования человека

Но истину нельзя удержать в узде: стало достоянием человечества учение Пифагора, обрели жизнь и теоретические изыскания мастеров-каменотесов. Наиболее ранние из них мы находим в альбоме французского зодчего XIII века Вил л ара де Оннекура. Альбом содержит ряд геометрических конструкций, позволявших моделировать архитектурные формы, а также размышления автора о пропорциях человеческого тела. Сколь отличны эти рисунки от работ античных мастеров! Если древние греки пытались постичь законы пропорционального строения человеческого тела, а затем перенести эти законы на архитектурные сооружения, то средневековые мастера, наоборот, пытаются втиснуть живые линии в рамки простейших геометрических фигур, полностью игнорируя естественные пропорции. Вот голова мужчины, вписанная в сетку квадратов и их диагоналей (см. рис.). Это отнюдь не шарж или шутка, а прорисовка с витражей знаменитого Реймского собора. Человеческое тело не является более "мерой всех вещей". Такой мерой становится система геометрических фигур. Именно сетка геометрических линий является тем скелетом, на котором строится тело здания.

К концу XV века было издано несколько книг, посвященных секретам строительного мастерства средневековых зодчих. Вот строки из книги "О камне", написанной в 1486 г. немецким мастером Матхаусом Роцирером: "Если хочешь начертить план башни на точной геометрической основе по примеру каменотесов, начерти квадрат, обозначь его углы буквами а, Ь, с, d ... затем раздели линию а - b на две равные части и обозначь середину буквой е и таким же образом раздели три оставшиеся стороны квадрата. Затем поверни меньший квадрат так, как показано на рисунке". Система квадратов, описанная здесь, очевидна.

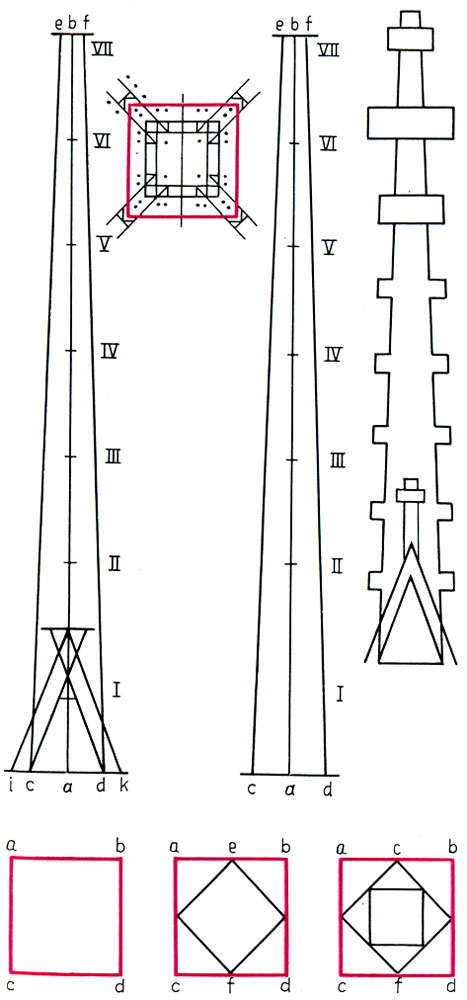
Чертежи для конструирования готических башен из книги Матхауса Роцирера 'О камне'. Регенсбург. 1486 (а)

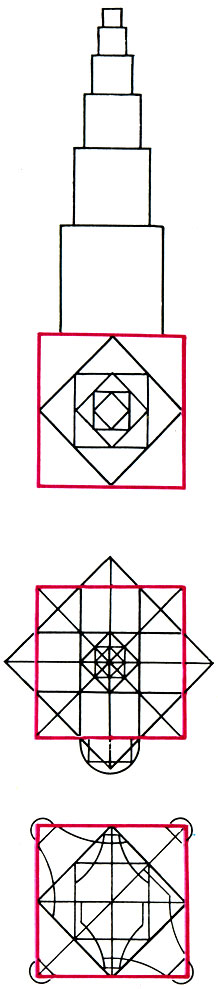
Система квадрирования из книги Лоренца Лахера 'Наставления мастера Лахера'. Нюрнберг. 1516 (б)

Система триангулирования Миланского собора. Иллюстрация из 'Комментариев к Витрувию' Цезаря Чезарино. Милан. 1521

Миланский собор. 1386-1858. Этот самый большой из всех готических соборов мира вмещает 40 000 молящихся. Строительство собора началось в 1386, шпиль был сооружен в 1756-1779, главный фасад завершен в 1805-1813, а последний шпиль - в 1858. Таким образом, собор строился 572 года!

Витражи королевской капеллы Сен-Шапель-жемчужины французской высокой готики. Париж. 1240-1248

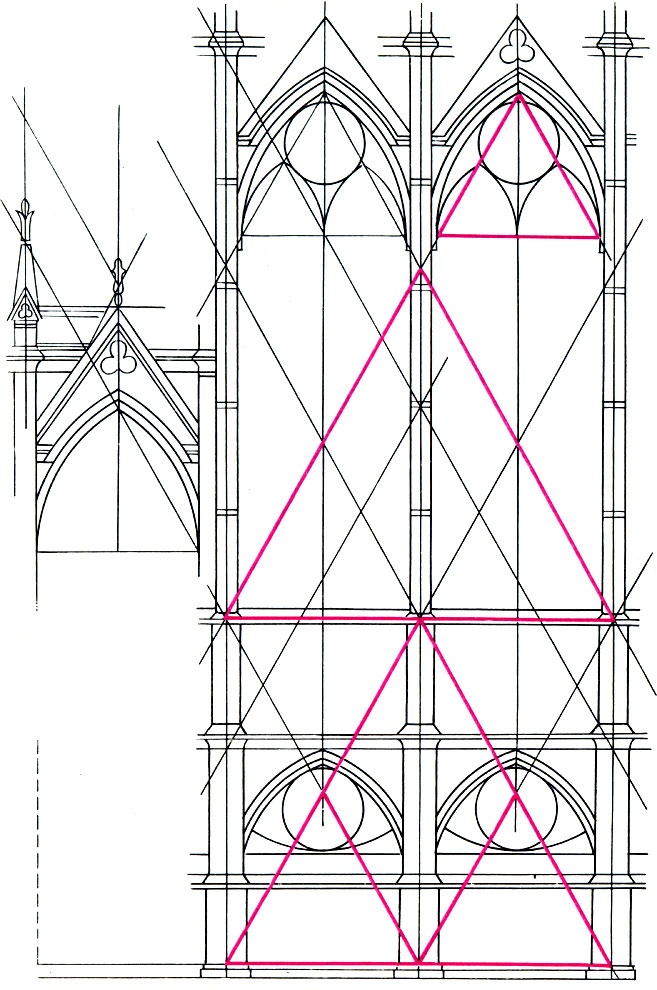
Равносторонний треугольник - основа пропорциональной сетки капеллы Сен-Шапель (по Виолле-ле-Дюку)

Однако протест всесильных лож, требовавших строжайшего запрета на разглашение тайн строительства, помешал Роциреру продолжить публикацию своих трудов. Более того, из сохранившихся документов известно, что за нежелание подчиняться уставу строитель собора мастер Вольфган Роцирер, дядя Матхауса Роцирера, а с ним и резчик Микаэл Лой в 1514 г. были приговорены к смертной казни.

Пропорции западного фасада собора Парижской Богоматери

Показательны и строки из завещания сыну другого немецкого мастера Лоренца Лахера, написанного в 1516 г.: "Впиши один в другой три квадрата - и ты получишь длину и ширину, это та единая основа, к которой сводятся почти все необходимые нам чертежи".

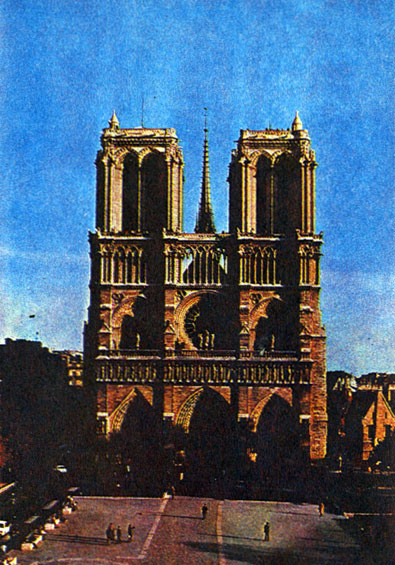
Собор Парижской Богоматери (Нотр-Дам де Пари). Западный фасад. 1163-1257

Но была у средневековых мастеров и другая система пропорционального построения - система триангулирования. Противоположность мнений сторонников систем "ад квадратум" и "ад триангулам" со всей остротой проявилась в дискуссии, состоявшейся во время строительства Миланского собора. По причине огромных размеров собора, заложенного в 1386 г., при его строительстве возникли серьезные затруднения. Миланские зодчие пригласили иностранных коллег. В 1389 г. из Парижа был вызван мастер Николас де Бонавентура. В 1391 г. миланский мастер Джиованни был направлен для консультаций в Германию к мастеру Кельнского собора. В 1394 г. из германского города Ульма прибыл в Милан Ульрих фон Энсинген, а в 1399 г.- из Парижа Жан Миньо. В этот период положение с собором стало критическим. 11 января 1400 г. состоялось собрание всех архитекторов, на котором возник серьезный спор между Миньо и итальянскими зодчими. Разногласия во мнениях составили 54 пункта, среди которых был и пункт о системах пропорционирования. Сторонники системы триангулирования победили. На чертеже, сделанном в 1521 г. Чезаре Чезарино с оригинала 1395 г., мы видим, что в основе пропорций собора лежат равносторонние треугольники (см. рис. на с. 230).

Пропорции: от Парфенона до Нотр-Дама

Среди сторонников системы триангулирования также велись споры относительно того, из каких треугольников должна состоять пропорциональная сетка готического собора: равносторонних, "египетских" и т. д. Мы не будем углубляться в эти теоретические премудрости, а только заметим, что и сторонники системы "ад триангулам", и приверженцы схемы "ад квадратум" оставили потомкам первоклассные архитектурные памятники. В качестве примера укажем на две жемчужины французской столицы: королевскую капеллу Сен Шапель (1243-1248) и знаменитый Нотр-Дам де Пари - собор Парижской Богоматери (1163-1257).

Капелла Сен Шапель - вершина высокой готики, образец совершенной гармонии и безукоризненной формы. Интерьер капеллы ошеломляет даже знатоков готического искусства: потоки теплого света, струящиеся из ее витражей, мощным аккордом вливаются в застывшую симфонию изысканных архитектурных форм капеллы. Согласно исследованиям Виолле-ле-Дюка, пропорциональная сетка капеллы построена на равносторонних треугольниках.

Собор Парижской Богоматери - самый величественный и самый популярный памятник ранней готики. В гордой размеренности западного фасада собора горизонтальные линии еще соперничают с вертикальными. Еще не исчезла стена фасада (ведь это только начало готики), но она уже приобрела легкость и даже прозрачность. Как показал французский историк архитектуры Огюст Шуази, пропорциональную основу западного фасада собора Нотр-Дам составляет квадрат, а высота башен фасада равна половине стороны этого квадрата...

Но чем внимательней, твердыня 
Notre-Dame, 
Я изучал твои чудовищные ребра, 
Тем чаще думал я: "Из тяжести 
недоброй 
И я когда-нибудь прекрасное 
создам..." 

(О. Мандельштам)