
18. Архитектура - математика - музыка
Вообще архитектура есть застывшая музыка.
Один благородный философ говорил о зодчестве как о застывшей музыке и за то не раз подвергался насмешкам. Мы думаем, что мы лучше всего передадим эту прекрасную мысль, назвав архитектуру отзвучавшей мелодией.
С легкой руки великого Гёте афоризм об архитектуре и музыке немецкого философа, идейного вождя немецкого романтизма Фридриха Шеллинга (1775-1854) стал настолько популярным, что сегодня, забыв имя настоящего автора, его настойчиво вкладывают в уста создателя "Фауста". Парадоксальность высказывания Шеллинга, соединившего в себе две столь далекие друг от друга области искусства - архитектуру и музыку, делает его еще более привлекательным. А ведь сопоставление архитектуры и музыки в большей степени закономерно, чем парадоксально, и поистине замечательно, что связующим звеном между архитектурой и музыкой выступает математика.

Гравюра из книги Франкино Гафурио 'Теория музыки'. Мы видим атрибуты музыки - органные трубы и струны, связанные отношениями 6:4:3, а также атрибут архитектуры - циркуль, который, возможно, указывает на применение этих отношений в архитектуре
В чем же проявляется общность архитектуры, музыки и математики? Прежде всего - в максимальной абстрактности этих форм человеческой деятельности. Архитектура является наиболее абстрактным из пластических искусств, т. е. искусств, существующих в пространстве и воспринимаемых зрением. Назначение зрения - воспринимать предметы внешнего мира, а назначение пластических искусств - воспроизводить с той или иной мерой чувственной достоверности эти предметы. Однако архитектура не отображает реально существующие объекты, а создает некоторые абстрактные формы, которые являются плодом фантазии ее творца. Конечно, нам известны колонны в форме лотоса в древнеегипетской архитектуре или древнегреческие атланты и кариатиды, растительные мотивы коринфских капителей или звериные маски во владимиро-суздальском зодчестве. Но все это лишь элементы, украшения, архитектурная скульптура, но не сама архитектура в целом.
Музыка на первый взгляд является антиподом архитектуры. В противоположность архитектуре музыка развивается во времени, а не в пространстве; музыка обращена к слуху. Однако роднит эти два искусства та же абстрактность формы. В самом деле, на слух мы воспринимаем звуковую информацию из внешнего мира. Но музыка не воспроизводит словесную речь, она ничего не описывает и обычно не изображает природные звуки и звукосочетания. Музыкальная форма абстрактна, она рождается в голове ее создателя и практически не имеет аналогов во внешнем мире.
Так же и математика. Будучи наукой, целью которой является выработка и систематизация объективных знаний о действительности, математика не имеет' материального предмета изучения во внешнем мире. Математика - предельно абстрактная наука, но именно это качество наделяет ее силой, позволяет математике стать универсальным языком науки. Впрочем, эти качества математики мы уже обсуждали в главе 2.
Как и математика, архитектура и музыка от объектов реального мира через многие ступени абстракции поднимаются до совершенных высочайших идеальных образов. И разница между этими сферами творческой деятельности здесь проявляется лишь в том, что в математике абстрактные образы логические, в музыке - чувственные, а в архитектуре, пожалуй, и те и другие, ибо архитектура вбирает в себя качества и науки, и искусства. Ни математик, ни композитор, ни архитектор не могут непосредственно сравнить результаты своего творчества с конкретными явлениями внешнего мира. И лишь одна путеводная звезда - логика развития науки или искусства - направляет их путь. Но разумеется, ни архитектурные, ни музыкальные, ни математические абстракции - это не химеры, существующие в своем ирреальном мире, а те идеализации, которые, отбрасывая преходящее, частное, отражают природу глубже, вернее, полнее.
Итак, архитектура и музыка являются искусствами неизобразительными и неописательными. Архитектурная и музыкальная формы абстрактны, и поэтому в них яснее, нежели в других искусствах, проявляются такие законы построения формы, как симметрия, пропорциональность, гармония, равенство, повторы частей и т. д. Лишенные внутренних законов построения, эти абстрактные формы будут лишены и тех внешних ориентиров, которые так необходимы при их восприятии. Именно объективным системным характером внутренних законов построения музыкальной формы объясняется то, что "музыка вызывает сходные мысли в разных головах" (Бодлер). То же в полной мере относится и к архитектуре.
Но откуда и архитектуре, и музыке взять законы построения формы, "законы красоты", которые бы стали их фундаментом? Для тех, кто стоит на "природнической" точке зрения на красоту, этой проблемы не существует. Разумеется, у природы. Но ведь законы природы, законы гармоничного, целесообразного и прекрасного устройства мироздания описываются математикой! Вспомним "непостижимую эффективность математики в естественных науках" (с. 44), вспомним слова Гейзенберга: "Понимание всего богато окрашенного многообразия явлений достигается путем осознания присущего всем явлениям объединяющего принципа форм, выражаемого на языке математики. Таким же образом устанавливается тесная взаимосвязь между тем, что воспринимается как прекрасное, и тем, что доступно пониманию лишь с помощью интеллекта".
Особенно ценно, что к тому же выводу о необходимости существования в основе архитектуры и музыки "объединяющего принципа формы" приходят не только представители естественных наук (что вполне естественно), но и служители мира искусств. Вот слова архитектора, академика Щусева: "Наряду с меняющимися формами природы и жизни есть и нечто вечное, а именно - закон красоты и гармонии, который проявляется одинаково в жизни природы и человека. Именно этот закон дает возможность построить теорию пропорций и пластических форм, а в музыке - теорию соотношения звуковых ладов". А вот мнение музыковеда, профессора Мазеля: "Без высотной (ладовой) организации музыки невозможно выработать некоторый "музыкальный язык", понятный широкому кругу людей. Без какой-либо ладовой системы, существующей во внутреннем слухе поющих, напев не мог бы запомниться и передаваться".
Но что же является этим загадочным "объединяющим принципом формы", который должен лежать в основе архитектуры и музыки? Как нам кажется, именно математика стала тем фундаментом, тем "законом красоты и гармонии", на котором строятся абстрактные формы архитектуры и музыки.
Поясним эту мысль на знакомых нам примерах. В главе 11 мы задавались вопросом: почему из 4000 звуков, хорошо различимых человеком, в музыке используются лишь около 90? Да только потому, что в основу музыки положена строгая математическая организация звуков. Только организовав звуки в октавы, только упорядочив их внутри каждой октавы, человек смог навести в мире звуков порядок, который стал "радовать глаз и разум" (в нашем случае - "слух и разум"). Только после построения гаммы стало возможным выработать "музыкальный язык" и передавать "музыкальные мысли" - мелодии на этом языке. Таким образом, музыкальная гамма - это основа музыкального языка, заложенная по законам математики. Ну а что сказать на этом языке, зависит от таланта, вкуса, душевного богатства композитора.
Что представляет собой гамма внутри октавы, каково ее математическое строение? Этим вопросом мы занимались практически на протяжении всей второй части. В главе 9 мы показали, что равномерно-темперированная гамма - основа сегодняшней музыки - есть не что иное, как геометрическая прогрессия со знаменателем 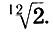 Но ведь именно в геометрической прогрессии достигается соразмерность частей и целого, именуемая гармонией. Таким образом, гамма в пределах октавы также есть упорядоченная по законам математики последовательность звуков, которая в силу октавного подобия звуков является основой основ музыки. Не случайно Пифагор придавал огромное значение построению именно этой части музыкальной шкалы (см. эпиграф к гл. 6).
Но ведь именно в геометрической прогрессии достигается соразмерность частей и целого, именуемая гармонией. Таким образом, гамма в пределах октавы также есть упорядоченная по законам математики последовательность звуков, которая в силу октавного подобия звуков является основой основ музыки. Не случайно Пифагор придавал огромное значение построению именно этой части музыкальной шкалы (см. эпиграф к гл. 6).
То же самое мы наблюдаем и в архитектуре. Из бесконечного многообразия соотношений между частями и целым в архитектурных шедеврах непременно заложена какая-то математическая закономерность, позволяющая отобрать и упорядочить эти отношения. В основе построения архитектурной формы лежит некоторый математический закон - закон пропорционального строения этой формы. В качестве такого закона в силу особых математических свойств (см. гл. 15) часто выступает геометрическая прогрессия - ряд золотого сечения или его производная - модулор Ле Корбюзье, а также функция золотого сечения или парные меры 1:√2 или 1:√5 Эти математические закономерности гармонизируют размеры сооружения, определяют его соразмерную структуру. Разумеется, как в музыке, так и в архитектуре пропорциональная шкала - это только "эстетический фундамент" архитектурного произведения, который никак не сдерживает творческой фантазии автора.
Заметим, что проблема гармонизации частей и целого давно уже перестала быть прерогативой лишь музыки или архитектуры. Повышение эстетических качеств промышленных изделий, придание им красивой формы и одновременно их стандартизация - одна из важнейших задач технической эстетики. Естественно, что решается эта задача на базе того же математического аппарата.
Чтобы связать части целого единым пропорциональным отношением, строятся так называемые ряды предпочтительных чисел (R), которые являются не чем иным, как геометрическими прогрессиями. В качестве знаменателей таких прогрессий выбирают степени числа 10. При этом сами степени в свою очередь образуют геометрическую прогрессию со знаменателем: 1/2: 1/5, 1/10, 1/20, 1/40. Так получаются инвариантные гармонические ряды:
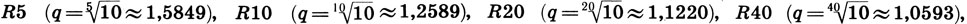
что каждый предыдущий ряд "вложен" во все последующие. Кроме того, поскольку 103/10 = 106/20 = 1012/40 = 1,9951≈2, то в ряду R10 происходит удвоение чисел через каждые 3 члена, в ряду R20 - через 6 членов, а в ряду R40 - через 12 членов. Исходя из этого свойства значения предпочтительных чисел " округляются.
Отметим одну любопытную деталь. Так как 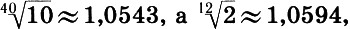 то с достаточной степенью точности можно сказать, что ряд R40 лежит в основе равномерно-темперированного строя:
то с достаточной степенью точности можно сказать, что ряд R40 лежит в основе равномерно-темперированного строя:

Преимущества гармонизации с помощью ряда предпочтительных чисел (геометрической прогрессии) перед обычным рядом чисел (арифметической прогрессией) очевидны из простого примера. Если стороны прямоугольника а и b увеличивать в геометрической прогрессии (аn = aqn, bn = bqn), то пропорции прямоугольника будут сохраняться: 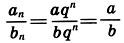 более того,
более того, 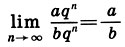 Арифметическая прогрессия (an = a + nq, b = a + nq) не сохраняет пропорции прямоугольника:
Арифметическая прогрессия (an = a + nq, b = a + nq) не сохраняет пропорции прямоугольника: 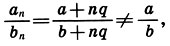 , причем
, причем 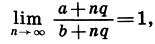 т. е. форма прямоугольника будет приближаться к квадрату. Свойство геометрической прогрессии сохранять пропорции ее членов было использовано еще в 1805 г. во Франции для упорядочения типографских шрифтов.
т. е. форма прямоугольника будет приближаться к квадрату. Свойство геометрической прогрессии сохранять пропорции ее членов было использовано еще в 1805 г. во Франции для упорядочения типографских шрифтов.
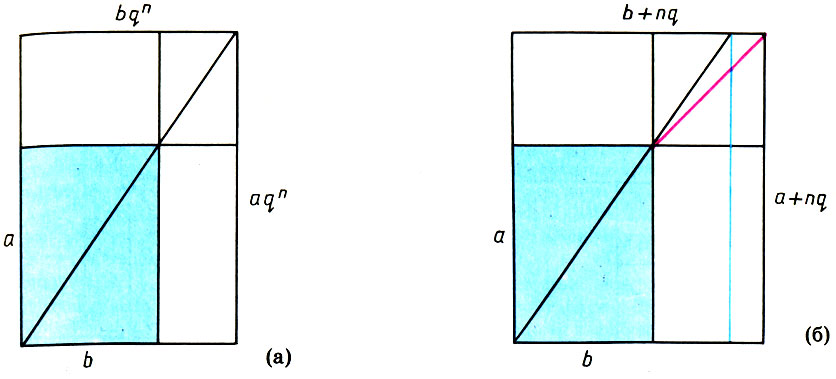
Изменение сторон прямоугольника с помощью геометрической прогрессии сохраняет его пропорции (а), а с помощью арифметической прогрессии искажает их (б)
Отметим еще одну геометрическую прогрессию, имеющую непосредственное отношение к этой книге. Сегодня во многих странах, в том числе и в нашей, применяется стандарт, введенный в начале века немецким ученым Портсманом. Портсман выбрал отношение сторон прямоугольного листа бумаги а:b из условия, чтобы при складывании (фальцовке) эта пропорция сохранялась, т. е. a:b = b:a/2 (см. рис.). Решая это элементарное уравнение, находим: а:b = √2. В качестве исходного формата был выбран лист площадью 1 м2 со сторонами 1189X841 мм (√:1), а затем найдены и его доли: 1/2 м2 = 841Х594 мм; 1/4 м2 = 594Х Х420 мм; 1/8 м2 = 420Х297 мм; 1/16 м2 = 297X210 мм - лист для пишущей машинки; 1/32 м2 = 210X148 мм; 1/64 м2 = 148X105 мм - формат почтовой открытки. Так был построен основной ряд форматов бумаги RA. Существуют также и производные от этого ряда.
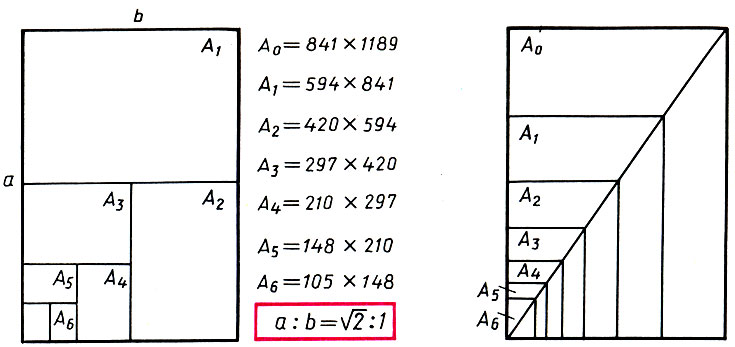
Построение основного формата бумаги RA с помощью геометрической прогрессии (q = √2), сохраняющей пропорции прямоугольного листа при фальцовке
Как видим, математические вопросы гармонизации частей и целого увели нас далеко и от музыки, и от архитектуры. Как тут не вспомнить высказывание английского естествоиспытателя, соратника Чарльза Дарвина - Томаса Гексли (1825-1895) о том, что математика, подобно жернову, перемалывает то, что под него засыпают. Однако если вдуматься, то все это имеет самое прямое отношение к нашей теме, ибо как на стандартном листе бумаги можно написать все что угодно, так и с помощью гармонизированной шкалы звуков (музыкальная гамма) или шкалы пропорций (модулор Ле Корбюзье) можно создать бессмертное произведение, а можно и...
Но вернемся к архитектуре и музыке. Музыка развивается во времени, она не стоит на месте, подвижна, она меняется каждое мгновение. Но если прозвучавшую музыку целиком охватить в памяти, то в нашем сознании станут проступать закономерности ее архитектурного строения: симметрия, пропорциональность, соразмерность частей и целого - гармония, ритм и т. д.
Именно законы общего построения музыки, которые выявляются памятью только в отзвучавшей мелодии, своеобразный глобальный ритм музыки и роднят ее с архитектурой. Именно "отзвучавшую музыку", ее глобальный ритм, ее архитектуру мы изучали в главе 12, когда рассматривали целиком всю хроматическую фантазию и всю фугу ре минор Баха и находили в их строении, в больших и малых формах пропорции золотого сечения, законы симметрии (см. с. 164).
С другой стороны, локальный ритм музыки, звучащие сию минуту музыкальные фразы сближают музыку с поэзией. И как связь музыкального произведения с поэтическим словом или сценическим действием делает образное содержание произведения более богатым и многогранным, так и связь произведения архитектуры с пластикой скульптуры и живописи (росписи стен, мозаики, барельефы, скульптурные группы) - синтез искусств - позволяет достигнуть многостороннего эмоционального воздействия, небывалого по силе и полноте чувств.
Архитектура во времени неизменна. Но подвижен человек, и, перемещаясь, он воспринимает архитектуру динамично. Меняя свое положение в архитектурной среде, глядя на памятник архитектуры с разных точек зрения, человек по-разному воспринимает его пластические формы; они оживают, и "застывшая музыка" начинает издавать волшебные звуки. "Искусство архитектуры заключается в том, чтобы заставить звучать опоры",- говорил французский архитектор О. Перре. Мысль эта отнюдь не парадоксальна: опора, несущая тяжесть, была и остается главной темой архитектурной симфонии, как вечен сам закон тяготения.
Но архитектура динамична даже тогда, когда воспринимающий ее человек неподвижен. Меняется положение солнца, и изменяется светотеневая пластика архитектурных форм. Днем и ночью, в предрассветном тумане и в лучах заходящего солнца, укутанные мягким снегом и омытые грозовыми дождями памятники зодчества поют неповторимые чарующие песнопения.
Итак, неподвижная архитектура, подобно звучащей музыке, постигается нами во времени. Однако процессы восприятия архитектуры и музыки существенно отличаются друг от друга. Музыка, как и само время, развивается только в одном направлении; ее нельзя повернуть вспять, остановить или ускорить по воле слушателя. Напротив, при рассмотрении памятника архитектуры мы не связаны никакой наперед заданной последовательностью, мы вольны приблизиться к архитектурному сооружению или отойти от него, зайти слева и справа, остановиться. Поэтому в музыке композитор имеет возможность управлять процессом эстетического восприятия, он может заранее подготовить слушателя к кульминации или для усиления выразительности допустить диссонанс и тут же разрешить его в консонанс.
Архитектор лишен таких возможностей. Архитектурный диссонанс не может организованно разрешиться в консонанс и будет постоянно довлеть на зрителя. В отличие от музыки, которая может быть веселой и задумчивой, торжественной и траурной, архитектура - это искусственная среда, в которой человеку предстоит жить и работать, и она должна доставлять ему только радость. Правда, есть и обратные примеры. Стендаль признавался: "Я бы разучился смеяться через неделю, если бы жил в палаццо Арконати". Немало унылых памятников архитектурной какофонии окружают нас и сегодня. И все-таки по своей эстетической направленности архитектура призвана быть искусством положительных эмоций, она должна вбирать в себя все лучшие духовные ценности человечества и нести их людям. "Архитектура включает в себя всю культуру эпохи, в архитектуре проявляется дух времени",- писал Ле Корбюзье, чье высказывание дополняют слова Луначарского: "Всякому великому времени соответствует великая архитектура".
Есть в архитектуре и еще одно движение - внутреннее. Оно несет в себе один из парадоксов искусства архитектуры - движение, застывшее в вечном покое. В дорических колоннах Парфенона чувствуется невозмутимая и величавая поступь героя, а в ионическом ордере Эрехтейона - легкий шаг античной красавицы. В готике все устремлено вверх: на головокружительную высоту взлетают пучки тонких нервюр и распадаются там в паутину сводов, тянутся вверх стрельчатые окна витражей, зубчатые шпили и башенки. Среди зелени лесов и полей кружится хоровод древнерусских церквей...
Так неподвижная архитектура оживает при ее восприятии, а подвижная музыка застывает в нашей памяти.
И в заключение - немного истории, ибо сопоставление архитектуры и музыки имеет давнюю традицию и началось задолго до Шеллинга и Гёте. o Как музыка в античную эпоху считалась дочерью математики, так и архитектура мыслителям Возрождения казалась дочерью музыки.
Ренессанс... Новая весна человечества... Возрождался интерес к античному духовному наследию, живой античной мысли и жизнеобильному античному искусству, бесплодные штудии божественного (studio divina) сменялись пытливым изучением человеческого (studio humana)...
Стремились все - открыть, изобрести, Найти, создать... Царила в эти годы Надежда - вскрыть все таинства природы.

Пифагор (справа), аллегория Арифметики и Боэций. Гравюра из книги Грегора Райха 'Маргарита философика'. В средневековой Европе Пифагор считался изобретателем счетной доски абака, а Боэций - создателем новой нумерации
Мы знаем (гл. 14) о том, какое огромное влияние на зодчих Возрождения оказал трактат Витрувия "Десять книг об архитектуре". Но мы также знаем, что архитектурная энциклопедия Витрувия стала источником многих заблуждений, происходивших чаще всего от неправильного толкования мыслей автора. Так случилось с архитектурой и музыкой.
Ссылаясь на авторитет Витрувия, архитекторы Возрождения выдвинули тезис о том, что наиболее приятными для созерцания должны быть те прямоугольники, стороны которых относятся как числа в благозвучных (консонантных) интервалах, т. е. как октава 2:1, квинта 3:2, кварта 4:3, а также большая 5:4 и малая 6:5 терции и их обращения - малая 8:5 и большая 5:3 сексты. В 1485 г. во Флоренции был издан трактат "Десять книг о зодчестве". Его автором был славный представитель архитектуры Раннего Возрождения, итальянский ученый, писатель и музыкант Леон Баттиста Альберти, умерший за 13 лет до того, как его детище увидело свет. "Десять книг" Альберти было вторым после "Десяти книг" Витрувия всеобъемлющим сочинением по архитектуре. В нем мы читаем: "И конечно, вновь и вновь следует повторить изречение Пифагора: "нет сомнений, что природа во всем остается себе подобной". Дело обстоит так: существуют числа, благодаря которым гармония звуков пленяет слух, эти же числа преисполняют и глаза, и дух чудесным наслаждением. Мы должны воспользоваться пропорциями, взятыми у музыкантов, кои величайшие мастера в этом виде чисел". Поскольку приятные слуху музыкальные интервалы описываются отношением целых чисел, то, согласно Альберти, и приятные глазу архитектурные формы также должны находиться в целочисленных "музыкальных" пропорциях.
В XVI веке архитектора Альберти поддержал математик Джероламо Кардано (1501 -1576), известный сегодня как автор формулы решения кубичного уравнения, которую, впрочем, как великую тайну ему открыл Никколо Тарталья (ок. 1499 - 1557). Как истинный представитель точного знания Кардано утверждал, что приятные для слуха и глаза целочисленные (музыкальные) отношения являются таковыми, поскольку они легкопостижимы разумом. Авторство музыкальной аналогии в архитектуре Кардано также приписывал незыблемому авторитету Витрувия.
В действительности интерес Витрувия к музыке ограничивался вопросами конструирования резонаторов для античных театров, а также правильной настройкой струн в катапультах и боевых машинах, которые находились в ведении архитекторов того времени. Правда, Витрувий дал в качестве прекрасных пропорций три "музыкальных" отношения 2:1, 3:2, 5:3. Но наряду с ними он рассматривал и такое отнюдь не музыкальное отношение, как отношение диагонали к стороне квадрата √2:1.
Как бы то ни было, но музыкальная аналогия прочно вошла в сознание архитекторов Возрождения. На первый взгляд, кажется странным, что теоретические воззрения зодчих Возрождения в большей мере определялись не трудами самих архитекторов, а математическими разработками по теории музыки. Но если вдуматься, то это, скорее, следовало из универсального характера математики: хорошо известные в музыке "математические законы красоты" (законы целочисленных консонантных отношений и законы среднепропорциональных) архитекторы Возрождения пытались перенести на свою почву. Не говорит ли эта попытка "пройти" из музыки в архитектуру с помощью математики о безграничной вере мыслителей Возрождения в универсальное могущество математики?!
Огромную роль в развитии музыкальной аналогии в архитектуре сыграл трактат Северина Боэция "О музыке", который вобрал в себя все античные теории музыкальной гармонии и фактически сохранил их для потомков. Автор другого выдающегося трактата по математической теории музыки - итальянский композитор XVI века Джузеппе Царлино - нам также знаком. Как мы знаем (с. 129), среди современников-музыкантов идеи Царлино должного признания не получили. Зато математические выкладки Царлино и его мысль о том, что консонантные (приятные для слуха) интервалы получаются как среднее арифметическое и среднее гармоническое, запали в душу современников-архитекторов и применялись ими для получения "консонантных" (приятных для глаза) пропорций.

Палладио. Вилла Ротонда в Виченце. 1581. Воплощение идеи симметрии, математической строгости и музыкальных пропорций в архитектуре Ренессанса
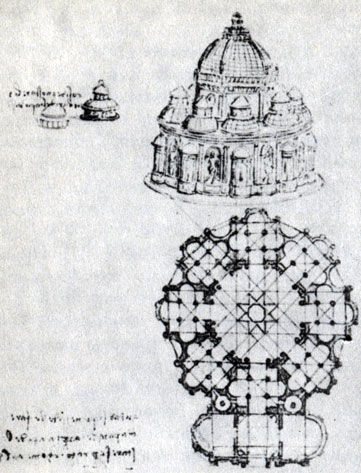
Леонардо да Винчи. План собора, основанный на правильной восьмиконечной звезде, обладает поворотной симметрией 8-го порядка и отнюдь 'не музыкальной' системой пропорций √2:1
Музыкальная система пропорционирования нашла живой отклик в творчестве выдающегося итальянского архитектора Андреа Палладио (1508 -1580)- автора трактата "Четыре книги об архитектуре". Созданные Палладио типы городского дворца, церкви, виллы благодаря своей завершенности, сочетанию строгой упорядоченности и пластики получили распространение не только в Италии XVI века, но и составили целое направление - палладианство - в европейском зодчестве XVII-XVIII веков. Идея всепроникающей музыкальной гармонии, структурно-математическое понимание красоты, идея симметрии как неотъемлемого качества красоты наиболее полно воплощены Палладио в вилле Ротонда. С высоты птичьего полета в этом каноне архитектуры Ренессанса хорошо видны как поворотная симметрия 4-го порядка всего здания, так и зеркальная симметрия его фасадов, а также ощущается музыка простых целочисленных пропорций.
Вообще, убеждение в том, что архитектура - это наука и что красота здания определяется симметрией и математическими законами гармонии, можно считать главной аксиомой архитектуры Возрождения. Мыслители Возрождения были неоплатониками. Они верили в то, что платонов гептахорд (7.1), который содержит все консонансы, определяет гармонию мироздания, а значит, и единую гармонию всех искусств, а значит, и архитектуры.
И все-таки Палладио был больше архитектором, нежели философом-неоплатоником. Именно поэтому Палладио включил прямоугольник, стороны которого равны стороне и диагонали квадрата, т. е. прямоугольник с иррациональным соотношением сторон √2:1, в список семи форм,
рекомендуемых для планирования комнат. А ведь одного этого прямоугольника достаточно для того, чтобы полностью разрушить музыкальную аналогию в архитектуре.
В самом деле, как мы помним, интервал тритона √2:1 является острейшим диссонансом в музыке и назывался "дьяволом в музыке". С другой стороны, мы знаем, насколько широко парная мера √2:1 применялась в архитектуре. Знали это и архитекторы Возрождения. И не только из сочинений Витрувия. Достаточно вспомнить проект собора, выполненный Леонардо да Винчи и основанный на последовательности восьмиконечных звезд. Разбиение окружности на 8 равных частей порождает угол в 45°, а восьмиконечная звезда - систему равнобедренных прямоугольных треугольников, т. е. треугольников с соотношением √2:1.
Таким образом, красота архитектурных форм явно не умещалась в прокрустово ложе целочисленных отношений. Это понимали архитекторы Позднего Возрождения, и это было для них такой же трагедией, какой открытие несоизмеримости было для их кумиров - пифагорейцев. "Можно сказать, что Ренессанс вообще раздирается этим ужасающим противоречием: возрожденцам хотелось видеть и изображать живое и одушевленное трехмерное тело и в то же самое время им хотелось все свести на арифметику целых чисел" (А. Лосев. "Эстетика Возрождения").
Тем не менее музыкальная аналогия в архитектуре оставалась очень популярной и продолжала жить в творчестве архитекторов-палладианцев XVII и XVIII веков. А попытки примирить музыку архитектуры с иррациональными отношениями не прекращаются и в XX веке. Так, одни исследователи пропорций обращают внимание на то, что золотое сечение Φ = 1,618... достаточно хорошо аппроксимируется (приближенно выражается) отношениями членов ряда Фибоначчи (15.6): 5/3-1,666... и 8/5-1,6 (это большая и малая сексты в музыкальной терминологии). Действительно, без наложения друг на друга эти три пропорции отличить практически невозможно, и, таким образом, с точки зрения эстетического восприятия споры о преимуществах той или иной пропорции кажутся академическими. Другие объясняют "приятность для глаза" диссонантных иррациональных отношений тем, что при восприятии архитектурной формы глаз соизмеряет не линейные размеры, а площади поверхности. Тогда два квадрата с "немузыкальным" отношением сторон √2:1 дают "музыкальное" отношение площадей 2:1 (октаву). Квадраты с немыслимым в музыке соотношением сторон √3:√2 дадут в площадях квинту 3:2 и т. д.
Мы не будем вдаваться в обсуждение вопроса, почему одни отношения приятны для слуха или для глаза, а другие - нет. Несмотря на давнюю историю, вопрос этот на карте науки остается почти абсолютно белым пятном. Напомним, что консонансы в музыке Гельмгольц объяснял отсутствием неприятных биений между обертонами составляющих их гармоник (см. с. 151). Однако в настоящее время в теории Гельмгольца обнаружено много изъянов и восприятие консонансов не считается чисто физиологическим явлением. Тем более нет каких-либо установившихся соображений для объяснения эстетики восприятия тех или иных пропорций. "Не углубляясь еще дальше в эту спорную область, хотелось бы подчеркнуть большое значение какой бы то ни было теории в архитектурном проектировании". Этими словами известный английский математик и знаток искусства Дан Пидоу в книге "Геометрия и искусство" закончил обсуждение проблемы эстетики восприятия музыкальных пропорций в архитектуре. Конечно, нам следовало бы внять его мудрому примеру, но хочется сказать еще два слова вот о чем.
В 1830-1834 гг. немецкий физиолог Эрнст Вебер (1795-1878) на основании многочисленных экспериментов установил, что человек воспринимает не абсолютный, а относительный прирост силы раздражителя (света, звука, груза, давящего на кожу, и т. д.), т. е. dR/R, где R - сила раздражителя, dR - прирост этой силы. Каждый по своему жизненному опыту знает, что, например, электрическая лампочка, включенная днем, не вызывает у нас никакой реакции, так как по отношению к солнечному свету прирост этой силы раздражения слишком мал(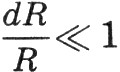 , так как R велико). Зато в темноте нас слепит даже зажженная спичка (здесь
, так как R велико). Зато в темноте нас слепит даже зажженная спичка (здесь 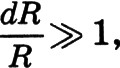 так как R≈0). R
так как R≈0). R
20 лет спустя немецкий физик, психолог, философ и писатель Густав Фехнер (1801 -1887) математически обработал результаты экспериментов Вебера, т. е. на языке математики записал факт, установленный Вебером: приращение интенсивности ощущения dE пропорционально относительному приращению силы раздраения dR/R
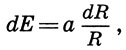 (18.1)
(18.1)здесь а - коэффициент пропорциональности. Получилось простейшее дифференциальное уравнение, решая которое Фехнер нашел связь между интенсивностью ощущения Е и силой раздражения R, действующей на какой-либо орган чувств:
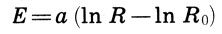 (18.2)
(18.2)или
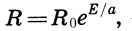 (18.3)
(18.3)здесь R0 - сила начального раздражения.
Формулы (18.1) - (18.3) и есть математическое выражение основного психофизического закона - закона Вебера - Фехнера.
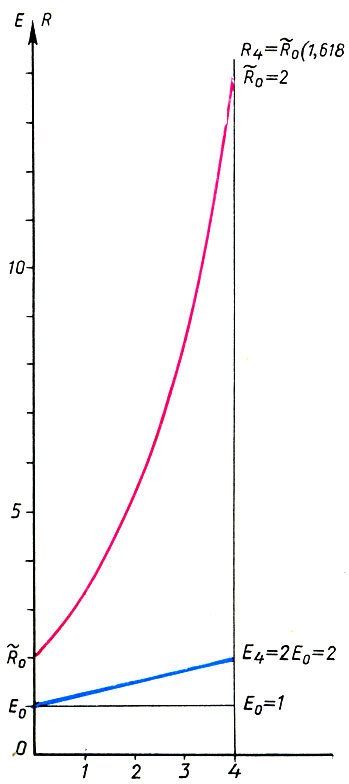
Согласно закону Вебера - Фехнера, для того, чтобы интенсивность ощущений Е нарастала в арифметической прогрессии, вызывающая их сила раздражения R должна нарастать в геометрической прогрессии
Что же мы можем извлечь из закона Вебера - Фехнера? Естественно предположить, что нам будет приятно, если наши ощущения в процессе восприятия музыки или архитектуры будут нарастать равномерно, т. е. в арифметической прогрессии. Положим Еn = Е0 + αn (n = 0, 1, 2, ...; α - разность арифметической прогрессии). Тогда согласно (18.3) вызывающая эти ощущения сила раздражения должна нарастать по закону
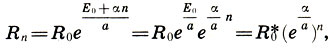
т. е. сила раздражения Rn должна нарастать в геометрической прогрессии со знаменателем q = eα/a.
Но ведь и гамма равномерно-темперированного строя (9.1), и ряд золотого сечения (15.4) или (15.5), и красная (17.2) и синяя (17.3) шкалы модулора Ле Корбюзье являются геометрическими прогрессиями! Следовательно, все эти "раздражители"- наших органов чувств обеспечивают равномерное возрастание (или убывание) наших ощущений. Таким образом, именно закон Вебера - Фехнера, скорее всего, и является тем математическим законом, который лежит в основе основ как музыки (музыкальная гамма), так и архитектуры (шкала пропорциональностей), той "математикой", которая связывает и музыку, и архитектуру!
Подтверждением этому могли бы стать экспериментальные значения коэффициента α/а, полученные в результате психофизических опытов. Поскольку для равномерно-темперированной гаммы q = = 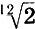 = 1,06, а для ряда золотого сечения q = 1,618 (q = eα/a), то легко находим: для музыкальной гаммы α/а = 0,058, а для ряда золотого сечения α/а = 0,482. Если эти значения совпадут с экспериментальными, то это и будет хотя бы в первом приближении объяснением, почему именно 12-ступенная гамма и золотое сечение в течение тысячелетий продолжают радовать наши слух, глаз и разум.
= 1,06, а для ряда золотого сечения q = 1,618 (q = eα/a), то легко находим: для музыкальной гаммы α/а = 0,058, а для ряда золотого сечения α/а = 0,482. Если эти значения совпадут с экспериментальными, то это и будет хотя бы в первом приближении объяснением, почему именно 12-ступенная гамма и золотое сечение в течение тысячелетий продолжают радовать наши слух, глаз и разум.
Насколько это справедливо, покажут будущие исследования. Хочется верить, что законы красоты все-таки будут разгаданы, и, памятуя традиции Баха и Моцарта (см. с. 149), закончить последнюю главу об архитектуре и музыке мажорным аккордом.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'