Приближенные числа

Кто незнаком с правилами действий над приближенными числами, тому, вероятно, интересно будет хотя бы вкратце с ними ознакомиться, тем более что знание этих простых приемов оказывается и практически полезным, сберегая труд и время при вычислениях.

Объясним прежде всего, что такое приближенное число и откуда такие числа получаются.

При изготовлении литровой мерной кружки закон допускает погрешность до 5 куб. см

Данные, входящие в технические расчеты, получаются путем измерения. Но никакое измерение не может быть выполнено совершенно точно. Прежде всего уже самые меры, которыми пользуются для измерения, обычно заключают в себе погрешность. Изготовить совершенно точные метровые линейки, килограммовую гирю, литровую кружку чрезвычайно трудно, и закон допускает при их изготовлении некоторую погрешность. Например, при изготовлении метровой линейки допускается законом погрешность до 1 мм; для 10-метровой землемерной цепи или ленты - до 1 см; для килограммовой гири^* - до 1 г; для разновески в 1 г - до 0,01 г; для литровой кружки - до 5 куб. см.

^* (Помимо погрешности в гирях, закон допускает погрешность и в устройстве весов, доходящую, например, в столовых весах до 1 г на каждый килограмм отвешиваемого груза.)

Кроме того, выполнение измерения вводит еще неточности. Пусть вы измеряете какое-нибудь расстояние, например ширину улицы. Мера, метр, отложилась в ее ширине, допустим, 13 раз, и еще остался кусочек меньше метра. Вы можете сказать, что ширина улицы 13 м; на самом деле, однако, она равна 13 целым метрам и еще некоторому числу десятых, сотых и т. д. долей метра, которых вы не учли. Следовательно, результат вашего измерения можно изобразить так:

ширина улицы - 13,??? м,

где вопросительные знаки означают неизвестные нам цифры десятых, сотых и т. д. долей.

Если бы вы пожелали измерить ширину улицы точнее, вы узнали бы, сколько в остающемся кусочке содержится дециметров (десятых долей метра). Допустим, что дециметров содержится 8 и еще имеется некоторый остаток, меньший дециметра. Результат нового измерения, 13,8 м, будет точнее предыдущего, но и он не строго точен, потому что, кроме 8 десятых метра, в ширине улицы заключается еще некоторое неизвестное нам число сотых, тысячных и т. д. долей метра. Следовательно, полученный сейчас более точный результат мы можем выразить так:

13,8?? м.

При еще более тщательном измерении вы учтете сотые доли метра (сантиметры) в откинутом остатке, но пренебрежете остатком, меньшим сантиметра; значит, и этот результат не будет абсолютно точен. Вообще, как бы аккуратно вы ни мерили, никогда не можете вы быть твердо уверены, что далее последней полученной вами цифры не находятся еще другие, вам неизвестные.

Дело, конечно, нисколько не меняется от того, что при измерениях остатки, большие половины единицы меры, обычно считаются за целые. Если бы при первом измерении улицы мы считали ее ширину не 13 м, а 14, - это также был бы лишь приближенный результат. Его можно было бы выразить так:

14,??? м,

где вопросительные знаки означают отрицательные цифры (то-есть показывают, на сколько десятых, сотых и т. д. долей число 14 больше истинной ширины улицы).

Итак, результат даже самого тщательного измерения не может быть рассматриваем как совершенно точный: он выражает истинную величину лишь более или менее приближенно. Такие числа называются приближенными.

Арифметика приближенных чисел не ео всем сходна с арифметикой чисел точных. Покажем это различие на примере.

Пускай требуется вычислить площадь прямоугольного участка, длина которого 68 м, а ширина - 42 м. Если бы числа 68 и 42 были точные, площадь участка в точности равнялась бы

68 X 42 = 2856 кв. м.

Но числа 68 и 42 не точные, а приближенные: в длине не ровно 68 м, а немного больше или меньше, так как невероятно, чтобы метр укладывался в ней в точности 68 раз. Да и самая длина метровой линейки вряд ли в точности была равна 1 м. Мы можем, согласно предыдущему, выразить длину участка в метрах так:

68,?

Подобным же образом и ширину участка выразим через

42,?

Проделаем теперь умножение приближенных чисел:

68,? X 42,?

Выполнение действия видно из следующей схемы:

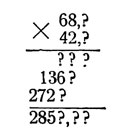
Мы видим, что четвертая цифра результата нам неизвестна: она должна получиться от сложения трех цифр (? + 6 + ?), из которых две неизвестны. Недостоверна также и третья цифра результата. Мы записали 5, но ведь от сложения столбца ? + 6 + ? могло получиться число больше 10 и даже 20; значит, вместо 5 может оказаться и 6 и 7. Вполне надежны только первые две цифры результата (28). Поэтому, желая быть добросовестными, мы должны утверждать лишь, что искомая площадь заключает около 28 сотен квадратных метров. Каковы цифры десятков и единиц в числе квадратных метров, нам неизвестно.

Итак, правильный ответ на вопрос задачи - 2800 причем ноли означают не заведомое отсутствие единиц соответствующих разрядов, а лишь отсутствие достоверных знаний о них. Ноли означают здесь то же, что и вопросительные знаки в предыдущих обозначениях.

Ошибочно думать, что ответ 2856, полученный по правилам арифметики точных чисел, вернее ответа 2800. Ничуть: ведь мы видели, что последние две цифры результата (56) доверия не заслуживают: поручиться за них нельзя. Ответ 2800 предпочтительнее, чем 2856, потому что он не вводит в заблуждение - он прямо утверждает, что достоверны лишь цифры 2 и 8 на месте тысяч и сотен, а какие цифры идут дальше - неизвестно. Ответ же 2856 обманчив: он внушает неверную мысль, будто последние две цифры столь же надежны, как и первые две.

"Нечестно писать больше цифр, чем столько, за сколько мы можем ручаться... Мне очень грустно признаться, что не мало таких чисел, ведущих к превратным представлениям, встречается в лучших сочинениях о паровых машинах... Когда я учился в школе, нам сообщали, что среднее расстояние от Земли до Солнца 95 142357 английских миль^*. Я удивляюсь, почему не было упомянуто, сколько еще футов и дюймов. Наиболее точные современные измерения позволяют лишь утверждать, что это расстояние не больше 93 и не меньше 92,5 миллиона миль", - писал по этому поводу английский математик Перри.

^* (Английская миля равна 1852 м.)

Итак, при выкладках с приближенными числами надо принимать во внимание не все цифры результата, а только некоторые. Остановимся на том, как надо округлять числа.