Глава восьмая. Математические загадки пирамиды Хеопса

Математические загадки пирамиды Хеопса

Высочайшая пирамида древнего Египта- Хеопсова, уже пять тысячелетий обвеваемая знойным воздухом пустыни, представляет без сомнения самую удивитеостройку, сохранившуюся от древнего мира. Высотой почти в 150 м, она покрывает своим основанием площадь в 40000 кв. м и сложена из 200 рядов исполинских камней. 10000 рабов в течение 30 лет трудились над возведением этого сооружения, сначала подготовляя 10 лет дорогу для перевозки камней от каменоломни до места постройки, а затем громоздя их 20 лет друг на друга с помощью несовершенных машин того времени.

Было бы странно, чтобы такое огромное сооружение воздвигнуто было с единственной целью - служить гробницей для правителя страны. Поэтому некоторые исследователи стали доискиваться: не раскроется ли тайна пирамиды из соотношения ее размеров?

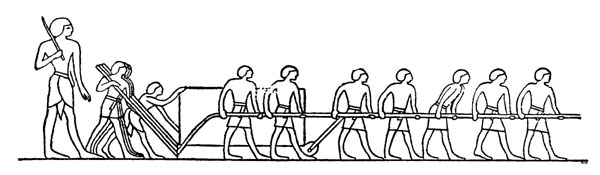
Перевозка камня на стройку пирамиды. Сзади рабочих идет надсмотрщик с хлыстом; поскольку он важнее всех остальных работников, он изображается более крупно (древнеегипетский рисунок)

Им посчастливилось, по их мнению, найти ряд удивительных соотношений, свидетельствующих о том, что жрецы, руководители работ по постройке, обладали глубокими познаниями по математике и астрономии и эти познания воплотили в каменных формах пирамиды.

"Геродот^* рассказывает,- читаем мы в книге французского астронома Море ("Загадки науки", 1926, т. 1), - что египетские жрецы открыли ему следующее соотношение между стороной основания пирамиды и ее высотой: квадрат, построенный на высоте пирамиды, в точности равен площади каждого из боковых треугольников. Это вполне подтверждается новейшими измерениями. Вот доказательство, что во все времена пирамида Хеопса рассматривалась как памятник, пропорции которого рассчитаны математически.

^* (Геродот - знаменитый греческий историк; посетил Египет за 300 лет до нашей эры.)

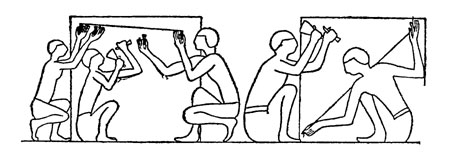
При обтесывании каменных глыб египтяне пользовались растянутым шнурком, которым выявлялись неровности на обрабатываемой поверхности. Инструментами каменотесов были металлические зубила и деревянные молотки с конической головкой. Во всех крупных египетских постройках, включая пирамиды, огромные и тяжелые глыбы тесаного камня для лучшей плотности прилегания и устойчивости клали гладкой стороной внутрь

Приведу более позднее доказательство: мы знаем, что отношение между длиной окружности и ее диаметром есть постоянная величина, хорошо известная современным школьникам. Чтобы вычислить длину окружности, достаточно умножить ее диаметр на 3,1416.

Математики древности знали это отношение лишь грубо приближенно.

Но вот, если сложить четыре стороны основания пирамиды, мы получим для ее обвода 931,22 м. Разделив же это число на удвоенную высоту (2 X 148,208), имеем в результате 3,1416, то-есть отношение длины окружности к диаметру. (Другие авторы из тех же измерений пирамиды выводят значение π с еще большей точностью: 3,14159. - Я. П.)

Этот единственный в своем роде памятник представляет собою, следовательно, материальное воплощение числа "пи", игравшего столь важную роль в истории математики. Египетские жрецы имели, как видим, точные представления по ряду вопросов, которые считаются открытиями ученых позднейших веков"^*.

^* (Значение "пи" с той точностью, которая получена здесь из соотношений размеров пирамиды, стало известно европейским математикам только в XVI веке.)

Еще удивительнее другое соотношение: если сторону основания пирамиды разделить на точную длину года - 365,2422 суток, то получается как раз 10000000-я доля земной полуоси - с точностью, которой могли бы позавидовать современные астрономы...

Далее: высота пирамиды составляет ровно миллиардную долю расстояния от Земли до Солнца - величины, которая европейской науке стала известна лишь в конце XVIII века. Египтяне 5000 лет назад знали, оказывается, то, чего не знали еще ни современники Галилея^* и Кеплера^**, ни ученые эпохи Ньютона^***. Неудивительно, что изыскания этого рода породили на Западе обширную литературу.

^* (Галилей Галилео (1564-1642) - великий итальянский физик, механик и астроном, один из основателей точного естествознания.)

^** (Кеплер Иоганн (1571-1630) - выдающийся немецкий астроном, открывший на основе учения великого польского ученого Николая Коперника законы движения.)

^*** (Ньютон Исаак (1643-1727) - величайший английский математик, астроном и физик, всю жизнь посвятивший исключительно научным занятиям.)

А между тем все это - не более как игра цифрами. Дело представится совсем в другом свете, если подойти к нему с оценкой результатов приближенных вычислений.

Рассмотрим же по порядку те примеры, которые мы привели.

1. О числе "пи". Арифметика приближенных чисел утверждает, что если в результате действия деления желаем получить число с шестью верными цифрами (3,14159), мы должны иметь в делимом и делителе по крайней мере столько же верных цифр. Это значит - в применении к пирамиде, - что для получения шестизначного "пи" надо было измерить стороны основания и высоту пирамиды с точностью до миллионных долей результата, то-есть до 1 мм. Астроном Море приводит для высоты пирамиды 148,208 м, на первый взгляд как будто действительно с точностью до 1 мм.

Но кто поручится за такую точность измерения пирамиды? Вспомним, что в лабораториях Института мер (ВИМС), где производятся точнейшие в мире измерения, не могут при измерении длины добиться такой точности (получают при измерении длины лишь шесть верных цифр). Понятно, насколько грубее может быть выполнено измерение каменной громады в пустыне. Правда, при точнейших землемерных работах (при измерении так называемых "базисов") можно и на местности достичь такой же точности, как и в лаборатории, то-есть ручаться за шесть десятичных знаков. Но, конечно, невозможно осуществить это в условиях измерения пирамиды. К тому же истинных, первоначальных размеров пирамиды давно нет в натуре, так как облицовка сооружения выветрилась, и никто не знает, какой она была толщины. Чтобы быть добросовестным, надо брать размеры пирамиды в целых метрах, а тогда получается довольно грубое "пи", не более точное, чем то, которое давно известно из математического папируса Ринда.

Если пирамида действительно есть каменное воплощение числа "пи", то воплощение это, как видим, далеко не совершенное. Но вполне допустимо, что пирамида не сооружена ради выражения именно этого соотношения. В пределы приближенных трехзначных чисел для размеров пирамиды хорошо укладываются и другие допущения. Возможно, например, что для высоты пирамиды было взято 2/3 ребра пирамиды или 2/3 диагонали ее основания. Вполне допустимо и то соотношение, которое было указано Геродотом: что высота пирамиды есть квадратный корень из площади боковой грани. Все это - догадки, столь же вероятные, как и "гипотеза пи".

2. Следующее утверждение касается продолжительности года и длины земного радиуса: если разделить сторону основания пирамиды на точную длину года (число из семи цифр), то получим в точности 10000000-ю долю земной оси (число из пяти цифр). Но раз мы уже знаем, что в делимом у нас не больше трех верных цифр, то ясно, какую цену имеют здесь эти семь и пять знаков в делителе и в частном. Арифметика может ручаться в этом случае только за три цифры в длине года и земного радиуса. Год в 365 суток и земной радиус около 6400 км - вот числа, о которых мы вправе здесь говорить.

3. Что же касается расстояния от Земли до Солнца, то здесь недоразумение иного рода. Странно даже, как приверженцы теории могут не замечать допускаемой ими здесь логической ошибки. Ведь если, как они утверждают, сторона пирамиды составляет известную долю земного радиуса, а высота - известную долю основания, то нельзя уже говорить, будто та же высота составляет определенную долю расстояния до Солнца. Что-нибудь одно - либо то, либо другое. А если случайно тут обнаруживается любопытное соответствие обеих длин, то оно всегда существовало в нашей планетной системе, и никакой заслуги жрецов в этом быть не может.

Сторонники рассматриваемой теории идут еще далее: они утверждают, что масса пирамиды составляет ровно одну тысячебиллионную долю массы земного шара. Это соотношение, по их мнению, не может быть случайным и свидетельствует о том, что древнеегипетские жрецы знали не только геометрические размеры нашей планеты, но и задолго до Ньютона и Кавендиша^* исчислили ее массу - "взвесили" земной шар.

^* (Кавендиш Генри (1731-1810) - английский физик.)

Здесь та же самая нелогичность, что и в примере с расстоянием от Земли до Солнца. Совершенно нелепо говорить о том, будто масса пирамиды "выбрана" в определенном соответствии с массой земного шара. Масса пирамиды определилась с того момента, как назначены были размеры ее основания и высоты.

Нельзя одновременно сообразовать высоту пирамиды с основанием, составляющим определенную долю земного радиуса, и независимо от этого ставить ее массу в связь с массой Земли. Одно определяется другим.

Значит, должны быть отвергнуты всякие домыслы о знании египтянами массы земного шара. Это не более как числовая эквилибристика (то-есть изворотливость. - Ред.).

Искусно оперируя с числами, опираясь на случайные совпадения, можно доказать, пожалуй, все что угодно.

Мы видим, на каких шатких основаниях покоится легенда о непостижимой учености жрецов-архитекторов пирамиды.

Попутно мы имеем тут и маленькую наглядную демонстрацию пользы того отдела арифметики, который занимается приближенными числами.