Для обиходных расчетов

Существует огромное множество приемов ускоренного выполнения арифметических действий - приемов, предназначаемых для обиходных вычислений. Составилась бы целая книга, если задаться целью описать хотя бы только главнейшие из них. Ограничусь поэтому лишь несколькими примерами из числа наиболее удобоприменимых.

В практике технических и торговых вычислений нередки случаи, когда приходится складывать столбцы чисел, близких друг к другу по величине. Например:

Точно так же находим сумму:

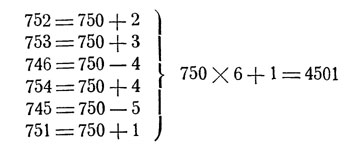
Сходным образом поступают, когда находят арифметическое среднее чисел, близких между собой по величине. Найдем, например, среднюю из следующих цен:

Отсюда искомая средняя цена

4 р. 70 к. + 1,5 к. = 4 р. 71,5 к.

Перейдем к умножению. Здесь прежде всего укажем, что умножение на числа 5, 25 и 125 значительно ускоряется, если иметь в виду следующее:

5 = 10/2; 25 = 100/4; 125 = 1000/8.

Поэтому, например,

 36 Х   5 =   360/2 =  180;   87 X   5 =   870/2 =   435; 
 36 Х  25 =  3600/4 =  900;   87 X  25 =  8700/4 =  2175; 
 36 X 125 = 36000/8 = 4500,   87 X 125 = 87000/8 = 10875.

При умножении на 15 можно пользоваться тем, что

15 = 10 Х 1 1/2.

Поэтому легко производить в уме вычисления вроде таких:

36 X 15 = 360 X 1 1/2 = 360 + 180 = 540,

или проще:

 36 X 1 1/2 X 10 = 540; 
 87 X 15 = 870 + 435 = 1305.

При умножении на 11 нет надобности писать пять строк:

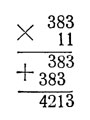
Достаточно лишь под умноженным числом подписать его еще раз, отодвинув на одну цифру:

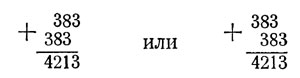
и произвести сложение.

Полезно запомнить результаты умножения первых девяти чисел на 12, 13, 14 и 15. Тогда умножение многозначных чисел на такие множители значительно ускоряется. Пусть требуется умножить

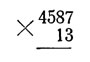
Поступаем так. Каждую цифру множимого умножаем в уме сразу на 13:

 7 X 13 = 91;                 1 пишем, 9 запоминаем; 
 8 X 13 = 104; 104 + 9 = 113; 3 пишем, 11 запоминаем; 
 5 X 13 = 65; 65 + 11 = 76;   6 пишем, 7 запоминаем; 
 4 X 13 = 52; 52 + 7 = 59. 

Итого - 59631.

После нескольких упражнений прием этот легко усваивается.

Весьма удобный прием существует для умножения двузначных чисел на 11: надо раздвинуть цифры множимого и вписать между ними их сумму:

43 Х 11 = 473.

Если же сумма цифр двузначная, то число ее десятков прибавляют к первой цифре множимого:

48 X 11 = 4(12)8, то-есть 528.

Укажем, наконец, кое-какие приемы ускоренного деления.

При делении на 5 умножают делимое и делитель на 2:

3471 : 5 = 6942 : 10 = 694,2.

При делении на 25 умножают оба числа на 4:

3471 : 25 = 13884 : 100 = 138,84.

Сходным образом поступают при делении на 1 1/2 (= 1,5) и на 2 1/2(= 2,5):

 3471 : 1 1/2 = 6942 : 3 = 2314, 
 3471 :  2,5  = 13884 : 10= 1388,4.