Глава седьмая. Быстрый счет

Приемы ускоренного умножения

Быстрый счет

Одним из приемов ускоренного умножения является прием перекрестного умножения, весьма удобный при действии с двузначными числами. Способ не нов: он восходит к грекам и индусам и в старину назывался "способом молнии" или "умножением крестиком".

Пусть требуется перемножить 24 X 32. Мысленно располагаем числа по следующей схеме, одно под другим:

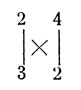
Теперь последовательно производим следующие действия:

1. 4 X 2 = 8 - это последняя цифра результата;
2. 2 X 2 = 4; 4 X 3 = 12; 4 + 12 = 16; 6 - предпоследняя цифра результата; единицу запоминаем;
3. 2 Х 3 = 6 да еще удержанная в уме единица, имеем 7 - это первая цифра результата.

Получаем все цифры произведения: 7, 6, 8 - 768.

После непродолжительного упражнения прием этот усваивается очень легко.

Другой способ, состоящий в употреблении так называемых "дополнений", удобно применяется в тех случаях, когда перемножаемые числа близки к 100.

Предположим, что требуется перемножить 92X96. "Дополнение" для 92 до 100 будет 8, для 96 - 4. Действие производят по следующей схеме:

 множители: 92 и 96, 
 дополнения: 8 и  4.

Первые две цифры результата получаются простым вычитанием из множителя "дополнения" множимого или наоборот: то-есть из 92 вычитают 4 или из 96 - 8. В том и другом случае имеем 88; к этому числу приписывают произведение "дополнений": 8 X 4 = 32. Получаем результат 8832.

Что полученный результат должен быть верен, наглядно видно из следующих преобразований:

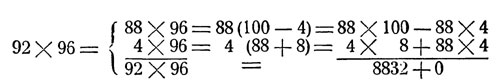
Еще пример - требуется перемножить 78 на 77:

 множители:  78 и 77, 
 дополнения: 22 и 23. 
 78   - 23  =  55, 
 22   Х 23  = 506, 
 5500 + 506 = 6006.