Числовые пирамиды

В следующих витринах галереи нас поражают числовые достопримечательности совсем особого рода - некоторое подобие пирамид, составленных из чисел, Рассмотрим поближе первую из них:

        1 X 9 + 2 = 11 
       12 X 9 + 3 = 111 
      123 X 9 + 4 = 1111 
     1234 X 9 + 5 = 11111 
    12345 X 9 + 6 = 111111 
   123456 X 9 + 7 = 1111111 
  1234567 X 9 + 8 = 11111111 
 12345678 X 9 + 9 = 111111111 

Как объяснить эти своеобразные результаты умножения?

Чтобы постичь эту странную закономерность, возьмем для примера какой-нибудь из средних рядов нашей числовой пирамиды: 123456 X 9 + 7. Вместо умножения на 9 можно умножить на (10 - 1), то-есть приписать 0 и вычесть умножаемое:

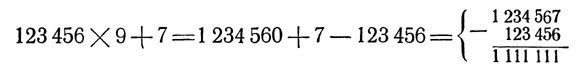
Достаточно взглянуть на последнее вычитание, чтобы понять, почему тут получается результат, состоящий только из одних единиц.

Мы можем уяснить себе это, исходя и из других рассуждений. Чтобы число вида 12345... превратилось в число вида 11111..., нужно из второй его цифры вычесть 1, из третьей - 2, из четвертой - 3, из пятой - 4 и т. д. - иначе говоря, вычесть из него то же число вида 12345..., вдесятеро уменьшенное и предварительно лишенное последней цифры. Теперь понятно, что для получения искомого результата нужно наше число умножить на 10, прибавить к нему следующую за последней цифру и вычесть из результата первоначальное число (а умножить на 10 и отнять множимое - значит умножить на 9).

Сходным образом объясняется образование и следующей числовой пирамиды, получающейся при умножении определенного ряда цифр на 8 и прибавлении последовательно возрастающих цифр:

         1 X 8 + 1 = 9 
        12 X 8 + 2 = 98 
       123 X 8 + 3 = 987 
      1234 X 8 + 4 = 9876 
     12345 X 8 + 5 = 98765 
    123456 X 8 + 6 = 987654 
   1234567 X 8 + 7 = 9876543 
  12345678 X 8 + 8 = 98765432 
 123456789 X 8 + 9 = 987654321 

Особенно интересна в пирамиде последняя строка, где в результате умножения на 8 и прибавления 9 происходит превращение натурального ряда цифр в таковой же ряд, но с обратным расположением. Объясним эту особенность.

Получение странных результатов уясняется из следующей строки:

¹ (Почему 12345 X 9 + 6 дает именно 111111, было показано при рассмотрении предыдущей числовой пирамиды.)

то-есть 12345 X 8 + 5 = 111111 - 12346. Но, вычитая из числа 111111 число 12346, составленное из ряда возрастающих цифр, мы, как легко понять, должны получить ряд убывающих цифр: 98765.

Вот наконец третья числовая пирамида, также требующая объяснения:

        9 X 9 + 7 = 88 
       98 X 9 + 6 = 888 
      987 X 9 + 5 = 8888 
     9876 X 9 + 4 = 88888 
    98765 X 9 + 3 = 888888 
   987654 X 9 + 2 = 8888888 
  9876543 X 9 + 1 = 88888888 
 98765432 X 9 + 0 = 888888888 

Эта пирамида является прямым следствием первых двух. Связь устанавливается очень легко. Из первой пирамиды мы знаем уже, что, например:

12345 X 9 + 6 = 111111.

Умножив обе части на 8, имеем:

(12345 X 8 X 9) + (6 X 8) = 888 888.

Но из второй пирамиды известно, что

12345 X 8 + 5 = 98765, или 12345 X 8 = 98760. 

Значит:

888888 = (12345 X 8 X 9) + (6 X 8) = (98760 X 9) + 48 = (98760 Х 9) + (5 Х 9) + 3 = (98760 + 5) Х 9+ 3 = 98765 X 9 + 3.

Вы убеждаетесь, что все эти числовые пирамиды не так уж загадочны, как кажутся с первого взгляда.