Простейшая система счисления

Нетрудно сообразить, что в каждой системе высшая цифра, какая может понадобиться, равна основанию этой системы без единицы. Например, в десятичной системе высшая цифра 9, в шестеричной - 5, в троичной - 2, в пятнадцатеричной - 14 и т. д.

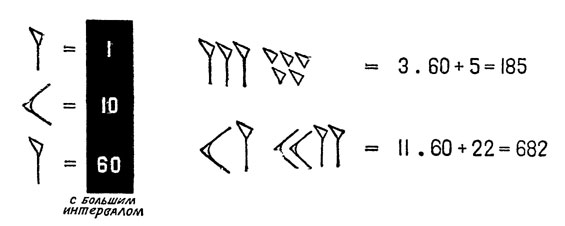
Клинописные цифры вавилонской шестидесятеричной системы. Для записи целых чисел вавилоняне пользовались всего двумя знаками - 1 и 10; 60 изображалось знаком единицы, но с большим интервалом от следующих цифр

Самая простая система счисления, конечно, та, для которой требуется меньше всего цифр. В десятичной системе нужны десять цифр (считая и 0), в пятеричной - пять цифр, в троичной - три цифры (1, 2 и 0), в двоичной - только две цифры (1 и 0).

Существует ли и "единичная" система? Конечно, - это система, в которой единицы высшего разряда в один раз больше единицы низшего, то-есть равны ей; другими словами, "единичной" можно назвать такую систему, в которой единицы всех разрядов имеют одинаковое значение. Это самая примитивная "система"; ею пользовался первобытный человек, делая на дереве зарубки по числу сосчитываемых предметов. Но между нею и всеми другими системами счета есть громадная разница: она лишена главного преимущества нашей нумерации - так называемого поместного значения цифр. Действительно: в "единичной" системе знак, стоящий на третьем или пятом месте, имеет то же значение, что и стоящий на первом месте. Между тем даже в двоичной системе единица на третьем месте (справа) уже в 4 раза (2 X 2) больше, чем на первом, а на пятом - в 16 раз больше (2 X 2 X 2 X 2). Для изображения какого-нибудь числа по "единичной" системе нужно ровно столько же знаков, сколько было сосчитано предметов: чтобы записать сто предметов, нужно сто знаков, в двоичной же - только семь ("1100100"), а в пятеричной - всего три ("400").

Вот почему "единичную" систему едва ли можно назвать "системой"; по крайней мере, ее нельзя поставить рядом с остальными, так как она принципиально от них отличается, не давая никакой экономии в изображении чисел. Если же ее откинуть, то простейшей системой счисления нужно признать систему двоичную, в которой употребляются всего две цифры: 1 и 0. При помощи единицы и нуля можно изобразить все бесконечное множество чисел. На практике система эта мало удобна - получаются слишком длинные числа^*; но теоретически она имеет все права считаться простейшей. Она обладает некоторыми любопытными особенностями, присущими только ей одной; особенностями этими, между прочим, можно воспользоваться для выполнения ряда эффектных математических фокусов, о которых мы скоро побеседуем подробно в главе "Фокусы без обмана".

^* (Зато, как увидим далее, для такой системы до крайности упрощаются таблица сложения и таблица умножения.)