Глава четвертая. Недесятичные системы счисления

Недесятичные системы счисления

Эту главу позволю себе начать с задачи, которую я придумал когда-то для читателей старого распространенного журнала^* в качестве "задачи на премию".

^* ("Природа и люди" (потом она была перепечатана в сборнике Е. И. Игнатьева "В царстве смекалки").)

Вот она:

"Загадочная автобиография

В бумагах одного чудака-математика найдена была его автобиография. Она начиналась следующими строками:

"Я окончил курс университета 44 лет от роду. Спустя год, 100-летним молодым человеком, я женился на 34-летней девушке. Незначительная разница в возрасте - всего 11 лет - способствовала тому, что мы жили общими интересами и мечтами. Спустя немного лет у меня была уже и маленькая семья из 10 детей. Жалованья я получал в месяц всего 200 руб., из которых 1/l0 приходилось отдавать сестре, так что мы с детьми жили на 130 руб. в месяц" и т. д.

Чем объяснить странные противоречия в числах этого отрывка?"

Решение задачи подсказывается названием этой главы: недесятичная система счисления - вот единственная причина кажущейся противоречивости приведенных чисел. Напав на эту мысль, нетрудно догадаться, в какой именно системе счисления изображены числа чудаком-математиком. Секрет выдается фразой: "спустя год (после 44 лет), 100-летним молодым человеком..." Если от прибавления одной единицы число 44 преображается в 100, то, значит, цифра 4 - наибольшая в этой системе (как 9 - в десятичной), а следовательно, основанием системы является 5. Чудаку-математику пришла фантазия написать все числа своей биографии по пятеричной системе счисления, то-есть по такой, в которой единица высшего разряда не в 10, а в 5 раз больше единицы низшего; на первом справа месте стоят в ней простые единицы (не свыше четырех), на втором - не десятки, а пятерки; на третьем - не сотни, а "двадцатипятерки" и т. д. Поэтому число, изображенное в тексте записки "44", означает не 4 X 10 + 4, как в десятичной системе, а 4 X 5 + 4, то-есть 24.

Точно так же число "100" в автобиографии означает одну единицу третьего разряда в пятеричной системе, то-есть 25. Остальные числа записки соответственно означают:

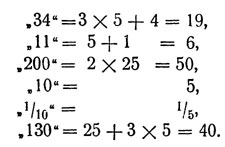
Восстановив истинный смысл чисел записки, мы видим, что в ней никаких противоречий нет:

Я окончил курс университета 24 лет от роду. Спустя год, 25-летним молодым человеком, я женился на 19-летней девушке. Незначительная разни-ца в возрасте - всего 6 лет - способствовала тому, что мы жили общими интересами и мечтами. Спустя немного лет у меня была уже и маленькая семья из 5 детей. Жалованья я получал в месяц 50 руб., из которых 1/5 приходилось отдавать сестре, так что мы с детьми жили на 40 руб. в месяц.

Трудно ли изображать числа в других системах счисления? Нисколько. Положим, вы желаете число 119 изобразить в пятеричной системе. Делите 119 на 5, чтобы узнать, сколько в нем единиц первого разряда:

119 : 5 = 23, остаток 4.

Значит, число простых единиц будет 4. Далее, 23 пятерки не могут стоять все во втором разряде, так как высшая цифра в пятеричной системе - 4, и больше 4 единиц ни в одном разряде быть не должно. Делим поэтому 23 на 5:

23 : 5 = 4, остаток 3.

Это показывает, что во втором разряде (пятерок) будет цифра 3, а в третьем ("двадцатипятерок") - 4.

Итак, 119 = 4 X 25 + 3 X 5 + 4, или в пятеричной системе "434".

Сделанные действия для удобства располагают так:

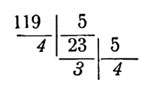
Курсивные цифры (при письме можно их подчеркивать) выписывают справа налево и сразу получают искомое изображение числа в иной системе.

Приведем еще примеры.

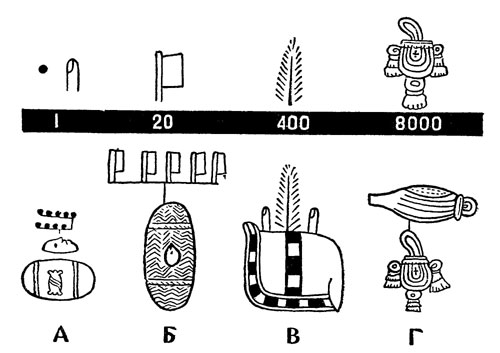
Числовая система ацтеков Мексики была двадцатеричной. Количества до 20 они изображали числом точек или пальцев; для 20 рисовался флаг; число 400 (20 X 20) имело значок, похожий на ель, который значил - 'многочисленный, как волосы'. Для самой большой единицы счета - 8000 (20 X 20 X 20) - изображался мешок: он символизировал огромное количество бобов какао в мешке. Чтобы изобразить некоторое количество предметов, ацтеки прямо пририсовывали к изображению этого предмета нужные числовые значки: таким образом, А означает 9 масок из драгоценного камня; Б - 100 мешков какао; В - 402 бумажных одеяла указанного рисунка; Г - 8000 связок листьев копаловой камеди

Пример 1.

Изобразить 47 в троичной системе:

Решение:

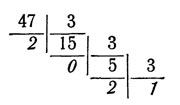
Ответ: "1202". Проверка: 1 X 27 + 2 X 9 + 0 X 3 + + 2 = 47.

Пример 2.

Число 200 изобразить в семеричной системе.

Решение:

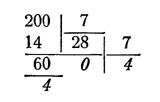
Ответ: "404". Проверка: 4 X 49 + 0 X 7 + 4 = 200.

Пример 3.

Число 163 изобразить в двенадцатеричной системе.

Решение:

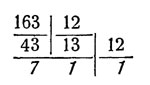
Ответ: "117". Проверка: 1 X 144 + 1 X 12 + 7 = 163

Теперь читатель не затруднится изобразить любое число в какой угодно системе счисления. Единственная помеха может возникнуть лишь вследствие того, что в некоторых случаях не будет доставать обозначений для цифр. В самом деле: при изображении числа в системах с основанием более десяти (например, двенадцатеричной), может явиться надобность в цифрах

"десять" и "одиннадцать". Из этого затруднения нетрудно выйти, избрав для новых цифр какие-нибудь условные знаки или буквы - хотя бы, например, буквы К и Л.

Так, число 1579 в двенадцатеричной системе изобразится следующим образом:

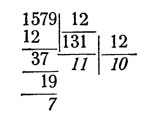
Ответ: "(10)(11)7", или КЛ7. Проверка: 10 X 144 + 11 X 12 + 7 = 1579.

Выразите:

1) Число 1926 в двенадцатеричной системе.

2) Число 273 в двадцатеричной системе.

Ответы.

1) 1146.

2) НН, где через Н обозначена цифра "13".